Sets as lists¶
As an unashamed excuse for writing structurally recursive procedures over lists, let us represent a finite set as the proper list of its elements, without repetition, in order to program Scheme procedures implementing elementary set operations: union, intersection, difference, etc.
Resources¶
- The Scheme code for the present lecture note (latest version: 15 Sep 2025).
- The Scheme code for the present lecture note with cond-expressions (latest version: 15 Sep 2025).
A practical consideration¶
The order of elements does not matter, but in practice if the elements are ordered, it simplifies things to represent a set as the sorted list of its elements.
Well-formed representation¶
A list represents a set if all of its elements only occur once:
(define positive-test-set?
(lambda (candidate)
(and (equal? (candidate '()) #t)
(equal? (candidate '(1 2 3)) #t)
;;; etc.
)))
(define negative-test-set?
(lambda (candidate)
(and (equal? (candidate '(1 2 1 3)) #f)
;;; etc.
)))
In Scheme:
(define set?
(lambda (v)
(if (null? v)
#t
(if (pair? v)
(if (member? (car v) (cdr v))
#f
(set? (cdr v)))
(errorf 'set?
"not a proper list: ~s"
v)))))
This definition passes the unit tests:
> (positive-test-set? set?)
#t
> (negative-test-set? set?)
#t
>
Set membership¶
An element belongs to a set whenever its representation occurs in the representation of this set:
(define belongs-to?
(lambda (e es)
(member? e es)))
So if e denote an element e and es the representation of a set s, evaluating (belongs-to? e es) yields #t whenever e belongs to s, and otherwise, it yields #f.
Set inclusion¶
A set is included into another set whenever each of its elements belongs to this other set:
(define positive-test-included-in?
(lambda (candidate)
(and (equal? (candidate '() '()) #t)
(equal? (candidate '() '(x)) #t)
(equal? (candidate '() '(x y z)) #t)
(equal? (candidate '(y) '(x y z)) #t)
;;; etc.
)))
(define negative-test-included-in?
(lambda (candidate)
(and (equal? (candidate '(x) '()) #f)
(equal? (candidate '(x y) '(x)) #f)
;;; etc.
)))
In the negative test, y does not belong to the set represented by (x).
Set inclusion is defined following the inductive structure of lists:
- base case: the empty set is included in all sets
- induction case:
given an element e and two sets esp and e2s
such that esp is included in e2s,
- if e belongs to e2s, then (cons e esp) is included in e2s
- if e does not belong to e2s, then (cons e esp) is not included in e2s
In Scheme:
(define included-in?
(lambda (e1s_init e2s_init)
(letrec ([traverse (lambda (e1s)
(if (null? e1s)
#t
(if (pair? e1s)
(if (belongs-to? (car e1s) e2s_init)
(traverse (cdr e1s))
#f)
(errorf 'included-in?
"not a proper list: ~s"
e1s))))])
(traverse e1s_init))))
This definition passes the unit tests:
> (positive-test-included-in? included-in?)
#t
> (negative-test-included-in? included-in?)
#t
>
So if e1s and e2s denote the representation of two sets e1s and e2s, evaluating (included-in? e1s e2s) yields #t whenever e1s is included in e2s, and otherwise, it yields #f.
It is simple to define the converse function:
(define includes?
(lambda (e2s e1s)
(included-in? e1s e2s)))
Set equality¶
We simply define set equality as mutual set inclusion:
(define set-equal?
(lambda (e1s e2s)
(and (included-in? e1s e2s)
(included-in? e2s e1s))))
Set union¶
The goal of this section is implement the traditional set union over the representations of sets.
Pictorially, given the two sets A and B,

and

that overlap like this,
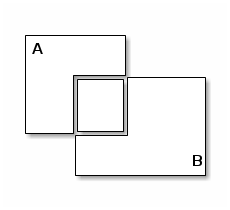
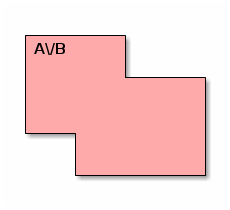
we want to compute their union, i.e., the following set:
To this end, let us first implement a predicate set-union? that is passed
- the representation of a first set, e1s,
- the representation of a second set, e2s,
- the putative representation of their union, e1s_union_e2s,
and that checks whether e1s_union_e2s indeed represents the union of the sets represented by e1s and e2s:
(define positive-test-set-union?
(lambda (candidate)
(and (equal? (candidate '() '() '()) #t)
(equal? (candidate '() '(0 1 2 3 4 5) '(0 1 2 3 4 5)) #t)
(equal? (candidate '(0 1 2 3 4 5) '() '(0 1 2 3 4 5)) #t)
(equal? (candidate '(1 2 3 4) '(0 4 5) '(0 1 2 3 4 5)) #t)
(equal? (candidate '(0 1 2 3 4 5) '(0 1 2 3 4 5) '(0 1 2 3 4 5)) #t)
(equal? (candidate '(0 1 2 3 4) '(1 2 3 4 5) '(0 1 2 3 4 5)) #t)
;;; etc.
)))
(define negative-test-set-union?
(lambda (candidate)
(and (equal? (candidate '() '() '(0)) #f)
(equal? (candidate '(0 1 2) '(4 5) '(0 1 2 3 4 5)) #f)
(equal? (candidate '(0 1 2 3 4 5) '() '(0 1 2 3 4 5 6)) #f)
(equal? (candidate '(0 1 2 6) '(3 4 5) '(0 1 2 3 4 5)) #f)
(equal? (candidate '(0 1 2 3 4) '(1 2 3 4 5) '(0 1 2 3 4 5 6)) #f)
;;; etc.
)))
The predicate is in two parts:
- Soundness: for any set A and B, each of A and B should be included in the union of A and B.
- Completeness: for any set A and B, any element e belonging to the union of A and B should belong either to A or to B.
(You can reflect on this soundness and completeness over the following particular cases:
- A and B are empty,
- A is empty but not B,
- B is empty but not A,
- A and B are not empty and they are disjoint,
- A and B are the same non-empty set, and
- A and B are not empty, not disjoint, and not the same.
These cases are exhaustive, and the last one is depicted above.)
In Scheme:
(define set-union?
(lambda (e1s e2s e1s_union_e2s)
(let ([sound
(lambda ()
;;; each element of each set belongs to the union
(and (included-in? e1s e1s_union_e2s)
(included-in? e2s e1s_union_e2s)))]
[complete
(lambda ()
;;; each element of the union belongs to either set (or both)
(letrec ([traverse
(lambda (es)
(if (null? es)
#t
(if (pair? es)
(if (or (belongs-to? (car es) e1s)
(belongs-to? (car es) e2s))
(traverse (cdr es))
#f)
(errorf 'set-union?
"not a proper list: ~s"
es))))])
(traverse e1s_union_e2s)))])
(and (sound)
(complete)))))
This definition passes the unit tests:
> (positive-test-set-union? set-union?)
#t
> (negative-test-set-union? set-union?)
#t
>
Exercise 10¶
Program a procedure set-union such that if e1s and e2s denote the representation of two sets e1s and e2s, evaluating (set-union e1s e2s) yields the representation of the union of e1s and e2s.
Friendly help:
you can use positive-test-set-union? and negative-test-set-union? to check that your union of each two sets to test is set-equal to each tested union:
(positive-test-set-union? (lambda (e1s e2s e1s_union_e2s) (set-equal? (set-union e1s e2s) e1s_union_e2s))) (negative-test-set-union? (lambda (e1s e2s e1s_union_e2s) (set-equal? (set-union e1s e2s) e1s_union_e2s)))
you can use positive-test-set-union? to test your union function in each of the unit tests:
(positive-test-set-union? (lambda (e1s e2s e1s_union_e2s) (set-union? e1s e2s (set-union e1s e2s))))
Set intersection¶
The goal of this section is implement the traditional set intersection over the representations of sets.
Pictorially, given the same two sets A and B,

and

that overlap like this,

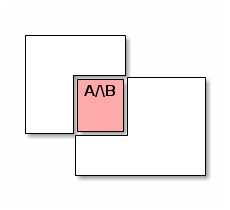
we want to compute their intersection, i.e., the following set:
To this end, let us first implement a predicate set-intersection? that is passed
- the representation of a first set, e1s,
- the representation of a second set, e2s,
- the putative representation of their intersection, e1s_inter_e2s,
and that checks whether e1s_inter_e2s indeed represents the intersection of the sets represented by e1s and e2s:
(define positive-test-set-intersection?
(lambda (candidate)
(and (equal? (candidate '() '() '()) #t)
(equal? (candidate '() '(0 1 2 3 4 5) '()) #t)
(equal? (candidate '(0 1 2 3 4 5) '() '()) #t)
(equal? (candidate '(1 2 3) '(0 4 5) '()) #t)
(equal? (candidate '(0 1 2 3 4 5) '(0 1 2 3 4 5) '(0 1 2 3 4 5)) #t)
(equal? (candidate '(0 1 2 3) '(2 3 4 5) '(2 3)) #t)
;;; etc.
)))
(define negative-test-set-intersection?
(lambda (candidate)
(and (equal? (candidate '(0 1 2 3) '(2 3 4 5) '(2 3 6)) #f)
(equal? (candidate '(0 1 2 3) '(2 3 4 5) '(2)) #f)
;;; etc.
)))
The predicate is in two parts:
- Soundness: for any set A and B, the intersection of A and B should be included both in A and in B.
- Completeness: for any set A and B, each element of A that belongs to B should belong to the intersection of A and B, and each element of B that belongs to A should belong to the intersection of A and B.
(You can reflect on this soundness and completeness over the following particular cases:
- A and B are empty,
- A is empty but not B,
- B is empty but not A,
- A and B are not empty and they are disjoint,
- A and B are the same non-empty set, and
- A and B are not empty, not disjoint, and not the same.
These cases are exhaustive, and the last one is depicted above.)
In Scheme:
(define set-intersection?
(lambda (e1s e2s e1s_inter_e2s)
(let ([sound
(lambda ()
;;; each element of the intersection belongs to both sets
(letrec ([waltz-through
(lambda (es)
(if (null? es)
#t
(if (pair? es)
(if (and (belongs-to? (car es) e1s)
(belongs-to? (car es) e1s))
(waltz-through (cdr es))
#f)
(errorf 'set-intersection?
"not a proper list: ~s"
es))))])
(waltz-through e1s_inter_e2s)))]
[complete
(lambda ()
;;; each element of one set that occurs in the other set
;;; also occurs in the intersection
(let ([relative
(lambda (es other-es)
(letrec ([run-through
(lambda (es)
(if (null? es)
#t
(if (pair? es)
(if (belongs-to? (car es) other-es)
(if (belongs-to? (car es) e1s_inter_e2s)
(run-through (cdr es))
#f)
(run-through (cdr es)))
(errorf 'set-intersection?
"not a proper list: ~s"
es))))])
(run-through es)))])
(and (relative e1s e2s) (relative e2s e1s))))])
(and (sound)
(complete)))))
This definition passes the unit tests:
> (positive-test-set-intersection? set-intersection?)
#t
> (negative-test-set-intersection? set-intersection?)
#t
>
Exercise 11¶
Program a function set-intersection such that if e1s and e2s denote the representation of two sets e1s and e2s, evaluating (set-intersection e1s e2s) yields the representation of the intersection of e1s and e2s.
Friendly help:
you can use positive-test-set-intersection? and negative-test-set-intersection? to check that your intersection of each two sets to test is set-equal to each tested intersection:
(positive-test-set-intersection? (lambda (e1s e2s e1s_inter_e2s) (set-equal? (set-intersection e1s e2s) e1s_inter_e2s))) (negative-test-set-intersection? (lambda (e1s e2s e1s_inter_e2s) (set-equal? (set-intersection e1s e2s) e1s_inter_e2s)))
you can use positive-test-set-intersection? to test your intersection function in each of the unit tests:
(positive-test-set-intersection? (lambda (e1s e2s e1s_inter_e2s) (set-intersection? e1s e2s (set-intersection e1s e2s))))
Set difference¶
The goal of this section is implement the traditional set difference over the representations of sets.
Again, given the same two sets A and B,

and

that overlap like this,

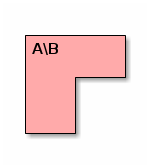
we want to compute their difference, i.e., the following set:
To this end, let us first implement a predicate set-minus? that is passed
- the representation of a first set, e1s,
- the representation of a second set, e2s,
- the putative representation of their difference, e1s_minus_e2s,
and that checks whether e1s_minus_e2s indeed represents the difference between the sets represented by e1s and e2s:
(define positive-test-set-minus?
(lambda (candidate)
(and (equal? (candidate '() '() '()) #t)
(equal? (candidate '() '(0 1 2 3 4 5) '()) #t)
(equal? (candidate '(0 1 2 3 4 5) '() '(0 1 2 3 4 5)) #t)
(equal? (candidate '(1 2 3) '(0 4 5) '(1 2 3)) #t)
(equal? (candidate '(0 1 2 3 4 5) '(0 1 2 3 4 5) '()) #t)
(equal? (candidate '(0 1 2 3) '(2 3 4 5) '(0 1)) #t)
;;; etc.
)))
(define negative-test-set-minus?
(lambda (candidate)
(and (equal? (candidate '(0 1 2 3) '(2 3 4 5) '(0 1 2)) #f)
(equal? (candidate '(0 1 2 3) '(2 3 4 5) '(0 1 4)) #f)
(equal? (candidate '(0 1 2 3) '(2 3 4 5) '(0 1 6)) #f)
;;; etc.
)))
The predicate is in two parts:
- Soundness: for any set A and B, any element in A minus B should belong to A and not to B.
- Completeness: for any set A and B, each element of B should not belong to A minus B, and for each element of A, if it belongs to B then it should not belong to A minus B, whereas if it belongs to A then it should belong to A minus B.
(You can reflect on this soundness and completeness over the following particular cases:
- A and B are empty,
- A is empty but not B,
- B is empty but not A,
- A and B are not empty and they are disjoint,
- A and B are the same non-empty set, and
- A and B are not empty, not disjoint, and not the same.
These cases are exhaustive, and the last one is depicted above.)
In Scheme:
(define set-minus?
(lambda (e1s e2s e1s_minus_e2s)
(let ([sound
(lambda ()
;;; each element of the difference belongs to the first set but not the second
(letrec ([cross
(lambda (es)
(if (null? es)
#t
(if (pair? es)
(and (and (belongs-to? (car es) e1s)
(not (belongs-to? (car es) e2s)))
(cross (cdr es)))
(errorf 'set-minus?
"not a proper list: ~s"
es))))])
(cross e1s_minus_e2s)))]
[complete
(lambda ()
;;; each element of the second set does not belong to the difference,
;;; and
;;; for each element of the first set,
;;; if it belongs to the second, it does not belong in the difference
;;; and
;;; if it does not belong to the second, it belongs to the difference
(letrec ([about-the-second-set
(lambda (es)
(if (null? es)
#t
(if (pair? es)
(if (belongs-to? (car es) e1s_minus_e2s)
#f
(about-the-second-set (cdr es)))
(errorf 'set-minus?
"not a proper list: ~s"
es))))]
[about-the-first-set
(lambda (es)
(if (null? es)
#t
(if (pair? es)
(and (if (belongs-to? (car es) e2s)
(not (belongs-to? (car es) e1s_minus_e2s))
(belongs-to? (car es) e1s_minus_e2s))
(about-the-first-set (cdr es)))
(errorf 'set-minus?
"not a proper list: ~s"
es))))])
(and (about-the-second-set e2s)
(about-the-first-set e1s))))])
(and (sound)
(complete)))))
This definition passes the unit tests:
> (positive-test-set-minus? set-minus?)
#t
> (negative-test-set-minus? set-minus?)
#t
>
Exercise 12¶
Program a function set-minus such that if e1s and e2s denote the representation of two sets e1s and e2s, evaluating (set-minus e1s e2s) yields the representation of the difference between e1s and e2s.
Friendly help:
you can use positive-test-set-minus? and negative-test-set-minus? to check that your difference of each two sets to test is set-equal to each tested difference:
(positive-test-set-minus? (lambda (e1s e2s e1s_minus_e2s) (set-equal? (set-minus e1s e2s) e1s_minus_e2s))) (negative-test-set-minus? (lambda (e1s e2s e1s_minus_e2s) (set-equal? (set-minus e1s e2s) e1s_minus_e2s)))
you can use positive_test_is_set_minus to test your minus function in each of the unit tests:
(positive-test-set-minus? (lambda (e1s e2s e1s_minus_e2s) (set-minus? e1s e2s (set-minus e1s e2s))))
Exercise 13¶
Use set-theoretic identities such as for any sets A and B,
- the intersection of [the union of A and B] and A is A,
- the intersection of [the union of A and B] and B is B,
- the difference between A and B is included in A,
- the intersection between [the difference between A and B] and B is empty,
- etc.
to beef up the unit tests above.
Exercise 14¶
Implement the traditional symmetric difference over the representations of sets.
Normalizing a list into the representation of a set¶
Since a list represents a set when it contains no repeated element, it is simple to normalize a list so that it represents a set: just remove its repeated elements.
The unit test is simple to write:
(define test-normalize-list-into-set
(lambda (candidate)
(and (set? (candidate '(1 2 3 4)))
(set? (candidate '(1 1 1 1)))
(set? (candidate '()))
(set? (candidate '(1 2 3 4 3 2 1)))
;;; etc.
)))
Normalization is defined following the inductive structure of lists:
- base case: the empty list is well formed (and represents the empty set)
- induction case:
given an element v and a list vsp that represents a set,
- if v occurs in vsp, (cons v vsp) does not represent a set (but vsp does)
- if v does not occur in vsp, (cons v vsp) represents a set
In Scheme:
(define normalize-list-into-set
(lambda (vs)
(if (null? vs)
'()
(if (pair? vs)
(let ([vsp (normalize-list-into-set (cdr vs))])
(if (member? (car vs) vsp)
vsp
(cons (car vs) vsp)))
(errorf 'normalize-list-into-set
"not a proper list: ~s"
vs)))))
This definition passes the unit test:
> (test-normalize-list-into-set normalize-list-into-set)
#t
>
Exercise 15¶
Consider the following implementation of set union:
(define set-union_quick-and-dirty
(lambda (e1s e2s)
(normalize-list-into-set (append e1s e2s))))
Do you think that this procedure does the job? Does it pass the unit tests, for example? What do you make of that?
Exercise 16¶
As is well known, your friendly Nordic deity, Loki, lives and breathes outside the box. This morning, he suggested the following radical implementation of set union:
(define set-union_outside-the-box
(lambda (e1s e2s)
(append e1s e2s)))
Do you think that this procedure does the job? Does it pass the unit tests, for example? What do you make of that?
Resources¶
- The Scheme code for the present lecture note (latest version: 15 Sep 2025).
- The Scheme code for the present lecture note with cond-expressions (latest version: 15 Sep 2025).
Version¶
Fixed a typo in the two resource files, thanks to Mansansala Eugenio Batista’s eagle eye [15 Sep 2025]
Created [11 Sep 2025]