The Scheme programming language, continued further¶
See also
Goal¶
This chapter further introduces the Scheme programming language.
Resources¶
- The Scheme code for the present lecture note (latest version: 11 Sep 2025).
Core special form: letrec¶
- <letrec-expression> ::= (letrec <letrec-header> <letrec-body>)
- <letrec-body> ::= <expression>
- <letrec-header> ::= ({<letrec-binding>}*)
- <letrec-binding> ::= [<variable> <letrec-definiens>]
- <letrec-definiens> ::= <lambda-abstraction>
Note: in most other dialects of Scheme, letrec-bindings are not delimited with square brackets by default but with ordinary parentheses.
A letrec-expression also looks like a let-expression. It has a header (a number of clauses – the letrec-bindings – possibly zero) and a body (an expression). In the header of a letrec-expression, each clause consists of a variable and a definiens, which is a lambda-abstraction. All the variables declared in a letrec-expression must be distinct.
When a letrec-expression is evaluated, the letrec-definiens are evaluated to mutually recursive procedures, each name is bound to the corresponding procedure, and the resulting bindings extend the current environment, in addition to the current bindings. Evaluating the letrec-expression then reduces to evaluating its body in this extended environment.
For example, let us revisit the addition procedure:
(define add_revisited
(lambda (n1 n2)
(letrec ([visit (lambda (n1 n2)
(if (= n1 0)
n2
(+ 1 (visit (- n1 1) n2))))])
(visit n1 n2))))
Procedure add_revisited is globally defined with a local procedure visit that is structurally recursive. And it passes the unit test from last week too:
> (unit-tests-for-add add_revisited)
#t
>
Graphically:
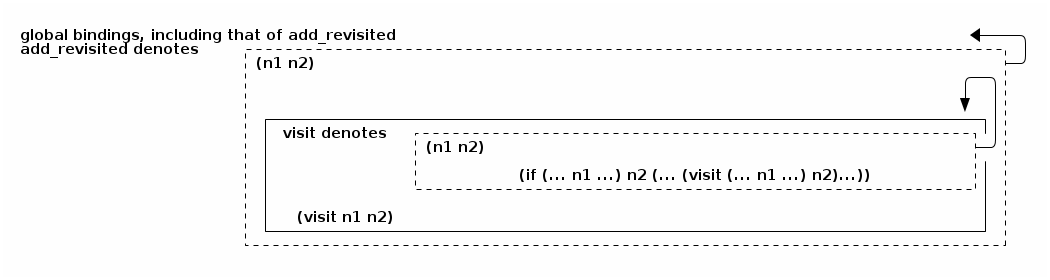
- The expression (visit n1 n2), i.e., the initial call to
visit, is evaluated in an environment
where
- visit denotes a dyadic procedure (the inner dashed box just above) whose lexical scope (the arrow exiting the inner dashed box) contains its recursive binding (the arrow is circular, and so visit can refer to itself) and where
- n1 and n2 denote the actual parameters of the anonymous procedure denoted by add_revisited (the outer dashed box just above), which is bound in the global environment.
- The expression (visit (- n1 1) n2), i.e., the recursive call to
visit, is evaluated in an environment
where
- n1 and n2 denote the actual parameters of the recursive procedure denoted by visit,
- visit is bound recursively, and where
- - denotes the predefined procedure that subtracts its second argument from its first argument.
In the local definition, instead of passing n2 again and again to visit, we can instead not pass it at all and let n2 refer to the formal parameter of the top-most lambda-abstraction:
(define add_revisited_alt
(lambda (n1 n2)
(letrec ([visit (lambda (n1)
(if (= n1 0)
n2
(+ 1 (visit (- n1 1)))))])
(visit n1))))
And it passes the unit test too:
> (unit-tests-for-add add_revisited_alt)
#t
>
Graphically:

The expression (visit n1), i.e., the initial call to visit, is evaluated in an environment where
visit denotes a monadic procedure (the inner dashed box just above) whose lexical scope (the arrow exiting the inner dashed box) contains
- its recursive binding (the arrow is circular, and so visit can refer to itself) and
- the binding of n2 to the second actual parameter of the anonymous procedure denoted by add_revisited_alt (the outer dashed box just above), which is bound in the global environment,
and where
n1 denotes the first actual parameter of the anonymous procedure denoted by add_revisited_alt.
The expression (visit (- n1 1)), i.e., the recursive call to visit, is evaluated in an environment where
- n1 denotes the actual parameter of the recursive procedure denoted by visit,
- visit is bound recursively,
- n2 denotes the second actual parameter of the anonymous procedure denoted by add_revisited_alt, and where
- - denotes the predefined procedure that subtracts its second argument from its first argument.
Exercise AA¶
In this exercise,
you are asked to trace the letrec-declared lambda-abstraction in the definitions of add_revisited and add_revisited_alt and to compare what is printed when evaluating, say, (add_revisited 3 5) and (add_revisited_alt 3 5). See how in one case visit has two arguments (and the second one remains the same throughout the calls), and how in the other case visit has one argument?
Procedure add_revisited_alt is said to be in lambda-dropped form. Its definition of visit forms a lexical block that is scope-sensitive: it refers to a variable that is declared outside the block.
In contrast, the definition of visit, in Procedure add_revisited, forms a lexical block that is scope-insensitive: all the variables it refers to are either declared locally to the block, or globally. This block can float to the top level, resulting in what is known as two recursive equations:
(define add_revisited_visit (lambda (n1 n2) (if (= n1 0) n2 (+ 1 (add_revisited_visit (- n1 1) n2))))) (define add_revisited_lifted (lambda (n1 n2) (add_revisited_visit n1 n2)))
The result is a Scheme program in lambda-lifted form, that passes the unit test too:
> (unit-tests-for-add add_revisited_lifted) #t >
Program transformations exist that lambda-lift a block-structured, scope-sensitive program into recursive equations, and conversely that lambda-drop recursive equations into a block-structured, scope-sensitive program.
Parity of natural numbers, revisited¶
Let us revisit the two mutually tail-recursive procedures that determine whether a natural number is odd or even. This time, we declare them locally with a letrec-expression:
(define unit-tests-for-one_or_the_other
(lambda (candidate)
(and (equal? (candidate 0)
'(#t #f))
(equal? (candidate 1)
'(#f #t))
(equal? (candidate 8)
'(#t #f))
(equal? (candidate 9)
'(#f #t))
;;;
)))
(define one_or_the_other
(lambda (n)
(letrec ([even? (lambda (n)
(if (= n 0)
#t
(odd? (- n 1))))]
[odd? (lambda (n)
(if (= n 0)
#f
(even? (- n 1))))])
(list (even? n) (odd? n)))))
This procedure passes its unit test:
> (unit-tests-for-one_or_the_other one_or_the_other)
#t
>
Graphically:
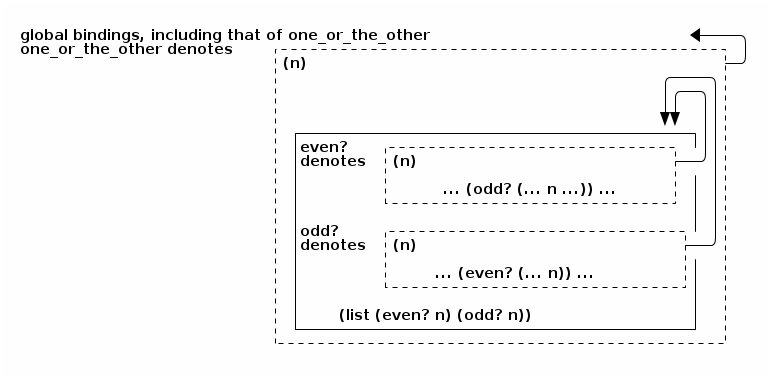
- The expression (list (even? n) (odd? n)), which contains the
initial calls to even? and to odd?, is evaluated in an
environment where
- even? and odd? denote two monadic procedures (the dashed boxes just above) whose lexical scope (the arrows exiting each of the dashed boxes) contains their mutually recursive binding (the arrows are circular and point to the same place, and so even? and odd? can refer to themselves and to each other), and where
- n denotes the actual parameter of the anonymous procedure denoted by one_or_the_other, which is bound in the global environment.
- The expression (odd? (- n 1)), i.e., the recursive call to
odd?, is evaluated in an environment where
- even? and odd? are bound recursively in a mutual way,
- n denotes the actual parameter of the recursive procedure denoted by even?, and where
- - denotes the predefined procedure that subtracts its second argument from its first argument.
- The expression (even? (- n 1)), i.e., the recursive call to
even?, is evaluated in an environment where
- even? and odd? are bound recursively in a mutual way,
- n denotes the actual parameter of the recursive procedure denoted by odd?, and where
- - denotes the predefined procedure that subtracts its second argument from its first argument.
Exercise BB¶
Write a version of one_or_the_other with a letrec-expression that declares only one local recursive procedure that takes two arguments – a natural number and a Boolean:
(define one_or_the_other_alt
(lambda (n)
(letrec ([visit (lambda (n b)
...)])
(list (visit n #t) (visit n #f)))))
Make sure to verify that your procedure passes the unit test:
> (unit-tests-for-one_or_the_other one_or_the_other_alt)
#t
>
Desugaring let-expressions¶
A let-expression such as
(let ([x1 e1] [x2 e2] ... [xN eN]) e0)
is syntactic sugar (a term due to Peter Landin) for
((lambda (x1 x2 ... xN) e0) e1 e2 ... eN)
Here are two consequences:
In this let-expression, each definiens e1, e2, ..., and eN is treated as an actual parameter. Each of them is evaluated, and this evaluation happens in an unspecified order:
> (let ([x (time 10)] [y (time 20)] [z (time 30)]) (list x y z)) (time 20) no collections 0 ms elapsed cpu time 0 ms elapsed real time 0 bytes allocated (time 30) no collections 0 ms elapsed cpu time 0 ms elapsed real time 0 bytes allocated (time 10) no collections 0 ms elapsed cpu time 0 ms elapsed real time 0 bytes allocated (10 20 30) > ((lambda (x y z) (list x y z)) (time 10) (time 20) (time 30)) (time 20) no collections 0 ms elapsed cpu time 0 ms elapsed real time 0 bytes allocated (time 30) no collections 0 ms elapsed cpu time 1 ms elapsed real time 0 bytes allocated (time 10) no collections 0 ms elapsed cpu time 0 ms elapsed real time 0 bytes allocated (10 20 30) >The constraint that all the variables declared in a let-expression must be distinct is really the same constraint that all formal parameters of a lambda-abstraction must be distinct:
> (let ([x 1] [x 2]) x) Exception: invalid parameter list in (lambda (x x) x) Type (debug) to enter the debugger. >
(This error message reveals how Chez Scheme desugars let-expressions into applications of lambda-abstractions.)
Derived special forms: cond¶
In a Scheme program, we typically nest if-expressions in their else branch. Here is an example:
(if 1
10
(if #\a
#\A
(if "hello world"
"HELLO WORLD"
#t)))
Scheme provides syntactic sugar for this type of nested conditional expressions, in the form of cond-expressions. For example, the following cond-expression abbreviates the nested if-expressions above:
(cond
[1
10]
[#\a
#\A]
["hello world"
"HELLO WORLD"]
[else
#t])
The BNF of cond-expressions reads as follows (the non-terminal <cond-clause-binding> is described further down this lecture note):
- <cond-expression> ::= (cond {<cond-clause>}* [else <cond-alternative>])
- <cond-clause> ::= <cond-clause-simple> | <cond-clause-inconsequential> | <cond-clause-binding>
- <cond-clause-simple> ::= [<cond-test> <cond-consequent>]
- <cond-test> ::= <expression>
- <cond-consequent> ::= <expression>
- <cond-alternative> ::= <expression>
- <cond-clause-inconsequential> ::= [<cond-test>]
Note: in most other dialects of Scheme, cond clauses are not delimited with square brackets by default but with ordinary parentheses.
A cond-expression is evaluated as if it were a series of nested if-expressions. The test is evaluated in each successive cond clause:
- if it evaluates to #f, the next clause is considered (and the consequent is not evaluated);
- otherwise, the consequent (if there is one) is evaluated, and its result is the result of the cond-expression.
If all the successive tests have evaluated to #f, the alternative expression is evaluated, and its result is the result of the cond-expression.
An inconsequential cond clause yields the result of the test when it is not #f:
> (cond [1] [else 2])
1
>
Derived special forms: or, revisited¶
- <or-expression> ::= (or {<expression>}*)
The expression
(or e1 e2 ... eN-1 eN)
abbreviates the following conditional expression:
(cond
[e1]
[e2]
...
[eN-1]
[else
eN])
In words: the expressions e1, e2, etc. are evaluated one after each other, until one of them yields another value than #f, in which case this value is the result of the or-expression (and the remaining expressions are not evaluated: they are “short-circuited”), or until the last one, eN, is evaluated; its result is the result of the or-expression.
Note: the above abbreviation of an or-expression with an inconsequential cond-expression is due to Dan Friedman (personal communication, Summer 2011).
Example:
> (or 1 2 3)
1
> (or #f 2 3)
2
> (or #f #f 3)
3
> (or (time #f) (time #f) (time 3) (time 4))
(time #f)
no collections
0 ms elapsed cpu time
0 ms elapsed real time
0 bytes allocated
(time #f)
no collections
0 ms elapsed cpu time
0 ms elapsed real time
0 bytes allocated
(time 3)
no collections
0 ms elapsed cpu time
0 ms elapsed real time
0 bytes allocated
3
>
Derived special forms: cond, revisited¶
- <cond-clause-binding> ::= [<cond-test> => <expression>]
Because in Scheme, everything which is not #f is considered as true, tested values may be more meaningful than #t. To “recover” such tested values, clauses in cond-expressions may be binding: they can be specified with a procedure to apply to the result of the test. So for example, since 10 is not #f, evaluating
(cond [10 => (lambda (x) x)] [else "What was that?"])
becomes equivalent to evaluating
((lambda (x) x) 10)
which yields 10. In the following scenario, the binding clause contains a traced lambda-abstraction, for visualization:
> (cond [10 => (trace-lambda hello (x) x)] [else "What was that?"])
|(hello 10)
|10
10
>
Question: what would be the result of evaluating the following expressions, do you think?
- (cond [(list 10 20) => car] [else "What was that?"])
- (cond [(list 10) => list] [else "What was that?"])
- (cond [(list) => list] [else "What was that?"])
- (cond [(cdr (cons #t #f)) => list] [else "What was that?"])
Derived special forms: or, re2visited¶
The expression
(or e1 e2 ... eN-1 eN)
abbreviates the following conditional expression:
(cond
[e1
=> (lambda (v1) v1)]
[e2
=> (lambda (v2) v2)]
...
[eN-1
=> (lambda (vN-1) vN-1)]
[else
eN])
Or again, because local names do not matter:
(cond
[e1
=> (lambda (v) v)]
[e2
=> (lambda (v) v)]
...
[eN-1
=> (lambda (v) v)]
[else
eN])
Derived special forms: or, re3visited¶
The expression
(or e1 e2 ... eN-1 eN)
also abbreviates the following let-expression:
(let ([x1 e1])
(if x1
x1
(let ([x2 e2])
(if x2
x2
... (let ([xN-1 eN-1])
(if xN-1
xN-1
eN))...))))
where the variables x1, x2, ..., xN-1 are otherwise unused.
Derived special form: case¶
For linguistic comfort, Scheme offers the special form
(case e
[(v1_1 ... vM1_N1)
e1]
[(v2_1 ... vM2_N2)
e2]
...
[(vK_1 ... vMK_NK)
eK]
[else
e0])
to stand for
(let ([v e])
(cond
[(memq v '(v1_1 ... vM1_N1))
e1]
[(memq v '(v2_1 ... vM2_N2))
e2]
...
[(memq v '(vK_1 ... vMK_NK))
eK]
[else
e0]))
where v is a “fresh” variable, i.e., one that does not occur in e1, e2, ..., eK, and e0, and where each case-clause has been mapped into a call to memq. (Procedure memq is predefined, takes two arguments – a value and a list of values – and tests whether the value occurs in the list of values.)
In other words, the two following procedures are equivalent:
(define 246?
(lambda (x)
(if (memq x '(2 4 6))
#t
#f)))
(define 246?_alt
(lambda (x)
(case x
[(2 4 6)
#t]
[else
#f])))
Resources¶
- The Scheme code for the present lecture note (latest version: 11 Sep 2025).
Version¶
Created [11 Sep 2025]