Language processors for Boolean expressions¶
Goal¶
Let us successively describe how to implement
- a BNF of Boolean expressions,
- a syntax checker (i.e., a procedure that checks whether a given value conforms to this BNF),
- an interpreter (i.e., a procedure that evaluates a given Boolean expression in a given environment),
- a BNF of Boolean expressions in negational normal form,
- a syntax checker, an interpreter, and an embedding for this BNF, and
- a negational normalizer (i.e., a procedure that transforms a Boolean expression into a Boolean expression in negational normal form).
BNF of Boolean expressions¶
A Boolean expression is either a variable, a conjunction, a disjunction, or a negation.
- <boolean-expression> ::= (var <name>) | (conj <boolean-expression> <boolean-expression>) | (disj <boolean-expression> <boolean-expression>) | (neg <boolean-expression>)
- <name> ::= ...any Scheme symbol...
To implement this BNF, we need constructors, predicates, and accessors.
Each constructor simply constructs a tagged list:
(define make-var (lambda (x) (list 'var x))) (define make-conj (lambda (f1 f2) (list 'conj f1 f2))) (define make-disj (lambda (f1 f2) (list 'disj f1 f2))) (define make-neg (lambda (f) (list 'neg f)))
We are now in position to construct Boolean expressions, either with these constructors... or without:
(define be0 (make-conj (make-disj (make-var 'x) (make-neg (make-var 'y))) (make-neg (make-conj (make-var 'z) (make-var 'x))))) (define be0-alt '(conj (disj (var x) (neg (var y))) (neg (conj (var z) (var x))))) (define be1 (make-disj (make-var 'x) (make-neg (make-var 'x)))) (define be1-alt '(disj (var x) (neg (var x))))
To make sure, let us test whether the canonically constructed abstract-syntax trees are equal to the quoted ones:
> (equal? be0 be0-alt) #t > (equal? be1 be1-alt) #t >
Here is the corresponding positive unit-test procedure:
(define test-check-boolean-expression (lambda (candidate) (and (candidate be0) (candidate be1) ;;; add more tests here )))
Given a procedure implementing a syntax checker, this testing procedure successively applies it to each of the two well-formed Boolean expressions to verify that they syntax-check.
Each predicate simply verifies whether its argument is a tagged proper list of the appropriate length, using a suitable auxiliary procedure, proper-list-of-given-length?:
(define proper-list-of-given-length? (lambda (v n) (or (and (null? v) (= n 0)) (and (pair? v) (> n 0) (proper-list-of-given-length? (cdr v) (- n 1)))))) (define is-var? (lambda (v) (and (pair? v) (equal? (car v) 'var) (proper-list-of-given-length? (cdr v) 1)))) (define is-conj? (lambda (v) (and (pair? v) (equal? (car v) 'conj) (proper-list-of-given-length? (cdr v) 2)))) (define is-disj? (lambda (v) (and (pair? v) (equal? (car v) 'disj) (proper-list-of-given-length? (cdr v) 2)))) (define is-neg? (lambda (v) (and (pair? v) (equal? (car v) 'neg) (proper-list-of-given-length? (cdr v) 1))))
Each accessor assumes a well-formed input and simply picks the corresponding sub-expression:
(define var-1 (lambda (v) (list-ref v 1))) (define conj-1 (lambda (v) (list-ref v 1))) (define conj-2 (lambda (v) (list-ref v 2))) (define disj-1 (lambda (v) (list-ref v 1))) (define disj-2 (lambda (v) (list-ref v 2))) (define neg-1 (lambda (v) (list-ref v 1)))
A syntax checker for Boolean expressions¶
We are now in position to write a syntax checker to decide whether a given value is a well-formed Boolean expression. The syntax checker attempts to traverse its input recursively as per the inductive definition of Boolean expressions (i.e., the BNF). If it cannot, the input is not syntactically correct:
(define check-boolean-expression
(lambda (v)
(cond
[(is-var? v)
(symbol? (var-1 v))]
[(is-conj? v)
(and (check-boolean-expression (conj-1 v))
(check-boolean-expression (conj-2 v)))]
[(is-disj? v)
(and (check-boolean-expression (disj-1 v))
(check-boolean-expression (disj-2 v)))]
[(is-neg? v)
(check-boolean-expression (neg-1 v))]
[else
#f])))
Let us test this syntax checker:
> (test-check-boolean-expression check-boolean-expression)
#t
>
Success.
Exercise 02¶
Implement an unparser from the abstract syntax of Boolean expressions (i.e., the syntax specified by the BNF) to the concrete syntax of Scheme:
- <expression> ::= <variable> | (and <expression> <expression>) | (or <expression> <expression>) | (not <expression>)
(define test-unparser (lambda (candidate) (and (equal? (candidate (make-variable 'x)) 'x) (equal? (candidate (make-negation (make-variable 'x))) '(not x)) ;;; etc. )))
Implement a parser from the concrete syntax of Scheme to the abstract syntax of Boolean expressions.
(define test-parser (lambda (candidate) (and (equal? (candidate 'x) (make-variable 'x)) (equal? (candidate '(not x)) (make-negation (make-variable 'x))) ;;; etc. )))
Are your parser and unparser inverses of each other?
An interpreter for Boolean expressions¶
To evaluate a well-formed Boolean expression in a given Environments, conceptually, we recursively traverse it. In the base case of symbols, we look them up in the given environment, which is represented here as an association list (see Environments as association lists). Otherwise, we interpret conjunction with and, disjunction with or, and negation with not:
(define evaluate-boolean-expression
(lambda (expression environment)
(letrec ([process (lambda (e)
(cond
[(is-var? e)
(alist-lookup (var-1 e)
environment
(lambda (v)
v)
(lambda (x)
(errorf 'evaluate-boolean-expression
"unbound name: ~s"
x)))]
[(is-conj? e)
(let ([v1 (process (conj-1 e))]
[v2 (process (conj-2 e))])
(and v1 v2))]
[(is-disj? e)
(let ([v1 (process (disj-1 e))]
[v2 (process (disj-2 e))])
(or v1 v2))]
[(is-neg? e)
(let ([v (process (neg-1 e))])
(not v))]
[else
(errorf 'evaluate-boolean-expression
"illegal sub-expression: ~s"
e)]))])
(process expression))))
(Note how each recursive call to process matches the inductive definition of Boolean expressions and how each call is over the result of an accessor: process is structurally recursive.)
We can now verify that evaluating (disj x (neg x)) yields #t, whether x denotes #t or #f:
> (evaluate-boolean-expression be1 (alist-extend 'x #t alist-mt))
#t
> (evaluate-boolean-expression be1 (alist-extend 'x #f alist-mt))
#t
>
Food for thought:
Do you think this interpreter evaluates conjunctions from left to right? If not, adjust it to make it so.
Because false is absorbing for conjunction, the interpreter could implement “short-cut evaluation” by only evaluating the second component of a conjunction if evaluating the first component does not yield false.
Copy the definition of evaluate-boolean-expression and rename it to evaluate-boolean-expression_short-cut. (This will require three changes: in the name of the definition and in the two error messages.)
How would you modify the definition of evaluate-boolean-expression_short-cut so that it performs short-cut evaluation for conjunctions? (Hint: use an if-expression instead of a let-expression.)
Rather than an if-expression, could you use an and-expression to make the interpreter perform short-cut evaluation for conjunctions?
Consider the syntactically incorrect Boolean expression (conj (var x) "hello world"), and evaluate it in an environment where x denotes false, first with your modified interpreter and then with the original interpreter:
> (evaluate-boolean-expression_short-cut '(conj (var x) "hello world") (alist-extend 'x #f alist-mt)) ... > (evaluate-boolean-expression '(conj (var x) "hello world") (alist-extend 'x #f alist-mt)) ... >Are the results the same? What do you conclude?
More food for thought:
- Do you think the interpreter (whether the original one or the one you modified) evaluates disjunctions from left to right? If not, adjust your modified interpreter so that it does so.
- Modify your modified interpreter further so that it implements short-cut evaluation for disjunctions.
De Morgan’s laws¶
Boolean expressions can be inter-converted using De Morgan’s laws as well as by removing or adding two consecutive negations:
(neg (conj e1 e2)) <=> (disj (neg e1) (neg e2))
(neg (disj e1 e2)) <=> (conj (neg e1) (neg e2))
(neg (neg e)) <=> e
The equivalence sign <=> means that converting any sub-part of a Boolean expression preserves the meaning of this Boolean expression. More concretely, given a Boolean expression e1, we can convert any part of it, even repeatedly, until we obtain some Boolean expression e2. For any given environment, evaluating e1 and e2 in this environment will yield the same result.
BNF of Boolean expressions in negational normal form¶
In a Boolean expression in negational normal form, only names are negated:
- <boolean-expression_nnf> ::= (posvar <name>) | (negvar <name>) | (conj_nnf <boolean-expression_nnf> <boolean-expression_nnf>) | (disj_nnf <boolean-expression_nnf> <boolean-expression_nnf>)
- <name> ::= ...any Scheme symbol...
Exercise 03¶
The primary goal of this exercise is to implement the BNF of Boolean expressions in negational normal form. Its secondary goal is to see whether you have the reflex of setting up unit tests as you go:
Implement the BNF of negational normal forms.
To this end, you will need to define constructors (make-var_nnf, make-conj_nnf, make-disj_nnf, and make-negv_nnf), predicates (is-var_nnf?, is-conj_nnf?, is-disj_nnf?, and is-neg_nnf?), and accessors (var_nnf-1, conj_nnf-1, conj_nnf-2, disj_nnf-1, disj_nnf-2, and neg_nnf-1).
(Ahem, also remember to create a sample of well-formed Boolean expressions in negational normal form, and a sample of ill-formed ones.)
Implement a syntax checker for Boolean expressions in negational normal form, i.e., a unary procedure check-boolean-expression_nnf that tests whether its argument is a well-formed Boolean expression in negational normal form.
(If you had the idea of setting up a positive unit test and a negative unit test for your syntax checker, that would be wonderful.)
Boolean expressions in negational normal form are a sublanguage of Boolean expressions. Implement a procedure that embeds a Boolean expression in negational normal form into a Boolean expression. Your procedure should be structurally recursive, i.e., the argument of each recursive call should be an accessor.
Solution:
(define embed-boolean-expression_nnf-into-boolean-expression (lambda (v) (cond [(is-var_nnf? v) (make-var (var_nnf-1 v))] [(is-conj_nnf? v) (make-conj (embed-boolean-expression_nnf-into-boolean-expression (conj_nnf-1 v)) (embed-boolean-expression_nnf-into-boolean-expression (conj_nnf-2 v)))] [(is-disj_nnf? v) (make-disj (embed-boolean-expression_nnf-into-boolean-expression (disj_nnf-1 v)) (embed-boolean-expression_nnf-into-boolean-expression (disj_nnf-2 v)))] [(is-neg_nnf? v) (make-neg (make-var (neg_nnf-1 v)))] [else (errorf 'embed-boolean-expression_nnf-into-boolean-expression "not a Boolean expression in negational normal form: ~s" v)])))
(It would be fantastic if you had the idea of using the Boolean expressions in negational normal form from your unit test to set up a new unit test that verifies that the result of embed-boolean-expression_nnf-into-boolean-expression satisfies the syntax checker for Boolean expressions.)
Define a procedure evaluate-boolean-expression_nnf that implements an interpreter for Boolean expressions in negational normal form.
(Hey, how about setting up a unit test for your interpreter?)
Define a procedure normalize-boolean-expression that normalizes a well-formed Boolean expression into a well-formed Boolean expression in negational normal form, and test it with the predicate you implemented in Part b of the present exercise. Your procedure should operate in one recursive descent over the input Boolean expression. It should be structurally recursive, i.e., the argument of each recursive call should be an accessor.
Verify on a handful of examples (or even better in a unit test, yay) that for any given environment, evaluating a Boolean expression and evaluating the corresponding negational normal form yield the same result.
To this end, here is a testing procedure:
(define normalize-boolean-expression (lambda (e) (errorf 'normalize-boolean-expression "not implemented yet"))) (define evaluate-boolean-expression_nnf (lambda (expression environment) (errorf 'evaluate-boolean-expression_nnf "not implemented yet"))) (define test-the-normalizer (lambda (expression environment) (boolean=? (evaluate-boolean-expression expression environment) (evaluate-boolean-expression_nnf (normalize-boolean-expression expression) environment))))
This whole exercise is diagrammatically summarized as follows:
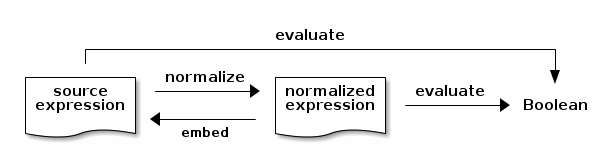
One can formally prove that the normalization procedure is a left inverse of the embedding procedure: embedding a normal form into a source expression and normalizing the result yields this normal form back. This proof is carried out by structural induction over the syntax of normal forms. (Hence the importance of defining the normalizer in a structurally recursive way: otherwise we could not apply the induction hypotheses.)
In case the previous paragraph comes across as more confusing than informative, take a closer look at the diagram just above. See the two converse arrows between source expressions and normalized expressions?
Normalizing an expression and then embedding the resulting normal form back into an expression does not give back the same syntactic expression, in general, unless the expression only negated names to start with. Diagrammatically:
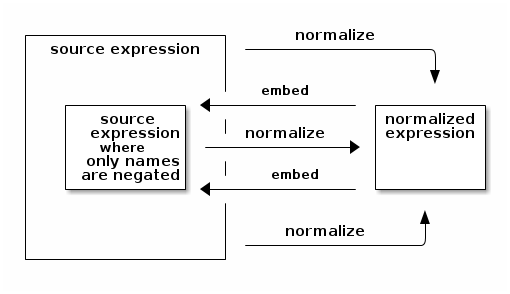
However, embedding a normal form and then normalizing the result gives back the same syntactic normal form, always. Here is a testing procedure to this end:
(define test-the-embedding (lambda (expression) (let ([expression_nnf (normalize-boolean-expression expression)]) (equal? (normalize-boolean-expression (embed-boolean-expression_nnf-into-boolean-expression expression_nnf)) expression_nnf))))
(Boy, would this procedure come handy if anyone were to set up a unit test right about here.)
Besides, evaluating the expression and evaluating its normal form give the same semantic result, always – that was the point of Part f of the present exercise.
On the idempotence of negational normalization¶
Let us define negational normalization as a source-to-source program transformation by composing embed-boolean-expression_nnf-into-boolean-expression and normalize-boolean-expression:
(define normalize-boolean-expression_source-to-source
(lambda (expression)
(embed-boolean-expression_nnf-into-boolean-expression
(normalize-boolean-expression
expression))))
This source-to-source negational normalization is idempotent in that applying it to its output yields the same output.
Here is the corresponding unit test:
(define test-idempotence-of-normalize-boolean-expression_source-to-source
(lambda ()
(and (let ([be0_normalized (normalize-boolean-expression_source-to-source be0)])
(equal? (normalize-boolean-expression_source-to-source be0_normalized)
be0_normalized))
(let ([be1_normalized (normalize-boolean-expression_source-to-source be1)])
(equal? (normalize-boolean-expression_source-to-source be1_normalized)
be1_normalized))
;;; add more tests here
)))
Checkpoint¶
We have used Scheme to study a variety of programming-language artifacts relative to Boolean expressions: two BNFs, two syntax checkers, two interpreters, a normalizer, and its left inverse.
Version¶
Created [09 Oct 2025]