Mini-project about three language processors for arithmetic expressions¶
The goal of this mini-project is to implement an interpreter, a compiler, and a virtual machine for arithmetic expressions.
The source language¶
The source language is that of arithmetic expressions for integers with addition, subtraction, quotient, and remainder:
n ::= ...any integer...
e ::= n | e + e | e - e | e quo e | e rem e
Source abstract syntax¶
The abstract syntax of the source language is implemented with the following OCaml data types:
type arithmetic_expression =
| Literal of int
| Plus of arithmetic_expression * arithmetic_expression
| Minus of arithmetic_expression * arithmetic_expression
| Quotient of arithmetic_expression * arithmetic_expression
| Remainder of arithmetic_expression * arithmetic_expression;;
type source_program =
| Source_program of arithmetic_expression;;
So for example, the expression (100 + (10 + 1)) / 2 is represented as follows:
Source_program (Quotient (Plus (Literal 100, Plus (Literal 10, Literal 1)), Literal 2))
The overarching goal¶
The overarching goal of this mini-project is to implement an interpreter for the language of arithmetic expressions, a compiler from the language of arithmetic expressions to byte code, and a virtual machine for byte code in a way such that interpreting an arithmetic expression should yield the same result as compiling this arithmetic expression and running the resulting compiled program – be it an integer or an error message:
type expressible_value =
| Expressible_int of int
| Expressible_msg of string;;
Pictorially, the following diagram should commute:
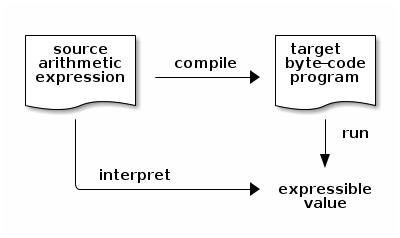
A source interpreter for arithmetic expressions¶
As per the definition of expressible_value, interpreting an arithmetic expression should yield either an integer or an error message.
Intuitively, the unit-test function is simple to write:
- any arithmetic expression with a quotient or a remainder where the second argument is 0 should be mapped to an error since no integer can be divided by 0;
- all other arithmetic expressions should be mapped to the integer representing the result of evaluating the arithmetic expression.
For example:
let int_test_interpret candidate_interpret =
(* int_test_interpret : (source_program -> expressible_value) -> bool *)
let b0 = (candidate_interpret (Source_program (Literal 0))
= Expressible_int 0)
and b1 = (candidate_interpret (Source_program (Plus (Literal 1, Literal 0)))
= Expressible_int 1)
and b2 = (candidate_interpret (Source_program (Plus (Literal 10, Plus (Literal 1, Literal 0))))
= Expressible_int 11)
and b3 = (candidate_interpret (Source_program (Plus (Plus (Literal 10, Literal 1), Literal 0)))
= Expressible_int 11)
and b4 = (candidate_interpret (Source_program (Minus (Literal 10, Literal 10)))
= Expressible_int 0)
(* etc. *)
in b0 && b1 && b2 && b3 && b4;;
let msg_test_interpret candidate_interpret =
(* msg_test_interpret : (source_program -> expressible_value) -> bool *)
let b0 = (candidate_interpret (Source_program (Quotient (Literal 0, Literal 0)))
= Expressible_msg "quotient of 0 over 0")
and b1 = (candidate_interpret (Source_program (Remainder (Literal 0, Literal 0)))
= Expressible_msg "remainder of 0 over 0")
(* etc. *)
in b0 && b1;;
(Obviously, these unit tests should be fleshed out.)
Interpreting a source program (Source_program e) consists in evaluating e, and formally, this evaluation is specified inductively, following the structure of arithmetic expressions:
base case:
for any integer n (noting its syntactic representation as n),
evaluating Literal n yields the integer n
induction step for additions:
for any arithmetic expression e1 that was evaluated as the expressible value ev1 (which is the first induction hypothesis) and any arithmetic expression e2 that was evaluated as the expressible value ev2 (which is the second induction hypothesis),
if ev1 is the integer n1 and
if ev2 is the integer n2,
then evaluating Plus (e1, e2) yields the integer obtained by adding n1 and n2
if ev2 is the error message s
then evaluating Plus (e1, e2) yields s
if ev1 is the error message s
then evaluating Plus (e1, e2) yields s
induction step for subtractions:
for any arithmetic expression e1 that was evaluated as the expressible value ev1 (which is the first induction hypothesis) and any arithmetic expression e2 that was evaluated as the expressible value ev2 (which is the second induction hypothesis),
if ev1 is the integer n1 and
if ev2 is the integer n2,
then evaluating Minus (e1, e2) yields the integer obtained by subtracting n2 from n1
if ev2 is the error message s
then evaluating Minus (e1, e2) yields s
if ev1 is the error message s
then evaluating Minus (e1, e2) yields s
induction step for quotients:
for any arithmetic expression e1 that was evaluated as the expressible value ev1 (which is the first induction hypothesis) and any arithmetic expression e2 that was evaluated as the expressible value ev2 (which is the second induction hypothesis),
if ev1 is the integer n1 and
if ev2 is the integer n2,
if n2 is 0
then evaluating Quotient (e1, e2) yields the error message “quotient of n1 over 0”
if n2 is not 0
then evaluating Quotient (e1, e2) yields the quotient of n1 over n2
if ev2 is the error message s
then evaluating Quotient (e1, e2) yields s
if ev1 is the error message s
then evaluating Quotient (e1, e2) yields s
induction step for remainders:
for any arithmetic expression e1 that was evaluated as the expressible value ev1 (which is the first induction hypothesis) and any arithmetic expression e2 that was evaluated as the expressible value ev2 (which is the second induction hypothesis),
if ev1 is the integer n1 and
if ev2 is the integer n2,
if n2 is 0
then evaluating Remainder (e1, e2) yields the error message “remainder of n1 over 0”
if n2 is not 0
then evaluating Remainder (e1, e2) yields the remainder of n1 over n2
if ev2 is the error message s
then evaluating Remainder (e1, e2) yields s
if ev1 is the error message s
then evaluating Remainder (e1, e2) yields s
Task 1¶
Implement an interpreter for the source language as an OCaml function that satisfies the specification above:
let interpret (Source_program e) =
(* interpret : source_program -> expressible_value *)
let rec evaluate e =
(* evaluate : arithmetic_expression -> expressible_value *)
...
in evaluate e;;
This source interpreter should pass the unit tests.
Subsidiary questions:
- Does your interpreter evaluate from left to right or from right to left?
- Does it make any observable difference whether your interpreter evaluates from left to right or from right to left?
The target language¶
The target language is that of byte-code programs:
n ::= ...any integer...
bci ::= push n | add | sub | quo | rem
p ::= {bci}*
Byte-code instructions¶
The byte-code instructions in the target language are implemented with the following OCaml data type:
type byte_code_instruction =
| Push of int
| Add
| Sub
| Quo
| Rem;;
Target abstract syntax¶
The abstract syntax of the target language is implemented with the following OCaml data type of byte-code programs:
type target_program =
| Target_program of byte_code_instruction list;;
A processor for byte-code instructions¶
Each byte-code instruction is to be executed in a virtual machine (i.e., an interpreter for byte-code programs) that threads a data stack, represented here as a list of integers:
type stackable_value = int;;
type data_stack = stackable_value list;;
type result_of_decoding_and_execution =
| OK of data_stack
| KO of string;;
Intuitively, Push n is processed by pushing n on the current data stack and returning the resulting stack, and all the other byte-code instructions are processed by
- popping two integers (so there must be at least two integers on top of the stack, otherwise it is an error), and
- performing the associated operation:
- if this is an error case (e.g., a division by 0 is attempted), then an error message should be returned
- if this is not an error case, then the operation should be performed, its result should be pushed on the current data stack, and the resulting stack should be returned.
The following unit-test function illustrates salient cases:
let test_decode_execute candidate_decode_execute =
(* test_decode_execute : (byte_code_instruction -> data_stack -> result_of_decoding_and_execution) -> bool *)
let b0 = (candidate_decode_execute (Push 33) []
= OK [33])
and b1 = (candidate_decode_execute (Push 33) [34; 35]
= OK [33; 34; 35])
and b2 = (candidate_decode_execute Add []
= KO "stack underflow for Add")
and b3 = (candidate_decode_execute Add [10]
= KO "stack underflow for Add")
and b4 = (candidate_decode_execute Add [10; 10]
= OK [20])
and b5 = (candidate_decode_execute Quo [0; 0]
= KO "quotient of 0 over 0")
(* etc. *)
in b0 && b1 && b2 && b3 && b4 && b5;;
Formally, the function is specified by cases, following the structure of byte-code instructions:
Push n, where n represents the integer n:
for any data stack ds (represented as ds), processing the byte-code instruction Push n consists in pushing n on top of ds and returning the resulting stack, i.e., n :: ds
Add
if the data stack is empty, processing the byte-code instruction Add with this data stack yields the error message "stack underflow for Add"
if the data stack only contains one integer, processing the byte-code instruction Add with this data stack yields the error message "stack underflow for Add"
if the data stack contains at least two integers on top of the rest of the data stack, these two integers represent the two arguments of the addition operation we are about to perform
processing the byte-code instruction Add with this data stack consists in popping the two integers off the data stack; let n1 be the integer that stands for the first argument of the addition operation and let n2 be the integer that stands for the second argument of the addition operation:
processing Add consists in adding n1 and n2, pushing the resulting integer (represented as n3) on the popped data stack (represented as ds''), and returning this pushed data stack (i.e., n3 :: ds'')
Sub
if the data stack is empty, processing the byte-code instruction Sub with this data stack yields the error message "stack underflow for Sub"
if the data stack only contains one integer, processing the byte-code instruction Sub with this data stack yields the error message "stack underflow for Sub"
if the data stack contains at least two integers on top of the rest of the data stack, these two integers represent the two arguments of the subtraction operation we are about to perform
processing the byte-code instruction Sub with this data stack consists in popping the two integers off the data stack; let n1 be the integer that stands for the first argument of the subtraction operation and let n2 be the integer that stands for the second argument of the subtraction operation:
processing Sub consists in subtracting n2 from n1, pushing the resulting integer (represented as n3) on the popped data stack (represented as ds''), and returning this pushed data stack (i.e., n3 :: ds'')
Quo
if the data stack is empty, processing the byte-code instruction Quo with this data stack yields the error message "stack underflow for Quo"
if the data stack only contains one integer, processing the byte-code instruction Quo with this data stack yields the error message "stack underflow for Quo"
if the data stack contains at least two integers on top of the rest of the data stack, these two integers represent the two arguments of the quotient operation we are about to perform
processing the byte-code instruction Quo with this data stack consists in popping the two integers off the data stack; let n1 be the integer that stands for the first argument of the quotient operation (represented as n1) and let n2 be the integer that stands for the second argument of the quotient operation:
if n2 is 0
then processing Quo yields the error message "quotient of n1 over 0"
if n2 is not 0
then processing Quo consists in computing the quotient of n1 over n2, pushing the resulting integer (represented as n3) on the popped data stack (represented as ds''), and returning this pushed data stack (i.e., n3 :: ds'')
Rem
if the data stack is empty, processing the byte-code instruction Rem with this data stack yields the error message "stack underflow for Rem"
if the data stack only contains one integer, processing the byte-code instruction Rem with this data stack yields the error message "stack underflow for Rem"
if the data stack contains at least two integers on top of the rest of the data stack, these two integers represent the two arguments of the remainder operation we are about to perform
processing the byte-code instruction Rem with this data stack consists in popping the two integers off the data stack; let n1 be the integer that stands for the first argument of the remainder operation (represented as n1) and let n2 be the integer that stands for the second argument of the remainder operation:
if n2 is 0
then processing Rem yields the error message "remainder of n1 over 0"
if n2 is not 0
then processing Rem consists in computing the remainder of n1 over n2, pushing the resulting integer (represented as n3) on the popped data stack (represented as ds''), and returning this pushed data stack (i.e., n3 :: ds'')
Task 2¶
Implement a processor for one byte-code instruction as an OCaml function that satisfies the specification just above:
let decode_execute bci ds =
(* decode_execute : byte_code_instruction -> data_stack -> result_of_execution *)
...;;
The processor should pass the unit tests.
A virtual machine for byte-code programs¶
Interpreting a byte-code program yields a final result, i.e., an integer or an error message, just like interpreting an arithmetic expression.
Intuitively, the unit-test function is simple to write:
- any byte-code program involving a quotient or a remainder where the second argument is 0 should be mapped into an error since no integer can be divided by 0;
- any byte-code program whose execution triggers a stack underflow should be mapped to an error;
- any byte-code program whose execution yields an empty stack should be mapped to an error;
- any byte-code program whose execution yields a stack containing one integer should be mapped to this integer;
- any byte-code program whose execution yields a stack containing more than one integer should be mapped to an error.
For example:
let int_test_run candidate_run =
(* int_test_run : target_program -> expressible_value *)
let b0 = (candidate_run (Target_program [Push 0])
= Expressible_int 0)
and b1 = (candidate_run (Target_program [Push 1; Push 0; Add])
= Expressible_int 1)
and b2 = (candidate_run (Target_program [Push 10; Push 1; Push 0; Add; Add])
= Expressible_int 11)
and b3 = (candidate_run (Target_program [Push 10; Push 1; Add; Push 0; Add])
= Expressible_int 11)
and b4 = (candidate_run (Target_program [Push 10; Push 10; Sub])
= Expressible_int 0)
(* etc. *)
in b0 && b1 && b2 && b3 && b4;;
let msg_test_run candidate_run =
(* msg_test_run : target_program -> expressible_value *)
let b0 = (candidate_run (Target_program [])
= Expressible_msg "stack underflow at the end")
and b1 = (candidate_run (Target_program [Push 2; Push 3])
= Expressible_msg "stack overflow at the end")
and b2 = (candidate_run (Target_program [Add])
= Expressible_msg "stack underflow for Add")
and b3 = (candidate_run (Target_program [Push 2; Add])
= Expressible_msg "stack underflow for Add")
and b4 = (candidate_run (Target_program [Push 0; Push 0; Quo])
= Expressible_msg "quotient of 0 over 0")
and b5 = (candidate_run (Target_program [Push 0; Push 0; Rem])
= Expressible_msg "remainder of 0 over 0")
(* etc. *)
in b0 && b1 && b2 && b3 && b4 && b5;;
(Obviously, these unit tests should be fleshed out.)
Formally, the target interpreter is specified by following the structure of byte-code programs. It uses an auxiliary fetch-decode-execute function that follows the inductive structure of lists of byte-code instructions.
A sample of executions¶
The virtual machine has two components, a program pointer and a data stack. It executes each byte-code instruction in the byte-code program, one after another.
Here are some simple examples of runs:
Consider the following byte-code program:
Target_program [Push 32]
- The machine starts with [Push 32] and with an empty data stack, [].
- Processing the byte-code instruction Push 32 has the effect of pushing 32 on the data stack, yielding [32], and the machine continues with the rest of the list of byte-code instructions, i.e., [].
- Since the list of byte-code instructions is empty, and since there is one integer in the data stack, the machine stops with this integer, and the result is 32.
Consider the following byte-code program:
Target_program [Push 10; Push 10; Add]
- The machine starts with [Push 10; Push 10; Add] and with an empty data stack, [].
- Processing the byte-code instruction Push 10 has the effect of pushing 10 on the data stack, yielding [10], and the machine continues with the rest of the list of byte-code instructions, i.e., [Push 10; Add].
- Processing the byte-code instruction Push 10 has the effect of pushing 10 on the data stack, yielding [10; 10], and the machine continues with the rest of the list of byte-code instructions, i.e., [Add].
- Processing the byte-code instruction Add has the effect of popping the two integers from the data stack, adding them, and pushing the resulting integer on the data stack, yielding [20], and the machine continues with the rest of the list of byte-code instructions, i.e., [].
- Since the list of byte-code instructions is empty, and since there is one integer in the data stack, the machine stops with this integer, and the result is 20.
Consider the following byte-code program:
Target_program [Push 10; Push 20]
- The machine starts with [Push 10; Push 20] and with an empty data stack, [].
- Processing the byte-code instruction Push 10 has the effect of pushing 10 on the data stack, yielding [10], and the machine continues with the rest of the list of byte-code instructions, i.e., [Push 20].
- Processing the byte-code instruction Push 20 has the effect of pushing 20 on the data stack, yielding [20; 10], and the machine continues with the rest of the list of byte-code instructions, i.e., [].
- Since the list of byte-code instructions is empty, and since there is more than one integer in the data stack, the machine stops with the error message "stack overflow at the end".
Task 3¶
Implement an interpreter for the target language (i.e., a virtual machine) as an OCaml function that satisfies the specification just above.
This target interpreter should pass the unit tests.
Solution for Task 3¶
The interpreter uses a fetch-decode-execute loop until it runs out of byte-code instructions and yields a result that is mapped to an expressible value:
let run (Target_program bcis) =
(* run : target_program -> expressible_value *)
let rec fetch_decode_execute bcis ds =
(* fetch_decode_execute : byte_code_instruction list -> data_stack -> result_of_execution *)
match bcis with
| [] ->
OK ds
| bci :: bcis' ->
(match decode_execute bci ds with
| OK ds' ->
fetch_decode_execute bcis' ds'
| KO s ->
KO s)
in match fetch_decode_execute bcis [] with
| OK [] ->
Expressible_msg "stack underflow at the end"
| OK (n :: []) ->
Expressible_int n
| OK (n :: _ :: _) ->
Expressible_msg "stack overflow at the end"
| KO s ->
Expressible_msg s;;
The fetch-decode-execute loop starts with an empty data stack, and it is expected to end either with a data stack containing one element – the resulting value, or with an error message – the resulting error message.
Food for thought:
The resource file for the present lecture note contains a traced version of run that makes it possible to visualize the fetch-decode-execute loop in action:
# traced_run (Target_program [Push 16; Push 16; Add]);; fetch_decode_execute [Push 16; Push 16; Add] [] fetch_decode_execute [Push 16; Add] [16] fetch_decode_execute [Add] [16; 16] fetch_decode_execute [] [32] fetch_decode_execute <- OK [32] - : expressible_value = Expressible_int 32 # traced_run (Target_program [Push 0; Push 0; Quo; Push 16; Add]);; fetch_decode_execute [Push 0; Push 0; Quo; Push 16; Add] [] fetch_decode_execute [Push 0; Quo; Push 16; Add] [0] fetch_decode_execute [Quo; Push 16; Add] [0; 0] fetch_decode_execute <- KO "quotient of 0 over 0" - : expressible_value = Expressible_msg "quotient of 0 over 0" #
Analysis:
- At each iteration of the fetch-decode-execute loop, the current program and the current data stack are printed out.
- In the second interaction, the virtual machine stops with an error message.
A compiler from arithmetic expressions to byte-code programs¶
The compiler translates source programs to target programs.
Intuitively, it is a “postfix compiler” that first translates the two arguments of any binary operation and then emits a byte-code instruction that corresponds to the operation: Add for Plus, Sub for Minus, etc.
For example:
let test_compile candidate_compile =
(* test_compile : (source_program -> byte_code_program) -> bool *)
let b0 = (candidate_compile (Source_program (Literal 32))
= Target_program [Push 32])
and b1 = (candidate_compile (Source_program (Plus (Literal 1, Literal 10)))
= Target_program [Push 1; Push 10; Add])
and b2 = (candidate_compile (Source_program (Plus (Plus (Literal 1, Literal 10), Plus (Literal 20, Literal 2))))
= Target_program [Push 1; Push 10; Add; Push 20; Push 2; Add; Add])
and b3 = (candidate_compile (Source_program (Plus (Literal 1, Plus (Literal 10, Plus (Literal 20, Literal 2)))))
= Target_program [Push 1; Push 10; Push 20; Push 2; Add; Add; Add])
and b4 = (candidate_compile (Source_program (Plus (Literal 1, Plus (Plus (Literal 10, Literal 20), Literal 2))))
= Target_program [Push 1; Push 10; Push 20; Add; Push 2; Add; Add])
and b5 = (candidate_compile (Source_program (Quotient (Literal 4, Literal 5)))
= Target_program [Push 4; Push 5; Quo])
(* etc. *)
in b0 && b1 && b2 && b3 && b4 && b5;;
(Obviously, this unit-test function should be fleshed out.)
Compiling a source program (Source_program e) consists in translating e, and formally, this translation is specified inductively, following the structure of arithmetic expressions to construct a list of byte-code instructions:
base case:
for any integer n (noting its syntactic representation as n),
translating Literal n yields the singleton list containing the byte-code instruction Push n
induction step for additions:
for any arithmetic expression e1 (represented as e1) that was translated as the list of byte-code instructions bcis1 (which is the first induction hypothesis) and any arithmetic expression e2 (represented as e2) that was translated as the list of byte-code instructions bcis2 (which is the second induction hypothesis),
translating Plus (e1, e2) yields the list of byte-code instructions that begins with the instructions in bcis1, continues with the instructions in bcis2, and ends with the Add instruction
Remarks:
- translating e1 yields a list of byte-code instructions that is the prefix of the result of translating Plus (e1, e2); and
- the last instruction in the result of translating Plus (e1, e2) is Add.
induction step for subtractions:
for any arithmetic expression e1 (represented as e1) that was translated as the list of byte-code instructions bcis1 (which is the first induction hypothesis) and any arithmetic expression e2 (represented as e2) that was translated as the list of byte-code instructions bcis2 (which is the second induction hypothesis),
translating Minus (e1, e2) yields the list of byte-code instructions that begins with the instructions in bcis1, continues with the instructions in bcis2, and ends with the Sub instruction
induction step for quotients:
for any arithmetic expression e1 (represented as e1) that was translated as the list of byte-code instructions bcis1 (which is the first induction hypothesis) and any arithmetic expression e2 (represented as e2) that was translated as the list of byte-code instructions bcis2 (which is the second induction hypothesis),
translating Quotient (e1, e2) yields the list of byte-code instructions that begins with the instructions in bcis1, continues with the instructions in bcis2, and ends with the Quo instruction
induction step for remainders:
for any arithmetic expression e1 (represented as e1) that was translated as the list of byte-code instructions bcis1 (which is the first induction hypothesis) and any arithmetic expression e2 (represented as e2) that was translated as the list of byte-code instructions bcis2 (which is the second induction hypothesis),
translating Remainder (e1, e2) yields the list of byte-code instructions that begins with the instructions in bcis1, continues with the instructions in bcis2, and ends with the Rem instruction
Task 4¶
Implement a compiler from the source language to the target language as an OCaml function that satisfies the specification just above:
let compile (Source_program e) =
(* compile : source_program -> target_program *)
let rec translate e =
(* translate : arithmetic_expression -> byte_code_instruction list *)
...
in Target_program (translate e);;
This compiler should pass the unit tests.
Subsidiary questions:
- Does your compiler translate from left to right or from right to left?
- Does it make any observable difference whether your compiler translates from left to right or from right to left?
Task 5 (optional)¶
Presumably your compiler (in Task 4) uses list concatenation (i.e., List.append). List concatenation, however, incurs a linear cost since it prepends its first argument onto its second by copying it.
Program an alternative version of your compiler that does not use list concatenation (and verify that it passes the unit tests).
The capstone¶
We are now in position to test whether interpreting any given source program yields the same result as compiling this source program and running the resulting target program, i.e., whether the diagram above commutes:
let commutativity_test candidate_interpret candidate_compile candidate_run p =
(* commutativity_test : (source_program -> expressible_value) ->
(source_program -> target_program) ->
(target_program -> expressible_value) ->
source_program ->
bool *)
candidate_interpret p = candidate_run (candidate_compile p);;
Task 6¶
Implement a unit-test function to verify that interpreting source programs yields the same result as compiling them and running the resulting target programs.
Food for thought:
- The resource file for the present lecture note contains a generator of random arithmetic expressions, generate_random_arithmetic_expression that, given a non-negative integer n, yields a random arithmetic expression of depth at most n.
Subsidiary question:
What is the impact of
- evaluating from left to right vs. from right to left, and of
- translating from left to right vs. from right to left
on the commuting diagram? Does it always commute, no matter the order? If not, can you exhibit a counter-example? What is the consequence of this commutation or of this non-commutation?
Task 7 (optional)¶
Define the fold-right function associated with arithmetic_expression and use it to express both interpret (in Task 1) and compile (in Task 4).
Task 8 (meta-optional)¶
As a followup to Task 7 (optional), use the fold-right function associated with arithmetic_expression to express the compiler from Task 5 (optional).
Resources¶
- The complete OCaml code for the present lecture note (latest version: 04 Apr 2020).
Version¶
Created [04 Apr 2020]