Representing sets as lists

The goal of this lecture note is to study the representation of finite sets as the list of their elements without duplication, and to implement common set operations, as an unashamed excuse for writing structurally recursive functions over lists that compute set membership, set unions, set intersections, set differences, Cartesian products, and powersets.

Resources

• The OCaml code for the present lecture note (latest version: 20 Mar 2020).

A practical consideration

The order of elements does not matter, but in practice if the elements are ordered, it simplifies things to represent a set as the sorted list of its elements. So without loss of generality, henceforth we consider sets of integers, and we sort their representation in our unit tests.

Well-formed representation

A list represents a set if all of its elements only occur once:

let positive_test_is_set candidate =
  let b0 = (candidate [] = true)
  and b1 = (candidate [1; 2; 3] = true)
  and b2 = (candidate [1; 2; 3; 10] = true)
  and b3 = (candidate [1; 2; 3; 10; 20; 30] = true)
  (* etc *)
  in b0 && b1 && b2 && b3 (* etc. *);;

let negative_test_is_set candidate =
  let b0 = (candidate [1; 1] = false)
  and b1 = (candidate [1; 2; 3; 2] = false)
  (* etc *)
  in b0 && b1 (* etc. *);;

Inductively:

• base case:

  the empty list represents the empty set

• induction step:

  given an element v and a list vs’ that represents a set (which is the induction hypothesis), the list that starts with v and continues with vs represents a set if v does not occur in vs’

In OCaml, using a member function testing whether a given value occurs in a given list of values, and defined in the resource file:

let rec is_set vs =
  match vs with
  | [] ->
     true
  | v :: vs' ->
     if member v vs'
     then false
     else is_set vs';;

This function passes the unit tests:

# positive_test_is_set is_set;;
- : bool = true
# negative_test_is_set is_set;;
- : bool = true
#

Set membership

An element belongs to a set whenever its representation occurs in the representation of this set:

let belongs_to e es =
  member e es;;

So if e denote an element e and es the representation of a set s, evaluating belongs_to e es yields true whenever e belongs to s, and otherwise, it yields false.

Set inclusion

A set is included into another set whenever each of its elements belongs to this other set:

let positive_test_is_included_in candidate =
  let b0 = (candidate [] [0; 1; 2; 3; 4; 5] = true)
  and b1 = (candidate [1; 2; 3] [0; 1; 2; 3; 4; 5] = true)
  and b2 = (candidate [1; 2; 3] [0; 1; 3; 4; 2; 5] = true)
  (* etc *)
  in b0 && b1 (* etc. *);;

let negative_test_is_included_in candidate =
  let b0 = (candidate [1; 2; 3] [0; 1; 3; 4; 5] = false)
  (* etc *)
  in b0 (* etc. *);;

In the negative test, 2 does not belong to the set represented by [0; 1; 3; 4; 5].

Set inclusion is defined following the inductive structure of lists:

• base case:

  the empty set is included in all sets

• induction step:

  given an element e1 and two sets e1s' and e2s such that e1s' is included in e2s (which is the induction hypothesis),

  • if e1 belongs to e2s, then e1 :: e1s' is included in e2s
  • if e1 does not belong to e2s, then e1 :: e1s' is not included in e2s

In OCaml:

let is_included_in e1s e2s =
  let rec visit e1s =
    match e1s with
    | [] ->
       true
    | e1 :: e1s' ->
       if belongs_to e1 e2s
       then visit e1s'
       else false
  in visit e1s;;

This function passes the unit tests:

# positive_test_is_included_in is_included_in;;
- : bool = true
# negative_test_is_included_in is_included_in;;
- : bool = true
#

So if e1s and e2s denote the representation of two sets s1 and s2, evaluating is_included_in e1s e2s yields true whenever s1 is included in s2, and otherwise, it yields false.

It is simple to define the converse function:

let includes e2s e1s =
  is_included_in e1s e2s;;

Set equality

We simply define set equality as mutual set inclusion:

let set_equal e1s e2s =
  (is_included_in e1s e2s) && (includes e1s e2s);;

Adding an element to a set

Since a set is represented as a list of its elements without repetition, adding an element to a set is implemented as cons’ing it to the representation of this set if it does not already belongs to this set:

let set_add e es =
 (* set_add : 'a -> 'a list -> 'a list *)
  if belongs_to e es
  then es
  else e :: es;;

Creating a random set

Creating a random set is achieved by repeatedly applying set_add to a random number, starting with the representation of the empty set.

For example, creating a random set of size at most 3 is achieved by evaluating:

set_add (Random.int 1000)
        (set_add (Random.int 1000)
                 (set_add (Random.int 1000)
                          []))

Collecting random numbers in a list is of course a job for fold_right_nat, using the resident sorting function List.sort to make the result readable:

let make_random_set n =
  let () = assert (n >= 0) in
  List.sort (fun i j -> if i < j then 0 else 1)
            (fold_right_nat []
                            (fun ih -> set_add (Random.int 1000) ih)
                            n);;

The cardinality (i.e., number of elements) of the resulting set is 1 if all the instances of Random.int 1000 evaluate to the same random number, and it is more if several of these instances evaluate to distinct random numbers. To wit:

# make_random_set 0;;
- : int list = []
# make_random_set 1;;
- : int list = [740]
# make_random_set 2;;
- : int list = [546; 617]
# make_random_set 3;;
- : int list = [191; 519; 825]
# make_random_set 4;;
- : int list = [238; 805; 868; 898]
#

More forcefully, let us randomly generate 0 or 1 three times in a row to make the point:

# set_add (Random.int 2) (set_add (Random.int 2) (set_add (Random.int 2) []));;
- : int list = [0; 1]
# set_add (Random.int 2) (set_add (Random.int 2) (set_add (Random.int 2) []));;
- : int list = [1; 0]
# set_add (Random.int 2) (set_add (Random.int 2) (set_add (Random.int 2) []));;
- : int list = [1]
# set_add (Random.int 2) (set_add (Random.int 2) (set_add (Random.int 2) []));;
- : int list = [0]
#

Analysis:

1. In the first interaction, 0 was generated first, and then either 0 or 1, and then either 0 or 1.
2. In the second interaction, 1 was generated first, and then either 0 or 1, and then either 0 or 1.
3. In the third interaction, 1 was generated three times in a row.
4. In the fourth interaction, 0 was generated three times in a row.

Set union

The goal of this section is implement the traditional set union over the representations of sets.

Pictorially, given the two sets A and B,

and

that overlap like this,

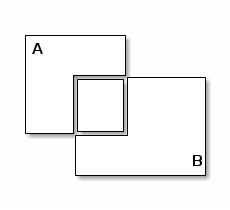
we want to compute their union, i.e., the following set:

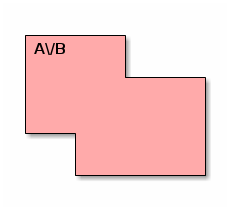
To this end, let us first specify the soundness and the completeness of the OCaml function set_union that implements set union.

For any set A (represented by e1s) and B (representing by e2s) such that A \/ B is the union of A and B, the result of evaluating set_union e1s e2s (let us call it e12s) represents a set:

• Soundness: e12s represents a set that is included in A \/ B, i.e., each element of the set represented by e12s either belongs to A or to B, or both.

  In words: each computed result is mathematically correct.

• Completeness: A \/ B is included in the set represented by e12s, i.e., all elements of A and B belong the set represented by e12s.

  In words: each mathematically correct result can be computed.

Extreme cases:

• a function mapping the representation of two sets to the representation of the empty set, i.e., fun e1s e2s -> [] is sound but not complete;
• functions mapping the representation of two sets to the representation of either set, i.e., fun e1s e2s -> e1s and fun e1s e2s -> e2s are sound but not complete;
• functions mapping the representation of two sets to the representation of a set where at least one element of either set is missing are sound but not complete; and
• a function mapping the representation of two sets to the representation of a set with extra elements (i.e., with at least one element not belonging to either of the two given sets) is complete but not sound.

(You can reflect on this soundness and completeness over the following particular cases:

• A and B are empty,
• A is empty but not B,
• B is empty but not A,
• A and B are not empty and they are disjoint,
• A and B are the same non-empty set, and
• A and B are not empty, not disjoint, and not the same.

These cases are exhaustive, and the last one is colorfully depicted above.)

In OCaml:

let soundness_of_set_union set_union e1s e2s =
  (* the resulting set only contains elements of e1s or e2s *)
  list_andmap
    (fun e12 -> belongs_to e12 e1s || belongs_to e12 e2s)
    (set_union e1s e2s);;

let completeness_of_set_union set_union e1s e2s =
  (* all elements of e1s and e2s occur in the resulting set *)
  let e12s = set_union e1s e2s
  in (list_andmap (fun e1 -> belongs_to e1 e12s) e1s) && (list_andmap (fun e2 -> belongs_to e2 e12s) e2s);;

These two tests are packaged together in one function that features useful error messages:

let soundness_and_completeness_of_set_union set_union e1s e2s =
  let sound = soundness_of_set_union set_union e1s e2s
              || let () = Printf.printf "soundness_of_set_union failed for %s and %s\n"
                                        (show_list show_int e1s)
                                        (show_list show_int e2s)
                 in false
  and complete = completeness_of_set_union set_union e1s e2s
                 || let () = Printf.printf "completeness_of_set_union failed for %s and %s\n"
                                           (show_list show_int e1s)
                                           (show_list show_int e2s)
                    in false
  in sound && complete;;

And we are now in position to write a traditional unit-test function, first on a handful of intuitive tests, and then on random sets:

let test_set_union candidate =
  let b0 = soundness_and_completeness_of_set_union candidate [] []
  and b1 = (soundness_and_completeness_of_set_union candidate [] [0; 1; 2; 3; 4; 5])
           &&
           (soundness_and_completeness_of_set_union candidate [0; 1; 2; 3; 4; 5] [])
  and b2 = soundness_and_completeness_of_set_union candidate [0; 1; 2; 3; 4; 5] [0; 1; 2; 3; 4; 5]
  and b3 = (soundness_and_completeness_of_set_union candidate [1; 2; 3] [0; 4; 5])
           &&
           (soundness_and_completeness_of_set_union candidate [0; 4; 5] [1; 2; 3])
  and b4 = (soundness_and_completeness_of_set_union candidate [0; 1; 2; 3; 4; 5] [3; 4; 5; 6; 7])
           &&
           (soundness_and_completeness_of_set_union candidate [3; 4; 5; 6; 7] [0; 1; 2; 3; 4; 5])
  and b5 = let es1 = make_random_set 100
           and es2 = make_random_set 100
           in (soundness_and_completeness_of_set_union candidate es1 es2)
              &&
              (soundness_and_completeness_of_set_union candidate es2 es1)
  and b6 = let es1 = make_random_set 100
           and es2 = make_random_set 100
           in (soundness_and_completeness_of_set_union candidate es1 es2)
              &&
              (soundness_and_completeness_of_set_union candidate es2 es1)
  and b7 = let es1 = make_random_set 100
           and es2 = make_random_set 100
           in (soundness_and_completeness_of_set_union candidate es1 es2)
              &&
              (soundness_and_completeness_of_set_union candidate es2 es1)
  (* etc. *)
  in b0 && b1 && b2 && b3 && b4 && b5 && b6 && b7 (* etc. *);;

Exercise 4

Program a function set_union such that if e1s and e2s denote the representation of two sets s1 and s2, evaluating set_union e1s e2s yields the representation of the union of s1 and s2.

Here is an inductive specification of set union (that verbs the noun “union”, just wheel with it). Given a set s2 represented by e2s,

• base case: unioning the empty set (represented by the empty list []) with s2 (represented by e2s) yields s2
• induction step: given a set s1’ (represented by e1s') such that unioning it with s2 (represented by e2s') yields the set s1’ \/ s2 (which is the induction hypothesis) and given an element e1 (represented by e1) that does not belong to s1’,
  • if e1 belongs to s2 then unioning {e1} \/ s1’ (represented by e1 :: e1s') with s2 yields s1’ \/ s2, and
  • if e1 does not belong to s2 then unioning {e1} \/ s1’ (represented by e1 :: e1s') with s2 yields {e1} \/ (s1’ \/ s2).

Solution for Exercise 4

Since set union is specified by structural induction over the first set, it is implemented with an OCaml function that is structurally recursive over its first argument:

let set_union_v0 e1s e2s =
  let rec visit e1s =
    match e1s with
    | [] ->
       e2s
    | e1 :: e1s' ->
       if belongs_to e1 e2s
       then visit e1s'
       else e1 :: visit e1s'
  in visit e1s;;

Rationale:

• in the base case, the result is e2s, and
• in the induction step, where the induction hypothesis is implemented by the recursive call, we use an if-expression to distinguish whether the current first element of the list representing the first set (which does not occur in the rest of the list because the given lists are well-formed representations of two sets) occurs in the second set.

This implementation passes our unit tests:

# test_set_union set_union_v0;;
- : bool = true
#

First interlude

Harald: The pattern of recursion in the definition of set_union_v0 is interesting.

Alfrothul: Now what.

Harald: In the if-expression, the consequent contains a tail call and the alternative contains a non-tail call.

Alfrothul: OK?

Harald: So tracing these calls should give rise to pretty patterns.

Alfrothul: We’re in luck, the resource file contains a traced version. Let me try:

# traced_set_union_v0 show_int [1; 2; 3] [4; 5; 6];;
set_union_v0 [1; 2; 3] [4; 5; 6] ->
  visit [1; 2; 3] ->
    visit [2; 3] ->
      visit [3] ->
        visit [] ->
        visit [] <- [4; 5; 6]
      visit [3] <- [3; 4; 5; 6]
    visit [2; 3] <- [2; 3; 4; 5; 6]
  visit [1; 2; 3] <- [1; 2; 3; 4; 5; 6]
set_union_v0 [1; 2; 3] [4; 5; 6] <- [1; 2; 3; 4; 5; 6]
- : int list = [1; 2; 3; 4; 5; 6]
#

Alfrothul: That looks pretty standard – a bunch of nested calls, and the corresponding bunch of returns. Kind of like append.

Brynja: Actually, exactly like append, since the sets {1, 2, 3} and {4, 5, 6} don’t intersect.

Alfrothul: True.

Harald: Right. But what if they intersect, like, completely:

# traced_set_union_v0 show_int [1; 2; 3] [1; 2; 3];;
set_union_v0 [1; 2; 3] [1; 2; 3] ->
  visit [1; 2; 3] ->
  visit [2; 3] ->
  visit [3] ->
  visit [] ->
  visit [] <- [1; 2; 3]
set_union_v0 [1; 2; 3] [1; 2; 3] <- [1; 2; 3]
- : int list = [1; 2; 3]
#

Alfrothul: Wow. An iterative computation. Harald, you deserve an award.

Harald: We all got one already, but thanks.

Vigfus: No semiotics, please, no semiotics, OK?

Brynja: What if the first set is included in the second one? Lemmesee:

# traced_set_union_v0 show_int [1; 3; 5] [1; 2; 3; 4; 5; 6];;
set_union_v0 [1; 3; 5] [1; 2; 3; 4; 5; 6] ->
  visit [1; 3; 5] ->
  visit [3; 5] ->
  visit [5] ->
  visit [] ->
  visit [] <- [1; 2; 3; 4; 5; 6]
set_union_v0 [1; 3; 5] [1; 2; 3; 4; 5; 6] <- [1; 2; 3; 4; 5; 6]
- : int list = [1; 2; 3; 4; 5; 6]
#

Brynja: Yup, iteration.

Vigfus: And what if the second set is included in the first one? Like, with your example, Brynja, but swapped:

# traced_set_union_v0 show_int [1; 2; 3; 4; 5; 6] [1; 3; 5];;
set_union_v0 [1; 2; 3; 4; 5; 6] [1; 3; 5] ->
  visit [1; 2; 3; 4; 5; 6] ->
  visit [2; 3; 4; 5; 6] ->
    visit [3; 4; 5; 6] ->
    visit [4; 5; 6] ->
      visit [5; 6] ->
      visit [6] ->
        visit [] ->
        visit [] <- [1; 3; 5]
      visit [6] <- [6; 1; 3; 5]
    visit [4; 5; 6] <- [4; 6; 1; 3; 5]
  visit [2; 3; 4; 5; 6] <- [2; 4; 6; 1; 3; 5]
set_union_v0 [1; 2; 3; 4; 5; 6] [1; 3; 5] <- [2; 4; 6; 1; 3; 5]
- : int list = [2; 4; 6; 1; 3; 5]
#

Vigfus: Funny pattern.

Brynja: Right. Every time an element of the first set occurs in the second, there is a tail call, so there is no indentation, and every time an element of the first set does not occur in the second, there is a non-tail call, so there is an indentation. The following example should illustrate this point:

# traced_set_union_v0 show_int [1; 2; 3; 4; 5; 6; 7; 8; 9] [1; 2; 3; 7; 8; 9];;
set_union_v0 [1; 2; 3; 4; 5; 6; 7; 8; 9] [1; 2; 3; 7; 8; 9] ->
  visit [1; 2; 3; 4; 5; 6; 7; 8; 9] ->
  visit [2; 3; 4; 5; 6; 7; 8; 9] ->
  visit [3; 4; 5; 6; 7; 8; 9] ->
  visit [4; 5; 6; 7; 8; 9] ->
    visit [5; 6; 7; 8; 9] ->
      visit [6; 7; 8; 9] ->
        visit [7; 8; 9] ->
        visit [8; 9] ->
        visit [9] ->
        visit [] ->
        visit [] <- [1; 2; 3; 7; 8; 9]
      visit [6; 7; 8; 9] <- [6; 1; 2; 3; 7; 8; 9]
    visit [5; 6; 7; 8; 9] <- [5; 6; 1; 2; 3; 7; 8; 9]
  visit [4; 5; 6; 7; 8; 9] <- [4; 5; 6; 1; 2; 3; 7; 8; 9]
set_union_v0 [1; 2; 3; 4; 5; 6; 7; 8; 9] [1; 2; 3; 7; 8; 9] <- [4; 5; 6; 1; 2; 3; 7; 8; 9]
- : int list = [4; 5; 6; 1; 2; 3; 7; 8; 9]
#

Vigfus: So there is as many recursive calls as there are elements in the first set that do not occur in the second set.

Brynja: Precisely.

Second interlude

Vifgus: Why are we not using set_add in the definition of set_union?

Harald: Good point! The specification would be simpler:

• base case: unioning the empty set (represented by the empty list []) with s2 (represented by e2s) yields s2
• induction step: given a set s1’ (represented by e1s') such that unioning it with s2 (represented by e2s') yields the set s1’ \/ s2 (which is the induction hypothesis) and given an element e1 (represented by e1) that does not belong to s1’, unioning {e1} U s1’ (represented by e1 :: e1s') with s2 yields {e1} \/ (s1’ \/ s2).

Loki: Lucky us that set union is associative.

Alfrothul: Er... Yes, I guess, and the implementation is simpler too:

let set_union_v1 e1s e2s =
  let rec visit e1s =
    match e1s with
    | [] ->
       e2s
    | e1 :: e1s' ->
       set_add e1 (visit e1s')
  in visit e1s;;

Vigfus: And it passes the unit test too:

# test_set_union set_union_v1;;
- : bool = true
#

Brynja: But it incurs more recursive calls: in the definition of set_union_v0, belongs_to is called for each element of e1s and each time, it traverses e2s, whereas here, belongs_to is also called for each element of e1s but each time, it traverses e2s as well as every element that is prepended to it in order to construct the union.

Alfrothul: So set_union_v1 is faithful to the set-theoretical specification of union (the “what”)...

Harald: ...and set_union_v0 exploits the representation of sets as lists of their elements (the “how”).

Mimer: The art of Computer Science.

Loki: You guys are going to love Exercise 16.

Exercise 5

Exhibit two sets s1 (represented by e1s) and s2 (represented by e2s) such that evaluating trace_set_union show_int e1s e2s emits a trace

• that starts with 5 tail calls,
• that continues with 3 non-tail calls,
• that continues with 3 tail calls, and then
• that finishes with a series of returns.

Justify your solution. (And also: how many returns will there be?)

Set intersection

The goal of this section is implement the traditional set intersection over the representations of sets.

Pictorially, given the same two sets A and B,

and

that overlap like this,

we want to compute their intersection, i.e., the following set:

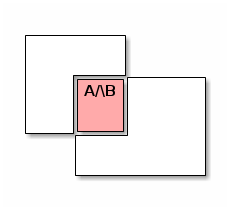
To this end, let us first specify the soundness and the completeness of the OCaml function set_intersection that implements set intersection.

For any set A (represented by e1s) and B (representing by e2s) such that A /\ B is the intersection of A and B, the result of evaluating set_intersection e1s e2s (let us call it e12s) represents a set:

• Soundness: e12s represents a set that is included in A /\ B, i.e., each element of the set represented by e12s both belongs to A and to B.

  In words: each computed result is mathematically correct.

• Completeness: A /\ B is included in the set represented by e12s, i.e., all elements that belong both to A and to B belong to the set represented by e12s.

  In words: each mathematically correct result can be computed.

Extreme cases:

• a function mapping the representation of two sets to the representation of the empty set, i.e., fun e1s e2s -> [] is sound but not complete;
• functions mapping the representation of two sets to the representation of a set where at least one element of both sets is missing are sound but not complete; and
• a function mapping the representation of two sets to the representation of a set with extra elements (i.e., at least one element not belonging to both the two given sets) is complete but not sound.

(You can reflect on this soundness and completeness over the following particular cases:

• A and B are empty,
• A is empty but not B,
• B is empty but not A,
• A and B are not empty and they are disjoint,
• A and B are the same non-empty set, and
• A and B are not empty, not disjoint, and not the same.

These cases are exhaustive, and the last one is colorfully depicted above.)

In OCaml:

let soundness_of_set_intersection set_intersection e1s e2s =
  (* the resulting set only contains elements of e1s and e2s *)
  list_andmap
    (fun e12 -> belongs_to e12 e1s && belongs_to e12 e2s)
    (set_intersection e1s e2s);;

let completeness_of_set_intersection set_intersection e1s e2s =
  (* all common elements of e1s and e2s occur in the resulting set *)
  let e12s = set_intersection e1s e2s
  in list_andmap
       (fun e1 -> if belongs_to e1 e2s
                  then belongs_to e1 e12s
                  else true)
       e1s;;

These two tests are packaged together in one function that features useful error messages:

let soundness_and_completeness_of_set_intersection set_intersection e1s e2s =
  let sound = soundness_of_set_intersection set_intersection e1s e2s
              || let () = Printf.printf "soundness_of_set_intersection failed for %s and %s\n"
                                        (show_list show_int e1s)
                                        (show_list show_int e2s)
                 in false
  and complete = completeness_of_set_intersection set_intersection e1s e2s
                 || let () = Printf.printf "completeness_of_set_intersection failed for %s and %s\n"
                                           (show_list show_int e1s)
                                           (show_list show_int e2s)
                    in false
  in sound && complete;;

And we are now in position to write a traditional unit-test function, first on a handful of intuitive tests, and then on random sets:

let test_set_intersection candidate =
  let b0 = soundness_and_completeness_of_set_intersection candidate [] []
  and b1 = (soundness_and_completeness_of_set_intersection candidate [] [0; 1; 2; 3; 4; 5])
           &&
           (soundness_and_completeness_of_set_intersection candidate [0; 1; 2; 3; 4; 5] [])
  and b2 = soundness_and_completeness_of_set_intersection candidate [0; 1; 2; 3; 4; 5] [0; 1; 2; 3; 4; 5]
  and b3 = (soundness_and_completeness_of_set_intersection candidate [1; 2; 3] [0; 4; 5])
           &&
           (soundness_and_completeness_of_set_intersection candidate [0; 4; 5] [1; 2; 3])
  and b4 = (soundness_and_completeness_of_set_intersection candidate [0; 1; 2; 3; 4; 5] [3; 4; 5; 6; 7])
           &&
           (soundness_and_completeness_of_set_intersection candidate [3; 4; 5; 6; 7] [0; 1; 2; 3; 4; 5])
  and b5 = let es1 = make_random_set 100
           and es2 = make_random_set 100
           in (soundness_and_completeness_of_set_intersection candidate es1 es2)
              &&
              (soundness_and_completeness_of_set_intersection candidate es2 es1)
  and b6 = let es1 = make_random_set 100
           and es2 = make_random_set 100
           in (soundness_and_completeness_of_set_intersection candidate es1 es2)
              &&
              (soundness_and_completeness_of_set_intersection candidate es2 es1)
  and b7 = let es1 = make_random_set 100
           and es2 = make_random_set 100
           in (soundness_and_completeness_of_set_intersection candidate es1 es2)
              &&
              (soundness_and_completeness_of_set_intersection candidate es2 es1)
  (* etc. *)
  in b0 && b1 && b2 && b3 && b4 && b5 && b6 && b7 (* etc. *);;

Exercise 6

Program a function set_intersection such that if e1s and e2s denote the representation of two sets s1 and s2, evaluating set_intersection e1s e2s yields the representation of the intersection of s1 and s2.

Here is an inductive specification of set intersection. Given a set s2 represented by e2s,

• base case: intersecting the empty set (represented by the empty list []) with s2 (represented by e2s) yields the empty set
• induction step: given a set s1’ (represented by e1s') such that intersecting it with s2 (represented by e2s') yields the set s1’ /\ s2 (which is the induction hypothesis) and given an element e1 (represented by e1) that does not belong to s1’,
  • if e1 belongs to s2 then intersecting {e1} \/ s1’ (represented by e1 :: e1s') with s2 yields {e1} \/ (s1’ /\ s2), and
  • if e1 does not belong to s2 then unioning {e1} \/ s1’ (represented by e1 :: e1s') with s2 yields s1’ /\ s2.

Solution for Exercise 6

Since set intersection is specified by structural induction over the first set, it is implemented with an OCaml function that is structurally recursive over its first argument:

let set_intersection_v0 e1s e2s =
  let rec visit e1s =
    match e1s with
    | [] ->
       []
    | e1 :: e1s' ->
       if belongs_to e1 e2s
       then e1 :: visit e1s'
       else visit e1s'
  in visit e1s;;

Rationale:

• in the base case, the result is [], and
• in the induction step, where the induction hypothesis is implemented by the recursive call, we use an if-expression to distinguish whether the current first element of the list representing the first set (which does not occur in the rest of the list because the given lists are well-formed representations of two sets) occurs in the second set.

This implementation passes our unit tests:

# test_set_intersection set_intersection_v0;;
- : bool = true
#

Exercise 7

Could we use set_add in the definition of set_intersection?

Exercise 8

Exhibit two sets s1 (represented by e1s) and s2 (represented by e2s) such that evaluating trace_set_intersection show_int e1s e2s (available in the accompanying resource file) emits a trace

• that starts with 5 tail calls,
• that continues with 3 non-tail calls,
• that continues with 3 tail calls, and then
• that finishes with a series of returns.

Justify your solution. (And also: how many returns will there be?)

Hint: read the First interlude.

Set difference

The goal of this section is to implement the traditional set difference over the representations of sets.

Again, given the same two sets A and B,

and

that overlap like this,

we want to compute their difference, i.e., the following set:

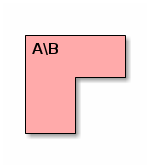
To this end, let us first specify the soundness and the completeness of the OCaml function set_minus that implements set difference.

For any set A (represented by e1s) and B (representing by e2s) such that A \ B is the set difference of A and B, the result of evaluating set_minus e1s e2s (let us call it e12s) represents a set:

• Soundness: e12s represents a set that is included in A \ B, i.e., each element of the set represented by e12s belongs to A but not to B.

  In words: each computed result is mathematically correct.

• Completeness: A \ B is included in the set represented by e12s, i.e.,

  • each element of the set represented by e1s that does not belong to the set represented by e2s belongs to the set represented by e12s and
  • each element of the set represented by e2s does not belong to the set represented by e12s.

  In words: each mathematically correct result can be computed.

Extreme cases:

• a function mapping the representation of two sets to the representation of the empty set, i.e., fun e1s e2s -> [] is sound but not complete;
• functions mapping the representation of two sets to the representation of a set where at least one element of the first set is missing are sound but not complete; and
• a function mapping the representation of two sets to the representation of a set with extra elements (i.e., at least one element not belonging to both the two given sets) is complete but not sound.

(You can reflect on this soundness and completeness over the following particular cases:

• A and B are empty,
• A is empty but not B,
• B is empty but not A,
• A and B are not empty and they are disjoint,
• A and B are the same non-empty set, and
• A and B are not empty, not disjoint, and not the same.

These cases are exhaustive, and the last one is colorfully depicted above.)

In OCaml:

let soundness_of_set_minus set_minus e1s e2s =
  (* the resulting set only contains elements of e1s that do not occur in e2s *)
  list_andmap
    (fun e12 -> belongs_to e12 e1s && not (belongs_to e12 e2s))
    (set_minus e1s e2s);;

let completeness_of_set_minus set_minus e1s e2s =
  (* all elements of e1s and not of e2s occur in the resulting set
     and
     no element of e2s occurs in the resulting set *)
  let e12s = set_minus e1s e2s
  in (list_andmap
        (fun e1 -> if not (belongs_to e1 e2s)
                   then belongs_to e1 e12s
                   else true)
        e1s
     &&
     (list_andmap
       (fun e2 -> not (belongs_to e2 e12s))
       e2s);;

These two tests are packaged together in one function that features useful error messages:

let soundness_and_completeness_of_set_minus set_minus e1s e2s =
  let sound = soundness_of_set_minus set_minus e1s e2s
              || let () = Printf.printf "soundness_of_set_minus failed for %s and %s\n"
                                        (show_list show_int e1s)
                                        (show_list show_int e2s)
                 in false
  and complete = completeness_of_set_minus set_minus e1s e2s
                 || let () = Printf.printf "completeness_of_set_minus failed for %s and %s\n"
                                           (show_list show_int e1s)
                                           (show_list show_int e2s)
                    in false
  in sound && complete;;

And we are now in position to write a traditional unit-test function, first on a handful of intuitive tests, and then on random sets:

let test_set_minus candidate =
  let b0 = soundness_and_completeness_of_set_minus candidate [] []
  and b1 = (soundness_and_completeness_of_set_minus candidate [] [0; 1; 2; 3; 4; 5])
           &&
           (soundness_and_completeness_of_set_minus candidate [0; 1; 2; 3; 4; 5] [])
  and b2 = soundness_and_completeness_of_set_minus candidate [0; 1; 2; 3; 4; 5] [0; 1; 2; 3; 4; 5]
  and b3 = (soundness_and_completeness_of_set_minus candidate [1; 2; 3] [0; 4; 5])
           &&
           (soundness_and_completeness_of_set_minus candidate [0; 4; 5] [1; 2; 3])
  and b4 = (soundness_and_completeness_of_set_minus candidate [0; 1; 2; 3; 4; 5] [3; 4; 5; 6; 7])
           &&
           (soundness_and_completeness_of_set_minus candidate [3; 4; 5; 6; 7] [0; 1; 2; 3; 4; 5])
  and b5 = let es1 = make_random_set 100
           and es2 = make_random_set 100
           in (soundness_and_completeness_of_set_minus candidate es1 es2)
              &&
              (soundness_and_completeness_of_set_minus candidate es2 es1)
  and b6 = let es1 = make_random_set 100
           and es2 = make_random_set 100
           in (soundness_and_completeness_of_set_minus candidate es1 es2)
              &&
              (soundness_and_completeness_of_set_minus candidate es2 es1)
  and b7 = let es1 = make_random_set 100
           and es2 = make_random_set 100
           in (soundness_and_completeness_of_set_minus candidate es1 es2)
              &&
              (soundness_and_completeness_of_set_minus candidate es2 es1)
  (* etc. *)
  in b0 && b1 && b2 && b3 && b4 && b5 && b6 && b7 (* etc. *);;

Exercise 9

Program a function set_minus such that if e1s and e2s denote the representation of two sets s1 and s2, evaluating set_minus e1s e2s yields the representation of the difference between s1 and s2.

Here is an inductive specification of set difference. Given a set s2 represented by e2s,

• base case: subtracting s2 (represented by e2s) to the empty set (represented by the empty list []) yields the empty set
• induction step: given a set s1’ (represented by e1s') such that subtracting s2 (represented by e2s') to it yields the set s1’ \ s2 (which is the induction hypothesis) and given an element e1 (represented by e1) that does not belong to s1’,
  • if e1 belongs to s2 then subtracting s2 to {e1} \/ s1’ (represented by e1 :: e1s') yields s1’ \ s2, and
  • if e1 does not belong to s2 then subtracting s2 to {e1} \/ s1’ (represented by e1 :: e1s') yields {e1} \/ (s1’ \ s2).

Solution for Exercise 9

Since set difference is specified by structural induction over the first set, it is implemented with an OCaml function that is structurally recursive over its first argument:

let set_minus_v0 e1s e2s =
  let rec visit e1s =
    match e1s with
    | [] ->
       []
    | e1 :: e1s' ->
       if belongs_to e1 e2s
       then visit e1s'
       else e1 :: visit e1s'
  in visit e1s;;

Rationale:

• in the base case, the result is [], and
• in the induction step, where the induction hypothesis is implemented by the recursive call, we use an if-expression to distinguish whether the current first element of the list representing the first set (which does not occur in the rest of the list because the given lists are well-formed representations of two sets) occurs in the second set.

This implementation passes our unit tests:

# test_set_minus set_minus_v0;;
- : bool = true
#

Subsidiary question: could we use set_add in the definition of set_minus?

Exercise 10

Exhibit two sets s1 (represented by e1s) and s2 (represented by e2s) such that evaluating trace_set_minus show_int e1s e2s (available in the accompanying resource file) emits a trace

• that starts with 5 tail calls,
• that continues with 3 non-tail calls,
• that continues with 3 tail calls, and then
• that finishes with a series of returns.

Justify your solution. (And also: how many returns will there be?)

Exercise 11

Use set-theoretic identities such as for any sets A and B,

• the intersection of [the union of A and B] and A is A,
• the intersection of [the union of A and B] and B is B,
• the difference between A and B is included in A,
• the intersection between [the difference between A and B] and B is empty,
• etc.

to beef up the unit-tests above.

For example:

let beefed_up_test set_union set_intersection set_minus =
  let e0s = [0; 1; 2; 3; 4; 5; 6; 7; 8]
  and e1s = [1; 3; 5; 7]
  and e2s = [2; 4; 6; 8]
  in let b0 = (set_equal (set_intersection (set_union e0s e1s) e0s)
                         e0s)
     and b1 = (set_equal (set_intersection (set_union e0s e1s) e1s)
                         e1s)
     and b2 = (is_included_in (set_minus e0s e1s) e0s)
     (* etc. *)
     in b0 && b1 && b2 (* etc. *);;

Exercise 12

Specify and implement the traditional symmetric difference over the representations of sets.

Normalizing a list into the representation of a set

Since a list represents a set when it contains no repeated element, it is simple to normalize a list so that it represents a set: just remove its repeated elements.

The unit test is simple to write:

let test_normalize_list_into_set candidate =
  let b0 = (is_set (candidate [1; 2; 3; 4]))
  and b1 = (is_set (candidate [1; 1; 1; 1]))
  and b2 = (is_set (candidate []))
  and b3 = (is_set (candidate [1; 2; 3; 4; 3; 2; 1]))
  (* etc. *)
  in b0 && b1 && b2 && b3 (* etc. *);;

Normalization is defined following the inductive structure of lists:

• base case:

  the empty list is well formed (and represents the empty set)

• induction step:

  given an element v and a list vs' that represents a set, i.e., that is a list of elements without repetition (which is the induction hypothesis),

  • if v occurs in vs', v :: vs' does not represent a set (but vs' does)
  • if v does not occur in vs', v :: vs' represents a set

In OCaml:

let rec normalize_list_into_set vs =
  match vs with
  | [] ->
     []
  | v :: vs' ->
     if member v vs'
     then normalize_list_into_set vs'
     else v :: normalize_list_into_set vs';;

This definition passes the unit test:

# test_normalize_list_into_set normalize_list_into_set;;
- : bool = true
#

Exercise 13

Consider the following implementation of set union:

let set_union_quick_and_dirty e1s e2s =
  normalize_list_into_set (e1s @ e2s);;

where @ is the infix notation for list concatenation:

let set_union_quick_and_dirty' e1s e2s =
  normalize_list_into_set (List.append e1s e2s);;

Do you think that this implementation does the job? Does it pass the unit tests, for example? What do you make of that?

Solution for Exercise 13

• Yes, this implementation does the job in practice: concatenating the two given lists yields a list of all the elements, possibly with repetitions, and normalizing this list removes these repetitions.

• It does pass the unit tests:

  # test_set_union set_union_quick_and_dirty;;
  - : bool = true
  #
  

• This implementation works in practice but it steps out of the model, since it constructs an intermediate list that does not represent a set. Also, it is less efficient than the implementation in the solution for Exercise 4 in that it checks whether each element of the intermediate list occurs in the rest of this intermediate list, whereas the implementation in the solution for Exercise 4 only checks whether each element of the first list occurs in the second list.

Exercise 14

As is well known, your friendly Nordic deity, Loki, lives and breathes outside the box. This morning, he suggested the following radical implementation of set union:

let set_union_outside_the_box e1s e2s =
  e1s @ e2s;;

Do you think that this function does the job? Does it pass the unit tests, for example? What do you make of that?

Solution for Exercise 14

• No, this implementation does not do the job: concatenating the two given lists yields a list of all the elements, possibly with repetitions, and therefore the resulting list does not represent a set in general.

• It does, however, pass the unit tests:

  # test_set_union set_union_outside_the_box;;
  - : bool = true
  #
  

• The fact that this incorrect implementation passes the unit test alerts us to the fact that the soundness function does not check that the candidate set-union function yields a well-formed set. It should be vigilantly amended as follows:

  let soundness_of_set_union set_union e1s e2s =
    (* the resulting set is well formed and only contains elements of e1s or e2s *)
    let e12s = set_union e1s e2s
    in is_set e12s && list_andmap (fun e12 -> belongs_to e12 e1s || belongs_to e12 e2s) e12s;;
  

  The reader is invited

  • to check that with this amended definition, set_union_outside_the_box fails the unit tests, and
  • to ponder whether soundness_of_set_intersection and soundness_of_set_minus need a similarly vigilant amendment.

Vigfus: So we should do like Loki?

Harald: Beg pardon?

Vigfus: We should start by devising an OCaml function set_intersection_outside_the_box?

Alfrothul: I guess we should.

Harald: Let’s see. This function should radically compute a list of elements of an intersection...

Alfrothul: ...with duplications.

Vigfus: This radical implementation ought to pass the unit tests.

Brynja: And then we should amend soundness_of_set_intersection.

Harald: Vigilantly.

Vigfus: And then the radical implementation should fail the unit tests.

Loki: You guys will make wonderful consultants.

Computing the Cartesian product of two sets

The Cartesian product of two sets A and B is the set of pairs whose first component belongs to A and whose second component belongs to B:

A * B = {(a, b) | (a belongs to A) and (b belongs to B)}

Assuming that a set is represented as the list of its elements, without duplication, and that the Cartesian product is constructed from left to right (whatever that means, see just below), here is a series of observations, starting with the fact that the cardinality (i.e., number of elements) of a Cartesian product is the product of the cardinality of these sets:

• the Cartesian product of the empty set and any set is empty;
• the Cartesian product of two singleton sets is a singleton set whose element pairs the elements of the singleton sets;
• constructing the Cartesian product from left to right means enumerating the elements of the first set from left to right, and, for each of these elements, enumerating the elements of the second set from left to right.

These observations sum up to the following unit-test function, indenting the expected result of the candidate function to reflect the left-to-right enumeration:

let test_cartesian_product_2 candidate =
  let b0a = (candidate []
                       []
             = [])
  and b1a = (candidate [1]
                       []
             = [])
  and b1b = (candidate [2; 1]
                       []
             = [])
  and b1c = (candidate []
                       [10]
             = [])
  and b1d = (candidate []
                       [20; 10]
             = [])
  and b2a = (candidate [1]
                       [10]
             = [(1, 10)])
  and b2b = (candidate [2; 1]
                       [10]
             = [(2, 10); (1, 10)])
  and b2c = (candidate [3; 2; 1]
                       [10]
             = [(3, 10); (2, 10); (1, 10)])
  and b3a = (candidate [1]
                       [20; 10]
             = [(1, 20); (1, 10)])
  and b3b = (candidate [2; 1]
                       [20; 10]
             = [(2, 20); (2, 10);
                (1, 20); (1, 10)])
  and b3c = (candidate [3; 2; 1]
                       [20; 10]
             = [(3, 20); (3, 10);
                (2, 20); (2, 10);
                (1, 20); (1, 10)])
  and b3d = (candidate [4; 3; 2; 1]
                       [20; 10]
             = [(4, 20); (4, 10);
                (3, 20); (3, 10);
                (2, 20); (2, 10);
                (1, 20); (1, 10)])
  and b4a = (candidate [1]
                       [30; 20; 10]
             = [(1, 30); (1, 20); (1, 10)])
  and b4b = (candidate [2; 1]
                       [30; 20; 10]
             = [(2, 30); (2, 20); (2, 10);
                (1, 30); (1, 20); (1, 10)])
  and b4c = (candidate [3; 2; 1]
                       [20; 10]
             = [(3, 20); (3, 10);
                (2, 20); (2, 10);
                (1, 20); (1, 10)])
  and b4d = (candidate [4; 3; 2; 1]
                       [20; 10]
             = [(4, 20); (4, 10);
                (3, 20); (3, 10);
                (2, 20); (2, 10);
                (1, 20); (1, 10)])
  and b5a = (candidate [4; 3; 2; 1]
                       [30; 20; 10]
             = [(4, 30); (4, 20); (4, 10);
                (3, 30); (3, 20); (3, 10);
                (2, 30); (2, 20); (2, 10);
                (1, 30); (1, 20); (1, 10)])
  (* etc. *)
  in b0a && b1a && b1b && b1c && b1d && b2a && b2b && b2c && b3a && b3b && b3c && b3d && b4a && b4b && b4c && b4d && b5a (* etc. *);;

Given two lists vs_init and ws_init, let us follow their inductive structure to specify two auxiliary functions:

• the first one, traverse_1, is defined over the structure of vs_init, and for each of its elements,
  • the second one, traverse_2 is defined over the structure of ws_init.

So traverse_2 is defined locally to traverse_1. To exemplify this nesting, we refer to the inductive specification of traverse_1 as the outer one, and to the inductive specification of traverse_2 as the inner one. The outer function is specified by induction over a list vs, which is initialized with vs_init, and the inner one is specified by induction over a list ws, which is initialized with ws_init:

• outer base case (vs = []):

  the Cartesian product of the empty set and ws_init is the empty set

• outer induction step (vs = v :: vs’):

  assuming that traverse_1 maps vs’ to vs’_and_ws_init_with_pairs_prepended (which is the outer induction hypothesis), let us follow the inductive structure of lists to specify traverse_2, whose job is to prepend pairs with v as their first component to vs’_and_ws_init_with_pairs_prepended; the second component of these successive pairs is each successive element of ws_init:

  • inner base case (ws = []):

    there is nothing to prepend, and so the result is vs’_and_ws_init_with_pairs_prepended

  • inner induction step (ws = w :: ws’):

    assuming that traverse_2 maps ws’ to vs’_and_ws’_with_pairs_prepended (which is the inner induction hypothesis), it should map w :: ws’ to the list (v, w) :: vs’_and_ws’_with_pairs_prepended

Remark:

• in the outer induction step, vs’_and_ws_init_with_pairs_prepended is the Cartesian product of vs’ and ws_init.

In OCaml:

let cartesian_product_2 vs_init ws_init =
  let rec traverse_1 vs =
    match vs with
    | [] ->
       []
    | v :: vs' ->
       let vs'_and_ws_init_with_pairs_prepended = traverse_1 vs'
       in let rec traverse_2 ws =
            match ws with
            | [] ->
               vs'_and_ws_init_with_pairs_prepended
            | w :: ws' ->
               let vs'_and_ws'_with_pairs_prepended = traverse_2 ws'
               in (v, w) :: vs'_and_ws'_with_pairs_prepended
          in traverse_2 ws_init
  in traverse_1 vs_init;;

Analysis:

• cartesian_product_2 is not defined recursively;
• traverse_1 is defined locally to cartesian_product_2;
• traverse_1 is defined recursively, and its recursive call implements the outer induction hypothesis;
• traverse_2 is defined locally to traverse_1;
• traverse_2 is defined recursively, and its recursive call implements the inner induction hypothesis.

This OCaml function passes the unit test:

# test_cartesian_product_2 cartesian_product_2;;
- : bool = true
#

Traced versions of traverse_1 and traverse_2 (defined in the resource file for the present lecture note) make it possible to visualize the traversals of vs_init and ws_init:

# traced_cartesian_product_2 [3; 2; 1] [40; 30; 20; 10];;
traverse_1 [3; 2; 1] ->
  traverse_1 [2; 1] ->
    traverse_1 [1] ->
      traverse_1 [] ->
      traverse_1 [] <- []
      traverse_2 [40; 30; 20; 10] ->
        traverse_2 [30; 20; 10] ->
          traverse_2 [20; 10] ->
            traverse_2 [10] ->
              traverse_2 [] ->
              traverse_2 [] <- []
            traverse_2 [10] <- [(1, 10)]
          traverse_2 [20; 10] <- [(1, 20); (1, 10)]
        traverse_2 [30; 20; 10] <- [(1, 30); (1, 20); (1, 10)]
      traverse_2 [40; 30; 20; 10] <- [(1, 40); (1, 30); (1, 20); (1, 10)]
    traverse_1 [1] <- [(1, 40); (1, 30); (1, 20); (1, 10)]
    traverse_2 [40; 30; 20; 10] ->
      traverse_2 [30; 20; 10] ->
        traverse_2 [20; 10] ->
          traverse_2 [10] ->
            traverse_2 [] ->
            traverse_2 [] <- [(1, 40); (1, 30); (1, 20); (1, 10)]
          traverse_2 [10] <- [(2, 10); (1, 40); (1, 30); (1, 20); (1, 10)]
        traverse_2 [20; 10] <- [(2, 20); (2, 10); (1, 40); (1, 30); (1, 20); (1, 10)]
      traverse_2 [30; 20; 10] <- [(2, 30); (2, 20); (2, 10); (1, 40); (1, 30); (1, 20); (1, 10)]
    traverse_2 [40; 30; 20; 10] <- [(2, 40); (2, 30); (2, 20); (2, 10); (1, 40); (1, 30); (1, 20); (1, 10)]
  traverse_1 [2; 1] <- [(2, 40); (2, 30); (2, 20); (2, 10); (1, 40); (1, 30); (1, 20); (1, 10)]
  traverse_2 [40; 30; 20; 10] ->
    traverse_2 [30; 20; 10] ->
      traverse_2 [20; 10] ->
        traverse_2 [10] ->
          traverse_2 [] ->
          traverse_2 [] <- [(2, 40); (2, 30); (2, 20); (2, 10); (1, 40); (1, 30); (1, 20); (1, 10)]
        traverse_2 [10] <- [(3, 10); (2, 40); (2, 30); (2, 20); (2, 10); (1, 40); (1, 30); (1, 20); (1, 10)]
      traverse_2 [20; 10] <- [(3, 20); (3, 10); (2, 40); (2, 30); (2, 20); (2, 10); (1, 40); (1, 30); (1, 20); (1, 10)]
    traverse_2 [30; 20; 10] <- [(3, 30); (3, 20); (3, 10); (2, 40); (2, 30); (2, 20); (2, 10); (1, 40); (1, 30); (1, 20); (1, 10)]
  traverse_2 [40; 30; 20; 10] <- [(3, 40); (3, 30); (3, 20); (3, 10); (2, 40); (2, 30); (2, 20); (2, 10); (1, 40); (1, 30); (1, 20); (1, 10)]
traverse_1 [3; 2; 1] <- [(3, 40); (3, 30); (3, 20); (3, 10); (2, 40); (2, 30); (2, 20); (2, 10); (1, 40); (1, 30); (1, 20); (1, 10)]
- : (int * int) list =
[(3, 40); (3, 30); (3, 20); (3, 10);
 (2, 40); (2, 30); (2, 20); (2, 10);
 (1, 40); (1, 30); (1, 20); (1, 10)]
#

Analysis of each successive call to traverse_2 on the second list, [40; 30; 20; 10]:

• the first call occurs for the last element of the first list, i.e., 1: traverse_2 prepends [(1, 40); (1, 30); (1, 20); (1, 10)] to the empty list;
• the second call occurs for the second to last element of the first list, i.e., 2: traverse_2 prepends [(2, 40); (2, 30); (2, 20); (2, 10)] to the result of the first call;
• the third call occurs for the third to last element of the first list, i.e., 3: traverse_2 prepends [(3, 40); (3, 30); (3, 20); (3, 10)] to the result of the second call.

Computing the Cartesian product of three sets

The Cartesian product of three sets A, B, and C is the set of triples whose first component belongs to A, whose second component belongs to B, and whose third component belongs to C:

A * B * C = {(a, b, c) | (a belongs to A) and (b belongs to B) and (c belongs to C)}

The construction above scales to computing the Cartesian product of three sets:

let test_cartesian_product_3 candidate =
  let b0 = (candidate [] [] [] =
            [])
  and b1 = (candidate [1] [] [] =
            [])
  and b2 = (candidate [] [10] [] =
            [])
  and b3 = (candidate [] [10] [100] =
            [])
  and b4 = (candidate [1] [10] [100] =
            [(1, 10, 100)])
  and b5 = (candidate [1; 2] [10] [100] =
            [(1, 10, 100); (2, 10, 100)])
  and b6 = (candidate [1; 2] [10; 20] [100] =
            [(1, 10, 100); (1, 20, 100);
             (2, 10, 100); (2, 20, 100)])
  and b7 = (candidate [1; 2; 3] [10; 20] [100] =
            [(1, 10, 100); (1, 20, 100);
             (2, 10, 100); (2, 20, 100);
             (3, 10, 100); (3, 20, 100)])
  and b8 = (candidate [1; 2; 3] [10; 20] [100; 200] =
            [(1, 10, 100); (1, 10, 200);
             (1, 20, 100); (1, 20, 200);
             (2, 10, 100); (2, 10, 200);
             (2, 20, 100); (2, 20, 200);
             (3, 10, 100); (3, 10, 200);
             (3, 20, 100); (3, 20, 200)])
  (* etc. *)
  in b0 && b1 && b2 && b3 && b4 && b5 && b6 && b7 && b8 (* etc. *);;

(Again, the indentation in the last three tests is meant to reflect the left-to-right enumeration.)

Given three lists vs_init, ws_init, and xs_init, let us follow their inductive structure to specify three auxiliary functions:

• the first one, traverse_1, is defined over the structure of vs_init, and for each of its elements,
  • the second one, traverse_2, is defined over the structure of ws_init, and for each of its elements,
    • the third one, traverse_3, is defined over the structure of xs_init.

So traverse_3 is defined locally to traverse_2, which is defined locally to traverse_1. To exemplify this nesting, we refer to the inductive specification of traverse_1 as the outer one, to the inductive specification of traverse_2 as the median one, and to the inductive specification of traverse_3 as the inner one. The outer function is specified by induction over a list vs, which is initialized with vs_init, the median one is specified by induction over a list ws, which is initialized with ws_init, and the inner one is specified by induction over a list xs, which is initialized with xs_init:

• outer base case (vs = []):

  the Cartesian product of the empty set, ws_init, and xs_init is the empty set

• outer induction step (vs = v :: vs’):

  assuming that traverse_1 maps vs’ to vs’_and_ws_init_and_xs_init_with_triples_prepended (which is the outer induction hypothesis), let us follow the inductive structure of lists to specify traverse_2:

  • median base case (ws = []):

    there is nothing to prepend, and so the result is vs’_and_ws_init_and_xs_init_with_triples_prepended

  • median induction step (ws = w :: ws’):

    assuming that traverse_2 maps ws’ to vs’_and_ws’_and_xs_init_with_triples_prepended (which is the median induction hypothesis), let us follow the inductive structure of lists to specify traverse_3, whose job is to prepend triples with v as their first component and w as their second component to vs’_ws’_and_xs_init_with_triples_prepended; the third component of these successive triples is each successive element of xs_init:

    • inner base case (xs = []):

      there is nothing to prepend, and so the result is vs’_and_ws’_and_xs_init_with_triples_prepended

    • inner induction step (xs = x :: xs’):

      assuming that traverse_3 maps xs’ to vs’_and_ws’_and_xs’_with_triples_prepended (which is the inner induction hypothesis), it should map x :: xs’ to the list (v, w, x) :: vs’_and_ws’_and_xs’_with_triples_prepended

Remark:

• in the outer induction step, vs’_and_ws_init_and_xs_init_with_triples_prepended is the Cartesian product of vs’, ws_init, and xs_init.

In OCaml:

let cartesian_product_3 vs_init ws_init xs_init =
  let rec traverse_1 vs =
    match vs with
    | [] ->
       []
    | v :: vs' ->
       let vs'_and_ws_init_and_xs_init_with_triples_prepended = traverse_1 vs'
       in let rec traverse_2 ws =
            match ws with
            | [] ->
               vs'_and_ws_init_and_xs_init_with_triples_prepended
            | w :: ws' ->
               let vs'_and_ws'_and_xs_init_with_triples_prepended = traverse_2 ws'
               in let rec traverse_3 xs =
                    match xs with
                    | [] ->
                       vs'_and_ws'_and_xs_init_with_triples_prepended
                    | x :: xs' ->
                       let vs'_and_ws'_and_xs'_with_triples_prepended = traverse_3 xs'
                       in (v, w, x) :: vs'_and_ws'_and_xs'_with_triples_prepended
                  in traverse_3 xs_init
          in traverse_2 ws_init
  in traverse_1 vs_init;;

Analysis:

• cartesian_product_3 is not defined recursively;
• traverse_1 is defined locally to cartesian_product_3;
• traverse_1 is defined recursively, and its recursive call implements the outer induction hypothesis;
• traverse_2 is defined locally to traverse_1;
• traverse_2 is defined recursively, and its recursive call implements the median induction hypothesis.
• traverse_3 is defined locally to traverse_2;
• traverse_3 is defined recursively, and its recursive call implements the inner induction hypothesis.

This OCaml function passes the unit test:

# test_cartesian_product_3 cartesian_product_3;;
- : bool = true
#

The resource file for the present lecture note contains traced versions of traverse_1, traverse_2, and traverse_3 for the zealous reader to visualize the traversals of vs_init, ws_init, and xs_init:

# traced_cartesian_product_3 [1] [10] [100];;
traverse_1 [1] ->
  traverse_1 [] ->
  traverse_1 [] <- []
  traverse_2 [10] ->
    traverse_2 [] ->
    traverse_2 [] <- []
    traverse_3 [100] ->
      traverse_3 [] ->
      traverse_3 [] <- []
    traverse_3 [100] <- [(1, 10, 100)]
  traverse_2 [10] <- [(1, 10, 100)]
traverse_1 [1] <- [(1, 10, 100)]
- : (int * int * int) list = [(1, 10, 100)]
#

Exercise 15

Implement an OCaml function that computes the Cartesian product of four sets, unit-test function and all.

Computing the powerset of a set

The powerset of a set is the set of all its subsets.

Exercise 15

Implement an OCaml function that maps the representation of a set to a representation of its powerset.

A reflective interlude

Alfrothul (eyes on the lecture notes, in the browser): Do you get Exercise 15?

Harald (eyes on the fragments of a solution, in emacs): Not quite, Alfrothul. Not quite. And for quite a while now. These fragments are debris.

Alfrothul: Maybe we should read the interlude that follows the exercise in the lecture notes, sometimes that helps.

Harald: Why not, because I feel really stuck.

Alfrothul: Hey, look, this interlude is a reflective one and it is about us.

Harald: Aren’t they all? Still, in this one, we are working on the same exercise, you perusing the lecture notes with the browser and me editing stuff with emacs.

Alfrothul: And we look just as stuck in there as we feel out here.

Harald: This reflective interlude looks full of itself. Let’s get back to the exercise.

Alfrothul: Wait. How about we keep reading and see what happens next in this interlude. Who knows, maybe what they do there will suggest us how to get unstuck in the exercise, so that we can move on?

Harald (intrigued): Actually, that’s an idea.

Alfrothul: A hopeful one, yes. Man, they are wracking their brains on this exercise. Their fragments are debris.

A towering expert pops in.

The expert: Hi. I am Smith.

Harald (taken by surprise): Agent Smith?

The expert (who saw the movie too): Just call me Brian.

The phone rings. It is an old-style thing plugged to the wall.

Alfrothul: Wait. There was no phone before.

Brian: Actually yes there was. Look at it again.

Alfrothul: OK. I see a phone.

Brian: See? Déjà vu. It’s an induction step. Just get used to it.

Harald: This is getting confusing.

But the phone is still ringing, and so Harald picks it up.

Harald: Huh, hello? Who’s there?

The caller: Hi. Harald here. You’re on speaker.

Harald: Beg pardon?

The caller: I said – Harald here. Oh, wait, that would be Meta-Harald for you.

Brian: See, that’s why I popped in. You guys are not really Harald and Alfrothul, working on an exercise, you are Harald and Alfrothul in an interlude, working on an exercise, and the real Harald and Alfrothul – Meta-Harald and Meta-Alfrothul for you – are stuck on the same exercise and reading this interlude in the hope that what you do there will suggest them how to get unstuck in this exercise so that they can move on.

Alfrothul: Happy to help, but it’s an easy one, as I was just telling Harald – we just need to see what happens next in the interlude we are reading, and we’ll tell Meta-Harald and Meta-Alfrothul once we know. Problem solved.

Harald: And our exercise too. In fact, we are the meta-Harald and the meta-Alfrothul for the Harald and the Alfrothul in the interlude we are reading. I mean, that we are trying to read. Can we get back to it, because something is happening there.

Alfrothul (sententious): Which, by the way, makes our meta-Harald and meta-Alfrothul the meta-meta-Harald and the meta-meta-Alfrothul of the Harald and the Alfrothul in the interlude we are reading, which is fun. And yes, something is happening. They are stuck in the exercise, and they are about to read the interlude that follows the exercise.

Harald: That’s not good. They are supposed to solve the exercise.

Alfrothul: We need to send them an expert.

Brian: At your service.

Alfrothul: Can you go there quick, before they read the interlude?

Brian: And tell them what?

Harald: Whatever, go there quick.

The expert lies down, jacks in, and freezes.

Harald (an eye on the screen): OK, he’s there and introducing himself. And boy does he come as a surprise.

Alfrothul: But what is he going to say? We didn’t tell him.

Harald: Right. Let me call them. (Grabbing the phone.) Meta-Harald? Hold the line please. <click click click click rrrr, click r, click r> Operator? Can you... Oh, you know the drill. OK, thanks.

The connection is made, and Harald waits for his correspondent to pick up.

Harald: Man, they are taking their time. Let me put them on speaker.

Alfrothul: There is a speaker on rotary-dial telephones now?

Harald: Well, this one has one.

Alfrothul: Indeed it does. Hum. Déjà vu. Again. But then...

Vigfus (interrupting): What did the operator say, exactly?

Loki (casually): She mentioned a drill. Droll, isn’t it?

Vigfus: Not that. The other thing she said.

Harald (getting frantic): Harald is about to pick up the phone. Am I talking to myself here? What do I tell them?

Alfrothul (decisive): Introduce yourself and tell them to stop doodling and solve the exercise so that we all can go home.

Brynja: Wait. Why do you want them to solve the exercise? And for that matter, why do Meta-Harald and Meta-Alfrothul want you to solve the exercise?

Loki: If you want someone to blame, I suggest you look into the meta-Harald and meta-Alfrothul of your meta-Harald and meta-Alfrothul, or even, chances are, into their own meta-Harald and meta-Alfrothul. Can’t they solve the exercise themselves?

Alfrothul: Well, let’s not get carried away here. We all want to have a home to go back to.

Loki: Do you? Have you seen your home, Alfrothul?

Alfrothul: Maybe not yet, but I hope I will soon again, the way things are shaping. I don’t need to explain you what’s an induction step, do I?

Bertrand Russell: The logic of this interlude is getting tenuous. Do you guys need a chairperson?

Mimer: Prof. Russell, thanks for stopping by!

Pete Schickele: It’s quite a crowd, Bob.

A voice in the speaker: Huh, hello? Who’s there?

Harald (silencing everyone): Hi. Harald here. You’re on speaker.

The voice: Beg pardon?

Harald: I said – Harald here. Oh, wait, that would be Meta-Harald for you.

Mimer: This is going to take a while.

Halcyon (rolling his eyes): Couldn’t you just explain recursion first?

Vigfus: Guys! Stop everything! The solution of the exercise is just below!

Alfrothul: Told you.

Solution for Exercise 15

The powerset of a set is the set of its subsets. So the powerset of the empty set is a set containing the empty set, and the power set of a singleton set is a set containing both this set and the empty set. As for the powerset of a 2-elements set, it contains 4 subsets: the full set, the empty set, and two singleton sets. And the powerset of a 3-elements set contains 8 subsets. So if a set has size n, the size of its powerset is the power of 2 to the n. Sketching a unit-test function, we can see how the size of the resulting powerset doubles when the size of the given set is incremented by 1:

let test_powerset_int candidate =
  let b0 = (candidate [] =
            [[]])
  and b1 = (candidate [1] =
            [[1]; []])
  and b2 = (candidate [2; 1] =
            [[2; 1]; [2]; [1]; []])
  and b3 = (candidate [3; 2; 1] =
            [[3; 2; 1]; [3; 2]; [3; 1]; [3]; [2; 1]; [2]; [1]; []])
  (* etc. *)
  in b0 && b1 && b2 && b3 (* etc. *);;

The second half of the next powerset is always the previous powerset. As for the first half, it is like the second half, but with a new element prepended to each of its components. Based on this inductive characterization, the code pretty much writes itself:

let powerset_v0 ns_init =
  let rec visit ns =
    match ns with
    | [] ->
       [[]]
    | n :: ns' ->
       let ih = visit ns'
       in List.append (List.map (fun ns -> n :: ns) ih) ih
  in visit ns_init;;

And it passes the unit test too:

# test_powerset_int powerset_v0;;
- : bool = true
#

Aftermath

Vigfus: Oh, no, not again.

Brynja (mildly): Well, this is an aftermath, not an interlude.

Vigfus: OK, make your point. Harald and Alfrothul – especially Alfrothul – are sitting this one out.

Halcyon: Sounds good to me. Do you guys need a chairperson?

Vigfus: By all means. Have a chair.

Halcyon: This armchair will do just fine, thank you.

Brynja: Good. In the definition of powerset_v0 above, the result of List.map is the first argument of List.append. That is silly: List.map allocates a fresh list of results and List.append copies it.

Vigfus: So?

Brynja: So let us fuse this composition of functions into one function where no intermediate list is allocated, something that back in the days, Peter Landin and William Burge called “loop fusion”:

let test_append_map_int candidate =
  let b0 = (candidate succ [0; 1; 2] [10; 20; 30] =
            List.append (List.map succ [0; 1; 2]) [10; 20; 30])
  (* etc. *)
  in b0 (* etc. *);;

Harald: This one is easy to specify inductively. It’s like the map function.

Halcyon: Aren’t you sitting this one out, Harald?

Harald: Oh, right.

Halcyon: Easy does it.

Vigfus: Harald is right, though: append_map is like the map function, except that in the base case, it returns its second argument:

let append_map f vs ws =
  let rec visit vs =
    match vs with
    | [] ->
       ws
    | v :: vs' ->
       f v :: visit vs'
  in visit vs;;

Brynja: Right – append_map is to List.map what List.append is to list_copy.

Vigfus: And it passes the unit test too:

# test_append_map_int append_map;;
- : bool = true
#

Brynja: Yay. This definition satisfies the property that for any function f and for any lists vs and ws, evaluating append_map f vs ws yields the same result as evaluating List.append (List.map f vs) ws.

Harald: Observational equivalence?

Alfrothul (reminded of the midterm project too): Observational equivalence.

Vigfus: You guys are going to wake up Halcyon.

Brynja: And we can now revisit the definition of the powerset function:

let powerset_v1 ns_init =
  let rec visit ns =
    match ns with
    | [] ->
       [[]]
    | n :: ns' ->
       let ih = visit ns'
       in append_map (fun ns -> n :: ns) ih ih
  in visit ns_init;;

Vigfus: Testing, testing:

# test_powerset_int powerset_v1;;
- : bool = true
#

Brynja: And we are done: all the lists allocated by this implementation are part of the result.

Vigfus: Correct me if I’m wrong, but the same property holds for the implementations of the Cartesian product above.

Mimer: This property is known as listlessness, a name due to Phil Wadler, in his PhD thesis at CMU.

Harald: So powerset_v1 is listless, since all the lists it constructs are part of the result.

Alfrothul: And powerset_v0 isn’t, since not all the lists it constructs are part of the result.

Halcyon (stretching): Thank you all for this invigorating aftermath. What’s next?

Brynja: Another exercise...

Halcyon (suspicious): There is no interlude afterwards, is there?

Vigfus: No, no, it’s the end of this lecture note.

Halcyon: That’s a relief, because as I keep telling you, there’s got to be a simpler way to explain self-reference. I mean look at us!

Exercise 16

The goal of this exercise is to study sets of integers whose normalized representation is a sorted list without repetition. To this end, OCaml’s sorting function List.sort comes handy to define the following sorting function over lists of integers:

let sort ns =
 (* sort : int list -> int list *)
  List.sort (fun i j -> if i < j then 0 else 1) ns;;

To wit:

# sort [1; 2];;
- : int list = [1; 2]
# sort [2; 1];;
- : int list = [1; 2]
# sort [3; 1; 2];;
- : int list = [1; 2; 3]
# sort [3; 2; 1];;
- : int list = [1; 2; 3]
#

Exploit this normalized representation to implement set union, set intersection, and set difference. Compare the efficiency of your implementation to the efficiency of the implementations in the solutions for Exercise 4, Exercise 6, and Exercise 9, counting their number of recursive calls.

Subsidiary question: implement a function that adds an element to a given set when this set is represented as a sorted list without repetition.

Mimer: It would be a good idea to consult the Second interlude.

A pragmatic approach to solving Exercise 16

Brynja: Harald and Alfrothul, you have two lists of distinct integers that are sorted in increasing order?

Harald and Alfrothul: Yes ma’am.

Brynja: Let’s construct a list of distinct integers that are sorted in increasing order and whose integers are contained in either of your lists. Harald, is your list empty?

Harald: No, it starts with an integer.

Brynja: Thanks. Alfrothul, is your list empty?

Alfrothul: No, it starts with an integer.

Brynja: Are your integers the same?

Harald and Alfrothul: Yes.

Brynja: OK, let me take it to construct the result. Harald, is the rest of your list empty?

Harald: No, it starts with another integer.

Brynja: Thanks. Alfrothul, is the rest of your list empty?

Alfrothul: No, it starts with an integer.

Brynja: Thanks. Are your integers the same?

Harald and Alfrothul: No.

Brynja: Which integer is the smallest?

Harald: Mine.

Brynja: OK, let me take it to construct the result. Harald, is the rest of the rest of your list empty?

Harald: No, it starts with another integer.

Brynja: Thanks. Is this integer the same as Alfrothul’s current integer?

Harald and Alfrothul: No.

Brynja: Which integer is the smallest?

Alfrothul: Mine.

Brynja: OK, let me take it to construct the result. Alfrothul, is the rest of the rest of your list empty?

Alfrothul: Yes.

Brynja: Thanks. Let me take Harald’s integer and the rest of his list to construct the result.

Harald: This is neat. You constructed the result by traversing each of our lists in parallel.

Alfrothul: And by traversing them only once.

Brynja: Well, what else? Your lists are already sorted.

Harald: But what if they are not? Shouldn’t we check first?

Brynja: No need – you could check as you go.

Alfrothul: You mean as we traverse them. Neat. This way, we would still traverse them only once.

Mimer: The art of Computer Science is to exploit the structure of the data at hand to design and implement minimalistic algorithms.

Halcyon: How about we construct a list of distinct integers that are sorted in increasing order and whose integers are contained in both of Harald and Alfrothul’s lists?

Vigfus: Great idea.

After hours

Alfrothul: In light of recent events...

Harald: ...our definition of set_add_sorted is, ah, over-engineered.

Alfrothul: Maybe we should start by writing its unit-test function.

Harald: Ah, right, we also need to do that.

Alfrothul: No, I mean – start. As in: do it first.

Harald: The one in the resource file is not good enough?

Alfrothul: There isn’t one, Harald.

Harald: Harumph.

Alfrothul: Let’s pick a simple set, and then review the possibilities.

Harald: Shoot.

Alfrothul: How about [2; 4] for the set, and then for elements to add to this set, well, 1, 2, 3, 4, and 5. They cover all the possibilities: the element is smaller or larger than all the elements in the set, the element already belongs to the set, and the element fits in the middle.

Harald: Let me run point:

let silent = true;;

Alfrothul: Now what.

Harald: Well, we might as well do it right:

let test_set_add_sorted candidate =
  let b0 = (let e = 0
            and es = []
            in let actual_result = candidate e es
               and expected_result = [0]
               in if actual_result = expected_result
                  then true
                  else if silent
                  then false
                  else let () = Printf.printf
                                  "test_set_add_sorted failed in b0 with %s as element and %s as set with result %s instead of %s\n"
                                  (show_int e) (show_list show_int es) (show_list show_int actual_result) (show_list show_int expected_result)
                       in false)
  in b0;;

Alfrothul: Wow. That is thorough.

Harald: Right. And quite a mouthful too.

Alfrothul: Should we factor it?

Harald: Factor it.

Alfrothul: You know, into a function:

let test_set_add_sorted_one candidate test given_element given_set expected_result =
  let actual_result = candidate given_element given_set
  in if actual_result = expected_result
     then true
     else if silent
     then false
     else let () = Printf.printf
                     "test_set_add_sorted failed in %s with %s as element and %s as set with result %s instead of %s\n"
                     test (show_int given_element) (show_list show_int given_set) (show_list show_int actual_result) (show_list show_int expected_result)
          in false;;

Harald: Ah, right:

let test_set_add_sorted_v1 candidate =
  let b0 = test_set_add_sorted_one_v0 candidate "b0" 0 [] [0]
  in b0;;

Alfrothul: Actually, if we test several functions, it would be nice to have their name too in the error message.

Harald: Then we would need to parameterize the unit-test function with this name too:

let test_set_add_sorted name candidate =
  let b0 = test_set_add_sorted_one name candidate "b0" 0 [] [0]
  in b0;;

Alfrothul: Thanks:

let test_set_add_sorted_one name candidate test given_element given_set expected_result =
  let actual_result = candidate given_element given_set
  in if actual_result = expected_result
     then true
     else if silent
     then false
     else let () = Printf.printf
                     "test_set_add_sorted failed for %s in %s with %s as element and %s as set with result %s instead of %s\n"
                     name test (show_int given_element) (show_list show_int given_set) (show_list show_int actual_result) (show_list show_int expected_result)
          in false;;

Harald: I think we’re good to go here.

Alfrothul: Right. So, adding 1 to [2; 4] is simple: 1 is smaller than the first element of the given list, 2, and therefore it should occur first in the resulting list. So:

let test_set_add_sorted name candidate =
  let b0 = test_set_add_sorted_one name candidate "b0" 0 [] [0]
  and b1 = test_set_add_sorted_one name candidate "b1" 1 [2; 4] [1; 2; 4]
  in b0;;

Harald: Right – you supply test_set_add_sorted_one with the name of the candidate function, the candidate function, the element to add, the set to be added to, the expected result, and the name of the clause in the test.

Alfrothul: That’s concise, but we didn’t test test_set_add_sorted_one.

Harald: Presto:

# test_set_add_sorted_one "foo" (fun e es -> e :: es) "bar 1 [2; 4] [1; 2; 4];;
- : bool = true
#

Alfrothul: OK. A negative test now:

# test_set_add_sorted_one "foo" (fun e es -> e :: es) "bar 0 [2; 4] [1; 2; 4];;
- : bool = false
#

Alfrothul: No error message?

Harald: That’s because of the silent flag. <clickety clickety click> Try again:

# test_set_add_sorted_one "foo" (fun e es -> e :: es) "bar" 0 [2; 4] [1; 2; 4];;
test_set_add_sorted failed for foo in bar with 0 as element and [2; 4] as set with result [0; 2; 4] instead of [1; 2; 4]
- : bool = false
#

Alfrothul: That looks right.

Vigfus: Why is the error message about test_set_add_sorted? It is only emitted when test_set_add_sorted_one is called.

Harald: Well, test_set_add_sorted_one is an auxiliary function. We only use test_set_add_sorted, so it makes sense to only see that name in the error message.

Vigfus: That makes sense. Thanks.

Alfrothul: Moving on – adding 2 to [2; 4] is also simple: 2 already occurs in [2; 4] and therefore there is nothing to add to this list:

let test_set_add_sorted name candidate =
  let b0 = test_set_add_sorted_one name candidate "b0" 0 [] [0]
  and b1 = test_set_add_sorted_one name candidate "b1" 1 [2; 4] [1; 2; 4]
  and b2 = test_set_add_sorted_one name candidate "b2" 2 [2; 4] [2; 4]
  in b0 && b1 && b2;;

Harald: To add 3 to [2; 4], we simply insert it between 2 and 4:

let test_set_add_sorted name candidate =
  let b0 = test_set_add_sorted_one name candidate "b0" 0 [] [0]
  and b1 = test_set_add_sorted_one name candidate "b1" 1 [2; 4] [1; 2; 4]
  and b2 = test_set_add_sorted_one name candidate "b2" 2 [2; 4] [2; 4]
  and b3 = test_set_add_sorted_one name candidate "b3" 3 [2; 4] [2; 3; 4]
  in b0 && b1 && b2 && b3;;

Alfrothul: And to add 4 to [2; 4], we simply return [2; 4] since 4 already occurs in this list:

let test_set_add_sorted name candidate =
  let b0 = test_set_add_sorted_one name candidate "b0" 0 [] [0]
  and b1 = test_set_add_sorted_one name candidate "b1" 1 [2; 4] [1; 2; 4]
  and b2 = test_set_add_sorted_one name candidate "b2" 2 [2; 4] [2; 4]
  and b3 = test_set_add_sorted_one name candidate "b3" 3 [2; 4] [2; 3; 4]
  and b4 = test_set_add_sorted_one name candidate "b4" 4 [2; 4] [2; 4]
  in b0 && b1 && b2 && b3 & b4;;

Harald: And to add 5 to [2; 4], we simply insert it after 2 and 4:

let test_set_add_sorted name candidate =
  let b0 = test_set_add_sorted_one name candidate "b0" 0 [] [0]
  and b1 = test_set_add_sorted_one name candidate "b1" 1 [2; 4] [1; 2; 4]
  and b2 = test_set_add_sorted_one name candidate "b2" 2 [2; 4] [2; 4]
  and b3 = test_set_add_sorted_one name candidate "b3" 3 [2; 4] [2; 3; 4]
  and b4 = test_set_add_sorted_one name candidate "b4" 4 [2; 4] [2; 4]
  and b5 = test_set_add_sorted_one name candidate "b5" 5 [2; 4] [2; 4; 5]
  in b0 && b1 && b2 && b3 && b4 && b5;;

Alfrothul: And there we are.

Harald: Right. And our initial definition of set_add_sorted was indeed over-engineered.

If you have a procedure with ten parameters,

you probably missed some.

—Alan Perlis‘s programming epigram #11

Resources

• The OCaml code for the present lecture note (latest version: 20 Mar 2020).

Version

Added the after-hours part [20 Mar 2020]

Added the pragmatic approach to solving Exercise 16 [17 Mar 2020]

Attuned the statement of completeness_of_set_minus, thanks to Jia Tang’s eagle eye [16 Mar 2020]

Fixed the access to the resource file, thanks to Ayrton San Joaquin’s eagle eye [15 Mar 2020]

Created [14 Mar 2020]