The samefringe problem¶
The following problem is a classic: given two binary trees, check whether traversing them depth-first and from left to right gives the same “fringe”, i.e., the same series of values:
type 'a binary_tree =
| Leaf of 'a
| Node of 'a binary_tree * 'a binary_tree;;
The challenge is that the two trees are not shaped in the same way, and therefore they cannot be traversed synchronously.
Resources¶
- The OCaml code for the present lecture note (latest version: 14 Apr 2019).
The samefringe problem: the unit tests¶
The following unit-test function collects a sample of telling examples:
let test_samefringe_int candidate =
let b0 = (candidate (Leaf 1)
(Leaf 1)
= true) (* common fringe: 1 *)
and b1 = (candidate (Leaf 1)
(Leaf 2)
= false)
and b2 = (candidate (Leaf 1)
(Node (Leaf 1,
Leaf 2))
= false)
and b3 = (candidate (Node (Leaf 1,
Leaf 2))
(Node (Leaf 1,
Leaf 2))
= true) (* common fringe: 1, 2 *)
and b4 = (candidate (Node (Node (Leaf 1,
Leaf 2),
Leaf 3))
(Node (Leaf 1,
Node (Leaf 2,
Leaf 3)))
= true) (* common fringe: [1; 2; 3] *)
and b5 = (candidate (Node (Node (Node (Leaf 1,
Leaf 2),
Leaf 3),
Leaf 4))
(Node (Leaf 1,
Node (Leaf 2,
Node (Leaf 3,
Leaf 4))))
= true) (* common fringe: 1, 2, 3, 4 *)
and b6 = (candidate (Node (Node (Node (Leaf 1,
Leaf 2),
Leaf 3),
Leaf 4))
(Node (Leaf 1,
Node (Leaf 2,
Node (Leaf 3,
Node (Leaf 4,
Leaf 5)))))
= false)
and b7 = (candidate (Node (Node (Node (Node (Leaf 0,
Leaf 1),
Leaf 2),
Leaf 3),
Leaf 4))
(Node (Leaf 1,
Node (Leaf 2,
Node (Leaf 3,
Node (Leaf 4,
Leaf 5)))))
= false)
(* etc. *)
in b0 && b1 && b2 && b3 && b4 && b5 && b6 && b7;;
In these telling examples,
- the common fringe is a sequence of positive integers, and
- fringes mismatch because a mismatching integer or because one fringe is shorter than the other.
Fringe-preserving transformations¶
To automate the unit tests, one can generate a random binary tree, but how can one manufacture another tree with the same fringe but with a different structure? The answer is: by rotating its inner nodes, as depicted below.
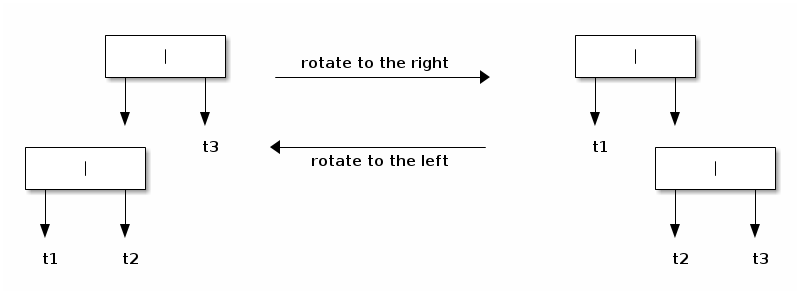
So given a binary tree, we can traverse it and given any three adjacent subtrees, either generate the left configuration or the right one:
let rotate_randomly_3 t1 t2 t3 =
(* 'a binary_tree -> 'a binary_tree -> 'a binary_tree -> 'a binary_tree *)
if Random.bool ()
then Node (t1, Node (t2, t3))
else Node (Node (t1, t2), t3);;
Now how do we program this random tree rotator? At first it seems that structural recursion falls short, since all that the induction step provides is access to the two subtrees of a node, not to their structure.
It is tempting to flout structural recursion and peek inside each node to analyze the structure of its subtrees:
let rotate_binary_tree_randomly_v0 t
(* rotate_binary_tree_randomly_v0 : 'a binary_tree -> 'a binary_tree *)
= let rec visit t =
match t with
| Leaf v ->
...
| Node (t1, t2) ->
(match t1 with
| Leaf v1 ->
(match t2 with
| Leaf v2 ->
...
| Node (t21, t22) ->
...
| Node (t11, t12) ->
(match t2 with
| Leaf v2 ->
...
| Node (t21, t22) ->
...
in visit t;;
Analysis:
t = Leaf v
there is nothing to rotate, so the result should be t itself
t = Node (Leaf v1, Leaf v2)
there is nothing to rotate, so the result should be t itself
t = Node (Leaf v1, Node (t21, t22))
there are 3 subtrees to rotate: Leaf v1, the result of rotating t21, and the result of rotating t22
t = Node (Node (t11, t12), Leaf v2)
there are 3 subtrees to rotate: the result of rotating t11, the result of rotating t12, and Leaf v2
t = Node (Node (t11, t12), Node (t21, t22))
there are 4 subtrees to rotate:
- we can either leave the first in place and rotate the 3 others,
- or rotate the 3 first, and leave the last in place.
All in all:
let rotate_randomly_4 t1 t2 t3 t4 =
(* rotate_randomly_4 : 'a binary_tree -> 'a binary_tree -> 'a binary_tree -> 'a binary_tree -> 'a binary_tree * 'a binary_tree *)
if Random.bool ()
then (t1, rotate_randomly_3 t2 t3 t4)
else (rotate_randomly_3 t1 t2 t3, t4);;
let rotate_binary_tree_randomly_v0 t
(* rotate_binary_tree_randomly_v0 : 'a binary_tree -> 'a binary_tree *)
= let rec visit t =
match t with
| Leaf v ->
Leaf v
| Node (t1, t2) ->
(match t1 with
| Leaf v1 ->
(match t2 with
| Leaf v2 ->
Node (Leaf v1, Leaf v2)
| Node (t21, t22) ->
rotate_randomly_3 (Leaf v1) (visit t21) (visit t22))
| Node (t11, t12) ->
(match t2 with
| Leaf v2 ->
rotate_randomly_3 (visit t11) (visit t12) (Leaf v2)
| Node (t21, t22) ->
let (t1', t2') = rotate_randomly_4 (visit t11) (visit t12) (visit t21) (visit t22)
in Node (t1', t2')))
in visit t;;
But do we need to flout structural recursion? Of course not. We can take stock on the fact that the result of visit will be either one binary tree or two (which is the induction hypothesis). Then, in the induction step, we can analyze each induction hypothesis, and then rotate accordingly:
type 'a one_or_two =
| One of 'a
| Two of 'a * 'a;;
let rotate_binary_tree_randomly_v1 t
= let rec visit t =
match t with
| Leaf v ->
One (Leaf v)
| Node (t1, t2) ->
(match visit t1 with
| One t1' ->
(match visit t2 with
| One t2' ->
Two (t1', t2')
| Two (t21', t22') ->
One (rotate_randomly_3 t1' t21' t22'))
| Two (t11', t12') ->
(match visit t2 with
| One t2' ->
One (rotate_randomly_3 t11' t12' t2')
| Two (t21', t22') ->
let (t1'', t2'') = rotate_randomly_4 t11' t12' t21' t22'
in Two (t1'', t2'')))
in match visit t with
| One t' ->
t'
| Two (t1', t2') ->
Node (t1', t2');;
Analysis:
base case: t = Leaf v
the result is one binary tree, i.e., One (Leaf v)
induction step: t = Node (t1, t2)
if the induction hypothesis on t1 is one binary tree, i.e., One t1', then
if the induction hypothesis on t2 is one binary tree, i.e., One t2', then
the result is two binary trees, i.e., Two (t1', t2')
if the induction hypothesis on t2 is two binary trees, i.e., Two (t21', t22'), then
the result is the binary tree obtained by rotating t1', t21', and t22'
if the induction hypothesis on t1 is two binary trees, i.e., Two (t11', t12'), then
if the induction hypothesis on t2 is one binary tree, i.e., One t2', then
the result is the binary tree obtained by rotating t11', t12', and t2'
if the induction hypothesis on t2 is two binary trees, i.e., Two (t21', t22'), then
the result is two binary trees, i.e., either the result of rotating t11', t12', t21', and t22'
And then we can express rotate_binary_tree_randomly_v1 using fold_binary_tree:
let rotate_binary_tree_randomly_v2 t
= match fold_binary_tree (fun v -> One (Leaf v))
(fun ih1 ih2 ->
(match ih1 with
| One t1' ->
(match ih2 with
| One t2' ->
Two (t1', t2')
| Two (t21', t22') ->
One (rotate_randomly_3 t1' t21' t22'))
| Two (t11', t12') ->
(match ih2 with
| One t2' ->
One (rotate_randomly_3 t11' t12' t2')
| Two (t21', t22') ->
let (t1'', t2'') = rotate_randomly_4 t11' t12' t21' t22'
in Two (t1'', t2''))))
t with
| One t' ->
t'
| Two (t1', t2') ->
Node (t1', t2');;
The samefringe problem: the unit tests, revisited¶
We are now in position to flesh out the unit-test function with random binary trees by parameterizing the unit-test function with a random binary-tree rotator to generate a second binary tree with the same fringe out of a random binary tree:
let test_samefringe_int rotate_binary_tree_randomly candidate =
let b0 = (candidate (Leaf 1)
(Leaf 1)
= true)
...
and b8 = (let t1 = generate_random_binary_tree_int 7
in let t2 = rotate_binary_tree_randomly t1
in if candidate t1 t2 = true
then if candidate t2 t1 = true
then true
else let () = Printf.printf "The samefringe test failed on\n%s\nand\n%s\n"
(show_binary_tree show_int t2)
(show_binary_tree show_int t1)
in false
else let () = Printf.printf "The samefringe test failed on\n%s\nand\n%s\n"
(show_binary_tree show_int t1)
(show_binary_tree show_int t2)
in false)
(* etc. *)
in b0 && b1 && b2 && b3 && b4 && b5 && b6 && b7 && b8;;
Analysis:
- t1 denotes a random binary tree of integers whose depth is at most 7,
- t2 denotes a randomly rotated version of the tree denoted by t1,
- we verify that the first tree and the second tree have the same fringe, and if they do not, we issue an error message, and
- we verify that the second tree and the first tree have the same fringe, and if they do not, we issue the converse error message.
The fringe of a tree as a list¶
The simplest way to represent the fringe of a binary tree is to list the elements occurring in its leaves when the tree is traversed depth-first and from left to right, i.e., in the order these elements are both read and printed out.
So for example, in the unit-test function above,
- the fringe of Leaf 1 is [1],
- the fringe of Leaf 2 is [2],
- the fringe of Node (Leaf 1, Leaf 2) is [1; 2],
- the fringe of Node (Node (Leaf 1, Leaf 2), Leaf 3) is [1; 2; 3],
- the fringe of Node (Leaf 1, Node (Leaf 2, Leaf 3)) is [1; 2; 3],
- the fringe of Node (Node (Node (Leaf 1, Leaf 2), Leaf 3), Leaf 4) is [1; 2; 3; 4],
- the fringe of Node (Leaf 1, Node (Leaf 2, Node (Leaf 3, Leaf 4))) is [1; 2; 3; 4], and
- the fringe of Node (Leaf 1, Node (Leaf 2, Node (Leaf 3, Node (Leaf 4, Leaf 5)))) is [1; 2; 3; 4; 5].
Let us write a fringe function that maps a binary tree to its fringe.
Intuitively, the corresponding unit-test function is simple to write – for any given binary tree, omit all the constructors and collect the leaf elements in a list, in the same order:
let test_makefringe_int candidate =
(* test_makefringe_int : (int binary_tree -> int list) -> bool *)
let b0 = (candidate (Leaf 0)
= [0])
and b1 = (candidate (Node (Leaf 1, Leaf 2))
= [1; 2])
and b2 = (candidate (Node (Leaf 1, Node (Leaf 2, Leaf 3)))
= [1; 2; 3])
and b3 = (candidate (Node (Node (Leaf 1, Leaf 2), Leaf 3))
= [1; 2; 3])
and b4 = (candidate (Node (Node (Leaf 1, Leaf 2), Node (Leaf 3, Leaf 4)))
= [1; 2; 3; 4])
(* etc. *)
in b0 && b1 && b2 && b3 && b4;;
Formally, the function is specified by induction, following the structure of binary trees:
base case: t = Leaf v
given any value v (noting its syntactic representation as v), the fringe of Leaf v is the singleton list containing v
induction step: t = Node (t1, t2)
given any binary tree t1 whose fringe is v1s (which is the first induction hypothesis) and given any binary tree t2 whose fringe is v2s (which is the second induction hypothesis), the fringe of Node (t1, t2) is the result of concatenating v1s and v2s
In OCaml, the makefringe function is implemented as a structurally recursive function mapping a (deep) binary tree of values to a (flat) list of these values:
let makefringe_v0 t_init =
(* makefringe_v0 : 'a binary_tree -> 'a list *)
let rec flatten t =
match t with
| Leaf v ->
[v]
| Node (t1, t2) ->
flatten t1 @ flatten t2
in flatten t_init;;
This OCaml function passes the unit test:
# test_makefringe_int makefringe_v0;;
- : bool = true
#
The fringe of a tree as a list, revisited¶
As usual, it is not a very good idea to use list concatenation in a recursive function because of its linear time and space overhead. Better use an accumulator:
base case: t = Leaf v
given any value v (noting its syntactic representation as v) and any accumulator a (denoted by a), the fringe of Leaf v is the list obtained by cons’ing v on top of a
induction step: t = Node (t1, t2)
the (first) induction hypothesis on the tree denoted by t1 is a function that, given an accumulator a, prepends the leaves of this tree to a
the (second) induction hypothesis on the tree denoted by t2 is a function that, given an accumulator a, prepends the leaves of this tree to a
given any accumulator a, applying the second induction hypothesis to this accumulator yields a new accumulator, and applying the first induction hypothesis to this accumulator yields a list where the leaves of the tree denoted by Node (t1, t2) are prepended to the given accumulator
In OCaml, the makefringe function is implemented as a structurally recursive function mapping a (deep) binary tree of values to a (flat) list of these values:
let makefringe_v1 t_init =
let rec flatten t a =
match t with
| Leaf n ->
n :: a
| Node (t1, t2) ->
flatten t1 (flatten t2 a)
in flatten t_init [];;
This function is listless since it only uses :: to construct the result. And it passes the unit test too:
# test_makefringe_int makefringe_v1;;
- : bool = true
#
The samefringe problem, Take 0: easy does it¶
In the following straightforward solution to the samefringe problem, the fringes of the two given trees are tested for equality:
let samefringe_v1 t1 t2 =
(* samefringe_v1 : 'a binary_tree -> 'a binary_tree -> bool *)
makefringe_v1 t1 = makefringe_v1 t2;;
This OCaml function passes the unit test:
# test_samefringe_int rotate_binary_tree_randomly_v1 samefringe_v1;;
- : bool = true
#
That was quick. What is less quick is the flattening of large trees, but that is seemingly unavoidable: a computer’s gotta do what a computer’s gotta do. Two annoying cases, however, stand out:
What if one of the two lists is shorter than the other?
Then it was useless to construct the rest of the longer list.
What if the two lists differ in one of their first elements?
Then it was useless to construct the rest of both lists.
These cases come across more clearly if we program the fringe comparison ourselves rather than relying on OCaml’s equality predicate:
let samefringe_v2 t1 t2 =
(* samefringe_v2 : 'a binary_tree -> 'a binary_tree -> bool *)
let rec loop n1s n2s =
match n1s with
| [] ->
(match n2s with
| [] ->
true
| n2 :: n2s' ->
false)
| n1 :: n1s' ->
(match n2s with
| [] ->
false
| n2 :: n2s' ->
n1 = n2 && loop n1s' n2s')
in loop (makefringe_v1 t1) (makefringe_v1 t2);;
To wit:
# test_samefringe_int rotate_binary_tree_randomly_v1 samefringe_v2;;
- : bool = true
#
So overall, constructing the two lists to represent the fringes is an overkill both in space and in time. Its cost is proportional to the total number of leaves in the given trees, and it is unwarranted if these two trees do not have the same fringe.
The samefringe problem, Take 1: minimizing space¶
In retrospect, there is no need to construct the fringe. Instead, we could just index each tree depth first and from left to right (using nth_depth_first_left_to_right as defined in the accompanying file), and progressively increase the index until one of both trees run out of leaves to index:
- at the end of this process, if both trees run out of leaves, they have the same fringe;
- at the end of this process, if one tree runs out of leaves but not the other, one is smaller than the other, and their fringes differ;
- in the course of this process, if both trees do not have the same leaf at the same index, they do not have the same fringe; and
- in the course of this process, if both trees have the same leaf at the same index, then the process can continue at the next index.
So overall, we say good bye to the blanket equality test from Version 1, and we incrementalize it to test each pair of leaves for each successive index:
let samefringe_v3 t1 t2 =
(* samefringe_v3 : 'a binary_tree -> 'a binary_tree -> bool *)
let rec enumerate i =
match nth_depth_first_left_to_right t1 i with
| Some v1 ->
(match nth_depth_first_left_to_right t2 i with
| Some v2 ->
if v1 = v2
then enumerate (succ i)
else false
| None ->
false)
| None ->
(match nth_depth_first_left_to_right t2 i with
| Some v2 ->
false
| None ->
true)
in enumerate 0;;
This OCaml function passes the unit test:
# test_samefringe_int rotate_binary_tree_randomly_v1 samefringe_v3;;
- : bool = true
#
That was simple, and it was space optimal too: no intermediate list has been created.
Time-wise, this solution is not optimal: each tree is repeatedly traversed in a way that fits the sum 1 + 2 + 3 + ..., i.e., quadratically.
The samefringe problem, Take 2: trading time for space¶
The middle ground is to amortize both time and space by representing the fringe as a lazy list:
type 'a lazy_list =
| Nil
| Cons of 'a * 'a lazy_list Lazy.t;;
let makefringe_v2 t =
(* makefringe_v2 : 'a binary_tree -> 'a lazy_list *)
let rec flatten t a =
match t with
| Leaf n ->
Cons (n, a)
| Node (t1, t2) ->
flatten t1 (lazy (flatten t2 a))
in flatten t (lazy Nil);;
let samefringe_v4 t1 t2 =
let rec loop n1s n2s =
match n1s with
| Nil ->
(match n2s with
| Nil ->
true
| Cons (n2, n2s') ->
false)
| Cons (n1, n1s') ->
(match n2s with
| Nil ->
false
| Cons (n2, n2s') ->
n1 = n2 && loop (Lazy.force n1s') (Lazy.force n2s'))
in loop (makefringe_v2 t1) (makefringe_v2 t2);;
Rationale:
- the fringe is constructed on demand, and
- only if the two given trees have the same fringe, it is constructed in toto.
This OCaml function passes the unit test:
# test_samefringe_int rotate_binary_tree_randomly_v1 samefringe_v4;;
- : bool = true
#
Concretely, the two given trees are only traversed as long as the prefixes of their fringes are the same.
The accompanying file contains traced versions of samefringe_v4 and makefringe_v2:
- samefringe_v4 emits a trace for its initial call and for its final return as well as for each tail call to loop; and
- makefringe_v2 emits a trace for its initial call as well as an indented trace for each call to flatten. This indentation reflects the depth of the current subtree that is being flattened.
As such, these traced versions illustrate the asynchronous traversals of the two binary trees as they are incrementally flattened, interrupted as these traversals are by the next tail call to loop.
Let us illustrate the samefringe problem for the following two trees:
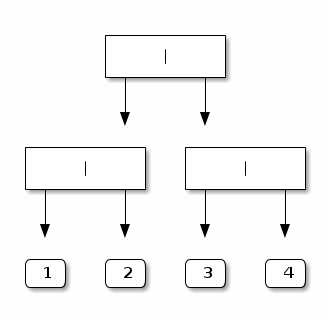
The first one is bushy:
Node (Node (Leaf 1, Leaf 2), Node (Leaf 3, Leaf 4))Pictorially:
Flattening this bushy tree with the traced version of makefringe_v0 found in the accompanying file that goes depth first and from left to right gives rise to the following trace:
# traced_makefringe_v0 show_int (Node (Node (Leaf 1, Leaf 2), Node (Leaf 3, Leaf 4)));; makefringe_v0 (Node (Node (Leaf 1, Leaf 2), Node (Leaf 3, Leaf 4))) -> flatten (Node (Node (Leaf 1, Leaf 2), Node (Leaf 3, Leaf 4))) ... -> flatten (Node (Leaf 1, Leaf 2)) ... -> flatten (Leaf 1) ... -> flatten (Leaf 2) ... -> flatten (Node (Leaf 3, Leaf 4)) ... -> flatten (Leaf 3) ... -> flatten (Leaf 4) ... -> - : int list = [1; 2; 3; 4] #Each indentation accounts for the nesting of each subtree and the corresponding calls to flatten.
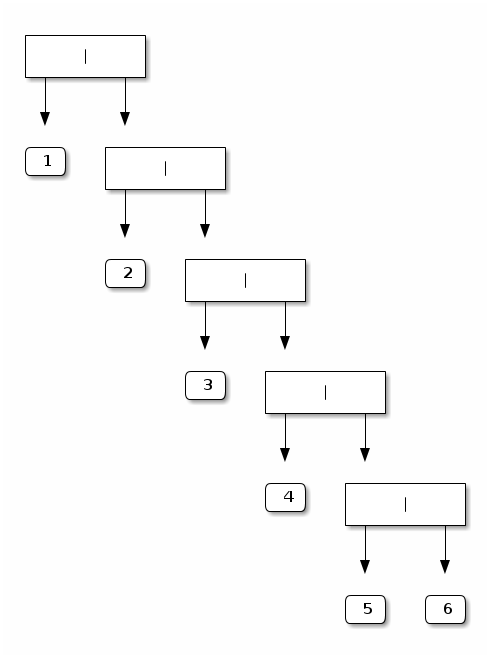
The second tree is elongated:
Node (Leaf 1, Node (Leaf 2, Node (Leaf 3, Node (Leaf 4, Node (Leaf 5, Leaf 6)))))Pictorially:
Flattening this bushy tree with the traced version of makefringe_v0 that goes depth first and from left to right gives rise to the following trace:
# traced_makefringe_v0 show_int (Node (Leaf 1, (Node (Leaf 2, Node (Leaf 3, Node (Leaf 4, Node (Leaf 5, Leaf 6)))))));; makefringe_v0 (Node (Leaf 1, Node (Leaf 2, Node (Leaf 3, Node (Leaf 4, Node (Leaf 5, Leaf 6)))))) -> flatten (Node (Leaf 1, Node (Leaf 2, Node (Leaf 3, Node (Leaf 4, Node (Leaf 5, Leaf 6)))))) ... -> flatten (Leaf 1) ... -> flatten (Node (Leaf 2, Node (Leaf 3, Node (Leaf 4, Node (Leaf 5, Leaf 6))))) ... -> flatten (Leaf 2) ... -> flatten (Node (Leaf 3, Node (Leaf 4, Node (Leaf 5, Leaf 6)))) ... -> flatten (Leaf 3) ... -> flatten (Node (Leaf 4, Node (Leaf 5, Leaf 6))) ... -> flatten (Leaf 4) ... -> flatten (Node (Leaf 5, Leaf 6)) ... -> flatten (Leaf 5) ... -> flatten (Leaf 6) ... -> - : int list = [1; 2; 3; 4; 5; 6] #
The following interaction illustrates the asynchronous traversals:
- initially, makefringe_v2 is called on each of the two given trees, and starts flattening them, finding the first leave in two (indented) calls for the second tree, and in three (indented) calls for the first tree;
- loop checks that the two lazy lists start with the same integer
(namely 1), which they do, and resumes the two flattenings with the
same indentation, as if each traversal had not been interrupted:
- the second leaf is found in two calls for the second tree, and
- the second leaf is found in one call for the first tree;
- loop checks that the two lazy lists start with the same integer
(namely 2), which they do, and resumes the two flattenings, again
with an indentation consistent with each traversal:
- the third leaf is found in two calls for the second tree, and
- the third leaf is found after one return and two calls for the first tree;
- loop checks that the two lazy lists start with the same integer
(namely 3), which they do, and resumes the two flattenings, still
with an indentation consistent with each traversal:
- the fourth leaf is found in two calls for the second tree, and
- the third leaf is found in one call for the first tree;
- loop checks that the two lazy lists start with the same integer
(namely 4), which they do, and resumes the two flattenings, still
with an indentation consistent with each traversal:
- the fifth leaf is found in two calls for the second tree, and
- the first tree is exhausted;
- the computation is complete and the result is false since the fringes of the two trees differ.
All in all, when applying traced_makefringe_v2, the traced calls to flatten are interleaved fragments of the traced calls to flatten when applying traced_makefringe_v0, from each node to its leftmost leaf:
# traced_samefringe_v4 show_int (Node (Node (Leaf 1, Leaf 2), Node (Leaf 3, Leaf 4))) (Node (Leaf 1, (Node (Leaf 2, Node (Leaf 3, Node (Leaf 4, Node (Leaf 5, Leaf 6)))))));;
samefringe_v4 (Node (Node (Leaf 1, Leaf 2), Node (Leaf 3, Leaf 4)))
(Node (Leaf 1, Node (Leaf 2, Node (Leaf 3, Node (Leaf 4, Node (Leaf 5, Leaf 6)))))) ->
makefringe_v2 (Node (Leaf 1, Node (Leaf 2, Node (Leaf 3, Node (Leaf 4, Node (Leaf 5, Leaf 6)))))) ->
flatten (Node (Leaf 1, Node (Leaf 2, Node (Leaf 3, Node (Leaf 4, Node (Leaf 5, Leaf 6)))))) ... ->
flatten (Leaf 1) ... ->
makefringe_v2 (Node (Node (Leaf 1, Leaf 2), Node (Leaf 3, Leaf 4))) ->
flatten (Node (Node (Leaf 1, Leaf 2), Node (Leaf 3, Leaf 4))) ... ->
flatten (Node (Leaf 1, Leaf 2)) ... ->
flatten (Leaf 1) ... ->
loop (Cons (1, ...)) (Cons (1, ...)) ->
flatten (Node (Leaf 2, Node (Leaf 3, Node (Leaf 4, Node (Leaf 5, Leaf 6))))) ... ->
flatten (Leaf 2) ... ->
flatten (Leaf 2) ... ->
loop (Cons (2, ...)) (Cons (2, ...)) ->
flatten (Node (Leaf 3, Node (Leaf 4, Node (Leaf 5, Leaf 6)))) ... ->
flatten (Leaf 3) ... ->
flatten (Node (Leaf 3, Leaf 4)) ... ->
flatten (Leaf 3) ... ->
loop (Cons (3, ...)) (Cons (3, ...)) ->
flatten (Node (Leaf 4, Node (Leaf 5, Leaf 6))) ... ->
flatten (Leaf 4) ... ->
flatten (Leaf 4) ... ->
loop (Cons (4, ...)) (Cons (4, ...)) ->
flatten (Node (Leaf 5, Leaf 6)) ... ->
flatten (Leaf 5) ... ->
loop (Nil) (Cons (5, ...)) ->
samefringe_v4
Node (Node (Leaf 1, Leaf 2), Node (Leaf 3, Leaf 4))
Node (Leaf 1, Node (Leaf 2, Node (Leaf 3, Node (Leaf 4, Node (Leaf 5, Leaf 6)))))
<- false
- : bool = false
#
The samefringe problem, Take 3: constructing only one fringe¶
Alternatively, we could only construct one fringe for one of the given trees, and then recursively traverse the other, incrementally peeling off this fringe:
let samefringe_v5 t1 t2 =
(* samefringe_v5 : 'a binary_tree -> 'a binary_tree -> bool *)
let rec visit t1 n2s =
(* visit : 'a binary_tree -> 'a list -> 'a list option *)
match t1 with
| Leaf n1 ->
(match n2s with
| [] ->
...
| n2 :: n2s' ->
...)
| Node (t11, t12) ->
(match visit t11 n2s with
| None ->
...
| Some n2s' ->
...)
in match visit t1 (makefringe_v1 t2) with
| None ->
false
| Some [] ->
true
| Some (_ :: _) ->
false;;
Exercise 24¶
- Complete the definition of samefringe_v5.
- Modify this definition (i.e., implement a new function samefringe_v6) so that it uses a lazy list rather than a list. Concretely, the modified definition should use makefringe_v2 instead of makefringe_v1.
The samefringe problem, Take 4: accumulating right subtrees¶
Alternatively, we could incrementally flatten a given tree and return the leftmost payload and the list of the previous right subtrees:
let test_flatten_and_accumulate_int candidate =
let b0 = (candidate []
= None)
and b1 = (candidate [Leaf 1]
= Some (1, []))
and b2 = (candidate [Leaf 1; Leaf 2]
= Some (1, [Leaf 2]))
and b3 = (candidate [Node (Leaf 2, Leaf 3); Node (Leaf 4, Leaf 5)]
= Some (2, [Leaf 3; Node (Leaf 4, Leaf 5)]))
and b4 = (candidate [Node (Node (Node (Leaf 1, Leaf 2), Leaf 3), Leaf 4); Leaf 5]
= Some (1, [Leaf 2; Leaf 3; Leaf 4; Leaf 5]))
in b0 && b1 && b2 && b3 && b4;;
Namely:
let flatten_and_accumulate ts =
(* flatten_and_accumulate : 'a binary_tree -> ('a * 'a binary_tree list) option *)
let rec loop t ts =
match t with
| Leaf v ->
Some (v, ts)
| Node (t1, t2) ->
loop t1 (t2 :: ts)
in match ts with
| [] ->
None
| t :: ts' ->
loop t ts';;
This implementation passes the unit test:
# test_flatten_and_accumulate_int flatten_and_accumulate;;
- : bool = true
#
The corresponding samefringe function incrementally flattens the given trees and accumulates their right subtrees:
let samefringe_v7 t1 t2 =
let rec loop o1 o2 =
match o1 with
| None ->
(match o2 with
| None ->
true
| Some _ ->
false)
| Some (v1, t1s) ->
(match o2 with
| None ->
false
| Some (v2, t2s) ->
if v1 = v2
then loop (flatten_and_accumulate t1s) (flatten_and_accumulate t2s)
else false)
in loop (flatten_and_accumulate [t1]) (flatten_and_accumulate [t2]);;
And it passes the unit test too:
# test_samefringe_int rotate_binary_tree_randomly_v1 samefringe_v7;;
- : bool = true
#
The samefringe problem, Take 5: incrementally rotating the given trees to the right¶
Finally, we could trample on structural recursion and incrementally rotate the given trees to the right until the subtree on the left is a leaf:
let flatten_incrementally t =
(* flatten_incrementally : 'a binary_tree -> 'a * 'a binary_tree option *)
let rec loop t =
match t with
| Leaf v ->
(v, None)
| Node (t1, t2) ->
(match t1 with
| Leaf v1 ->
(v1, Some t2)
| Node (t11, t12) ->
loop (Node (t11, Node (t12, t2))))
in loop t;;
let samefringe_v8 t1 t2 =
let rec loop (v1, ot1) (v2, ot2) =
if v1 = v2
then match ot1 with
| None ->
(match ot2 with
| None ->
true
| Some _ ->
false)
| Some t1 ->
(match ot2 with
| None ->
false
| Some t2 ->
loop (flatten_incrementally t1) (flatten_incrementally t2))
else false
in loop (flatten_incrementally t1) (flatten_incrementally t2);;
This implementation passes the unit test too:
# test_samefringe_int rotate_binary_tree_randomly_v1 samefringe_v8;;
- : bool = true
#
Alfrothul: Structural recursion is trampled on?Harald: It sure is – look at the recursive call in loop.Alfrothul: Indeed loop isn’t applied to a smaller part of the input.Vigfus: So it doesn’t implement an induction hypothesis, does it?Brynja: And we need an external argument to show that loop terminates.
Resources¶
- The OCaml code for the present lecture note (latest version: 14 Apr 2019).
Version¶
Typo in the analysis of rotate_binary_tree_randomly_v1 fixed, thanks to Rayner Ng Jing Kai’s eagle eye [31 Mar 2020]
Traced version of samefringe_v4 added [14 Apr 2019]
Created [06 Apr 2019]