Queues

Queues are data structures that contains elements in a certain order. A queue can be empty (i.e., not contain any element), one can test whether a queue is empty or not, an element can be enqueued into a queue, and an element can be dequeued from a non-empty queue. The two canonical orders are

• last in, first out (as in a stack of pancakes: the last one pushed onto the stack is the first one to be popped off); and
• first in, first out (as in a line of customers in a shop waiting for their turn: the one who arrived first is the first one to be served).

An abstract data type

Our goal is to define the polymorphic type:

type 'a queue

together with the following operators:

• empty (of type 'a queue), the empty queue;
• is_empty (of type 'a queue -> bool), to test whether a given queue is empty or not;
• enqueue (of type 'a -> 'a queue -> 'a queue) to enqueue a given element into a given queue and return the resulting queue; and
• dequeue (of type 'a queue -> ('a * 'a queue) option) to dequeue an element from a given queue and return the resulting element and the resulting queue.

Food for thought:

• The type of enqueue is in curried form. In uncurried form, this type would read ('a * 'a queue) -> 'a queue.

• For symmetry with dequeue, one could be tempted to uncurry enqueue:

  enqueue : ('a * 'a queue) -> 'a queue
  dequeue : 'a queue -> ('a * 'a queue) option
  

  In practice, though, both forms are equivalent and OCaml encourages a curried style.

Last in, first out (LIFO)

The last element that was enqueued is the first to be dequeued. (A lifo queue is also known as a stack.)

The following unit-test function captures what it means for a queue to be last in, first out:

let test_lifo_queue_int empty is_empty enqueue dequeue =
  let b0 = (is_empty empty = true)
  and b1 = (is_empty (enqueue 3 empty) = false)
  and b2 = (match dequeue empty with
            | Some _ ->
               false
            | None ->
               true)
  and b3 = (match dequeue (enqueue 3 empty) with
            | Some (x, q) ->
               x = 3 && is_empty q
            | None ->
               false)
  and b4 = (match dequeue (enqueue 4 (enqueue 3 empty)) with
            | Some (x, q) ->
               x = 4 && (match dequeue q with
                         | Some (y, q') ->
                            y = 3 && is_empty q'
                         | None ->
                            false)
            | None ->
               false)
  (* etc. *)
  in b0 && b1 && b2 && b3 && b4;;

In words:

• the empty queue should be recognized as such;
• a non-empty queue should be recognized as such;
• the empty queue cannot be dequeued;
• enqueueing an element in the empty queue and dequeueing the resulting queue should give back this element and the empty queue;
• enqueueing several elements and repeatedly dequeueing the resulting queue should give back these elements last in, first out.

Exercise 2

1. Make sense of the other tests in the definition of test_lifo_queue_int in the accompanying file
2. Extend test_lifo_queue_int with one more test where 3 integers are enqueued.

First in, first out (FIFO)

The first element that was enqueued is the first to be dequeued.

The following unit-test function captures what it means for a queue to be first in, first out:

let test_fifo_queue_int empty is_empty enqueue dequeue =
  let b0 = (is_empty empty = true)
  and b1 = (is_empty (enqueue 3 empty) = false)
  and b2 = (match dequeue empty with
            | Some _ ->
               false
            | None ->
               true)
  and b3 = (match dequeue (enqueue 3 empty) with
            | Some (x, q) ->
               x = 3 && is_empty q
            | None ->
               false)
  and b4 = (match dequeue (enqueue 4 (enqueue 3 empty)) with
            | Some (x, q) ->
               x = 3 && (match dequeue q with
                         | Some (y, q') ->
                            y = 4 && is_empty q'
                         | None ->
                            false)
            | None ->
               false)
  (* etc. *)
  in b0 && b1 && b2 && b3 && b4;;

In words:

• the empty queue should be recognized as such;
• a non-empty queue should be recognized as such;
• the empty queue cannot be dequeued;
• enqueueing an element in the empty queue and dequeueing the resulting queue should give back this element and the empty queue;
• enqueueing several elements and repeatedly dequeueing the resulting queue should give back these elements first in, first out.

Exercise 3

1. Make sense of the other tests in the definition of test_fifo_queue_int in the accompanying file
2. Extend test_fifo_queue_int with one more test where 3 integers are enqueued.

Exercise 4

1. Implement a unit-test function for a “last in, last out” queue, and characterize this style of queues.
2. Implement a unit-test function for a “first in, last out” queue, and characterize this style of queues.

Representing a LIFO queue with a list

It is straightforward to represent a last-in, first-out queue with a list because the enqueueing and dequeueing activities happen at the same end of this list. So the empty queue can be represented with the empty list, enqueueing can be implemented with List.cons, and dequeueing non-empty queues can be implemented with List.hd and List.tl, which operate in constant time:

type 'a lifo_queue_v1 = 'a list;;

let lifo_empty_v1 =
  [];;

let lifo_is_empty_v1 q =
  match q with
  | [] ->
     true
  | _ :: _ ->
     false;;

let lifo_enqueue_v1 x q =
  x :: q;;

let lifo_dequeue_v1 q =
  match q with
  | [] ->
     None
  | x :: q' ->
     Some (x, q');;

These OCaml functions pass the unit test:

# test_lifo_queue_int lifo_empty_v1 lifo_is_empty_v1 lifo_enqueue_v1 lifo_dequeue_v1;;
- : bool = true
#

Food for thought:

• each of lifo_empty_v1, lifo_is_empty_v1, lifo_enqueue_v1, and lifo_dequeue_v1 operates in constant time.

So for example, starting with the empty queue [],

1. enqueueing 1 in this queue yields [1] in constant time;
2. enqueueing 2 in this queue yields [2; 1] in constant time;
3. enqueueing 3 in this queue yields [3; 2; 1] in constant time;
4. dequeueing this queue yields Some (3, [2; 1]) in constant time;
5. dequeueing the resulting queue yields Some (2, [1]) in constant time;
6. enqueueing 4 in the resulting queue yields [4; 1] in constant time;
7. enqueueing 5 in this queue yields [5; 4; 1] in constant time;
8. dequeueing this queue yields Some (5, [4; 1]) in constant time;
9. dequeueing the resulting queue yields Some (4, [1]) in constant time;
10. dequeueing the resulting queue yields Some (1, []) in constant time.

Representing a FIFO queue with a list

It is far less straightforward to represent a first-in, first-out queue with a list because the enqueueing and dequeueing activities happen at both ends of this list. Let us study the two obvious implementations: enqueueing by copying the current list (Version 1), and dequeueing by copying the current list (Version 2).

Representing a FIFO queue with a list, Version 1: the first (to be dequeued) shall be the first (in the list)

In this representation, the queue is a list of elements where the last element in this list shall be the last to be dequeued:

type 'a fifo_queue_v1 = 'a list;;

let fifo_empty_v1 =
  [];;

let fifo_is_empty_v1 q =
  q = [];;

let fifo_enqueue_v1 x q =
  let rec prepend q =
    match q with
    | [] ->
       [x]
    | x' :: q' ->
       x' :: prepend q'
  in prepend q;;

let fifo_dequeue_v1 q =
  match q with
  | [] ->
     None
  | x :: q' ->
     Some (x, q');;

These OCaml functions pass the unit test:

# test_fifo_queue_int fifo_empty_v1 fifo_is_empty_v1 fifo_enqueue_v1 fifo_dequeue_v1
- : bool = true
#

Food for thought:

• each of fifo_empty_v1, fifo_is_empty_v1, and fifo_dequeue_v1 operates in constant time;

• fifo_enqueue_v1 operates in time and space proportional to the given queue, i.e., in linear time;

• fifo_enqueue_v1 could be defined more concisely as follows:

  let fifo_enqueue_v1 x q =
    List.append q [x];;
  

• using the infix operator @ that stands for list concatenation, fifo_enqueue_v1 could be defined even more briefly as follows:

  let fifo_enqueue_v1 x q =
    q @ [x];;
  

So for example, starting with the empty queue [],

1. enqueueing 1 in this queue yields [1] in linear time ([] is prepended to [1]);
2. enqueueing 2 in this queue yields [1; 2] in linear time ([1] is prepended to [2]);
3. enqueueing 3 in this queue yields [1; 2; 3] in linear time ([1; 2] is prepended to [3]);
4. dequeueing this queue yields Some (1, [2; 3]) in constant time;
5. dequeueing the resulting queue yields Some (2, [3]) in constant time;
6. enqueueing 4 in the resulting queue yields [3; 4] in linear time ([3] is prepended to [4]);
7. enqueueing 5 in this queue yields [3; 4; 5] in linear time ([3; 4] is prepended to [5]);
8. dequeueing this queue yields Some (3, [4; 5]) in constant time;
9. dequeueing the resulting queue yields Some (4, [5]) in constant time;
10. dequeueing the resulting queue yields Some (5, []) in constant time.

Representing a FIFO queue with a list, Version 2: the first (to be dequeued) shall be the last (in the list)

In this representation, the queue is a list of elements where the first element in this list shall be the last to be dequeued:

type 'a fifo_queue_v2 = 'a list;;

let fifo_empty_v2 =
  [];;

let fifo_is_empty_v2 q =
  q = [];;

let fifo_enqueue_v2 x q =
  x :: q;;

let fifo_dequeue_v2 q =
  match q with
  | [] ->
     None
  | x :: q' ->
     let rec traverse x q =
       match q with
       | [] ->
          (x, [])
       | x' :: q' ->
          let (last_element, prefix) = traverse x' q'
          in (last_element, x :: prefix)
     in Some (traverse x q');;

These OCaml functions pass the unit test:

# test_fifo_queue_int fifo_empty_v2 fifo_is_empty_v2 fifo_enqueue_v2 fifo_dequeue_v2;;
- : bool = true
#

Food for thought:

• each of fifo_empty_v2, fifo_is_empty_v2, and fifo_enqueue_v2 operates in constant time;
• fifo_dequeue_v2 operates in time and space proportional to the given queue, i.e., in linear time;

So for example, starting with the empty queue [],

1. enqueueing 1 in this queue yields [1] in constant time;
2. enqueueing 2 in this queue yields [2; 1] in constant time;
3. enqueueing 3 in this queue yields [3; 2; 1] in constant time;
4. dequeueing this queue yields Some (1, [3; 2]) in linear time;
5. dequeueing the resulting queue yields Some (2, [3]) in linear time;
6. enqueueing 4 in the resulting queue yields [4; 3] in constant time;
7. enqueueing 5 in this queue yields [5; 4; 3] in constant time;
8. dequeueing this queue yields Some (3, [5; 4]) in linear time;
9. dequeueing the resulting queue yields Some (4, [5]) in linear time;
10. dequeueing the resulting queue yields Some (5, []) in linear time.

Representing a FIFO queue with a list, Version 3: amortizing space and time opportunistically

The lists representing the queues are reverse of each other in Versions 1 and 2, and this representation incurs a linear cost, either to enqueue (in Version 1), or to dequeue (in Version 2).

Positing that the common case is that consecutive queue operations are the same, i.e., several enqueueing operations in a row, followed by several dequeueing operations in a row, let us adopt a flipped representation of the queue as a list indexed by a Boolean:

type 'a fifo_queue_v3 = bool * 'a list;;

The key idea is threefold:

1. if the Boolean is true, the list is in one order and enqueueing is cheap, and if the Boolean is false, the list is in the reverse order and dequeueing is cheap;
2. the Boolean reflects the last operation on the queue: true if an element was enqueued, and false if an element was dequeued;
3. if the new operation on the queue is the same as the last one, then it is carried out in constant time; and if the new operation on the queue is not the same as the last one (i.e., enqueue instead of dequeue, or dequeue instead of enqueue), the list is reversed so that the operation can be carried out in constant time, and the Boolean is flipped.

This way, the linear cost only occurs when the queue shifts from being enqueued to being dequeued, and from being dequeued to being enqueued, instead of each time the queue is enqueued (in Version 1) or each time the queue is dequeued (in Version 2):

type 'a fifo_queue_v3 = bool * 'a list;;

let fifo_empty_v3 =
  (true, []);;

let fifo_is_empty_v3 q =
  match q with
  | (_, []) ->
     true
  | (_, _ :: _) ->
     false;;

let fifo_enqueue_v3 x (flag, xs) =
  let xs = if flag
           then xs
           else List.rev xs
  in (true, x :: xs);;

let fifo_dequeue_v3 (flag, xs) =
  let xs = if flag
           then List.rev xs
           else xs
  in match xs with
       | [] ->
          None
       | x :: xs' ->
          Some (x, (false, xs'));;

These OCaml functions pass the unit test:

# test_fifo_queue_int fifo_empty_v3 fifo_is_empty_v3 fifo_enqueue_v3 fifo_dequeue_v3;;
- : bool = true
#

Food for thought:

• each of fifo_empty_v3 and fifo_is_empty_v3 operates in constant time;
• if the Boolean is true, fifo_enqueue_v3 operates in constant time and fifo_dequeue_v3 operates in linear time; and
• if the Boolean is false, fifo_dequeue_v3 operates in constant time and fifo_enqueue_v3 operates in linear time.

So for example, starting with the empty queue (true, []),

1. enqueueing 1 in this queue yields (true, [1]) in constant time;
2. enqueueing 2 in this queue yields (true, [2; 1]) in constant time;
3. enqueueing 3 in this queue yields (true, [3; 2; 1]) in constant time;
4. dequeueing this queue yields Some (1, (false, [2; 3])) in linear time;
5. dequeueing the resulting queue yields Some (2, (false, [3])) in constant time;
6. enqueueing 4 in the resulting queue yields (true, [4; 3]) in linear time;
7. enqueueing 5 in this queue yields (true, [5; 4; 3]) in constant time;
8. dequeueing this queue yields Some (3, (false, [4; 5]) in linear time;
9. dequeueing the resulting queue yields Some (4, (false, [5])) in constant time;
10. dequeueing the resulting queue yields Some (5, (false, [])) in constant time.

Each time the Boolean changes, there is a linear cost.

Representing a FIFO queue with a list, Version 4: amortizing space and time structurally

During his PhD studies, Chris Okasaki proposed an even more radical idea: to represent the queue as a pair of lists:

• the first list to dequeue from in constant time, and
• the second list to enqueue to in constant time.

The key point was to reverse the second list and make it the first when the first list runs out of elements to dequeue:

type 'a fifo_queue_v4 = 'a list * 'a list;;

let fifo_empty_v4 =
  ([], []);;

let fifo_is_empty_v4 q =
  q = ([], []);;

let fifo_enqueue_v4 x (pool, reversed_prefix) =
  (pool, x :: reversed_prefix);;

let fifo_dequeue_v4 (pool, reversed_prefix) =
  match pool with
  | [] ->
     (match List.rev reversed_prefix with
      | [] ->
         None
      | x :: new_pool ->
         Some (x, (new_pool, [])))
  | x :: pool' ->
     Some (x, (pool', reversed_prefix));;

These OCaml functions pass the unit test:

# test_fifo_queue_int fifo_empty_v4 fifo_is_empty_v4 fifo_enqueue_v4 fifo_dequeue_v4;;
- : bool = true
#

Food for thought:

• each of fifo_empty_v4 and fifo_is_empty_v4 operates in constant time;
• fifo_enqueue_v4 operates in constant time; and
• if the first list is empty, fifo_dequeue_v4 operates in linear time over the second list.
• if the first list is non-empty, fifo_dequeue_v4 operates in constant time.

So for example, starting with the empty queue ([], []),

1. enqueueing 1 in this queue yields ([], [1]) in constant time;
2. enqueueing 2 in this queue yields ([], [2; 1]) in constant time;
3. enqueueing 3 in this queue yields ([], [3; 2; 1]) in constant time;
4. dequeueing this queue yields Some (1, ([2; 3], [])) in linear time;
5. dequeueing the resulting queue yields Some (2, ([3], [])) in constant time;
6. enqueueing 4 in the resulting queue yields ([3], [4]) in constant time;
7. enqueueing 5 in this queue yields ([3], [5; 4]) in constant time;
8. dequeueing this queue yields Some (3, ([], [5; 4])) in constant time;
9. dequeueing the resulting queue yields Some (4, ([5], [])) in linear time;
10. dequeueing the resulting queue yields Some (5, ([], [])) in constant time.

Representing a FIFO queue with a list, Version 5: a functional representation

Version 5 is a mild variation of Version 4 where the second list is represented as a function:

type 'a fifo_queue_v5 = 'a list * ('a list -> 'a list);;

let cons x xs =
  x :: xs;;

let compose f g x =
  f (g x);;

let fifo_empty_v5 =
  ([], fun es -> es);;

let fifo_is_empty_v5 (es, h) =
  es = [] && h [] = [];;

let fifo_enqueue_v5 x (pool, h) =
  (pool, compose h (cons x));;

let fifo_dequeue_v5 (pool, h) =
  match pool with
  | [] ->
     (match h [] with
      | [] ->
         None
      | x :: new_pool ->
         Some (x, (new_pool, fun es -> es)))
  | x :: pool' ->
     Some (x, (pool', h));;

These OCaml functions pass the unit test:

# test_fifo_queue_int fifo_empty_v5 fifo_is_empty_v5 fifo_enqueue_v5 fifo_dequeue_v5;;
- : bool = true
#

Food for thought:

• fifo_empty_v5 operates in constant time;
• fifo_is_empty_v5 operates in linear time;
• fifo_enqueue_v5 operates in constant time; and
• if the first list is empty, fifo_dequeue_v5 operates in linear time.
• if the first list is non-empty, fifo_dequeue_v5 operates in constant time.

So for example, starting with the empty queue ([], h0), where h0 denotes a function that maps [] to [],

1. enqueueing 1 in this queue yields ([], h1) in constant time, where h1 denotes a function that maps [] to [1];
2. enqueueing 2 in this queue yields ([], h2) in constant time, where h2 denotes a function that maps [] to [1; 2];
3. enqueueing 3 in this queue yields ([], h3) in constant time, where h3 denotes a function that maps [] to [1; 2; 3];
4. dequeueing this queue yields Some (1, ([2; 3], h0)) in linear time, where h0 denotes a function that maps [] to [];
5. dequeueing the resulting queue yields Some (2, ([3], h0)) in constant time;
6. enqueueing 4 in the resulting queue yields ([3], h4) in constant time, where h4 denotes a function that maps [] to [4];
7. enqueueing 5 in this queue yields ([3], h5) in constant time, where h5 denotes a function that maps [] to [4; 5];
8. dequeueing this queue yields Some (3, ([], h5)) in constant time;
9. dequeueing the resulting queue yields Some (4, ([5], h0)) in linear time;
10. dequeueing the resulting queue yields Some (5, ([], h0)) in constant time.

Exercise 5

Clone Version 5 of the code above into a Version 6 where in the definition of the enqueue operation, (cons v) is composed on the left of h instead of on the right:

let fifo_enqueue_v6 x (pool, h) =
  (pool, compose (cons x) h);;

Which kind of queue does Version 6 implement? A known one? A new one? Why?

Exercise 6

Fix Version 5 so that fifo_is_empty_v5 operates in constant time.

Exercise 7

In the resource file for the present lecture note, a type of binary tree is defined with a payload in the leaves:

type 'a binary_tree =
  | Leaf of 'a
  | Node of 'a binary_tree * 'a binary_tree;;

Four tree-traversing functions are defined that collect the payloads into a list:

• traverse_foo_lifo,
• traverse_foo_fifo,
• traverse_bar_lifo, and
• traverse_bar_fifo.

Look at the output of these tree-traversing functions, characterize the traversal that each of these functions implements, and test your characterization with 4 new telling examples.

You should return

1. a crisp, concise description of your characterization in English, and
2. your 4 telling examples, along with a brief explanation of why you find them telling.

Friendly hints:

1. draw some binary trees based on the convention that in Node (t1, t2), t1 denotes the left subtree and t2 denotes the right subtree. For example, the tree Node (Node (Leaf 3, Leaf 9), Leaf 5) is depicted as follows:

   

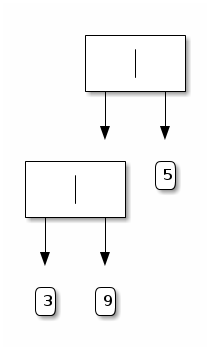
2. use the traced versions of traverse_foo_lifo, traverse_foo_fifo, traverse_bar_lifo, and traverse_bar_fifo provided in the resource file to visualize what is going on.

Subsidiary (and optional) questions:

1. Neither traverse_foo nor traverse_bar are structurally recursive (and so could not be written using fold_binary_tree). Why is that?
2. Could you write a version of traverse_foo_lifo that is structurally recursive (and so could be written using fold_binary_tree)? If so, do it. Otherwise, say why.
3. Could you write a version of traverse_foo_fifo that is structurally recursive (and so could be written using fold_binary_tree)? If so, do it. Otherwise, say why.
4. Could you write a version of traverse_bar_lifo that is structurally recursive (and so could be written using fold_binary_tree)? If so, do it. Otherwise, say why.
5. Could you write a version of traverse_bar_fifo that is structurally recursive (and so could be written using fold_binary_tree)? If so, do it. Otherwise, say why.

Resources

• The OCaml code for the present lecture note (latest version: 08 Apr 2020).

Version

Fixed a typo in the narrative, thanks to Sviatlana Yasiukova’s eagle eye [07 Apr 2019]

Polished the narrative [02 Apr 2019]

Created [31 Mar 2019]