Kleene’s S-m-n theorem

Programs hacking programs. Why?

—Thomas A. Anderson

So language processors are programs that process other programs: an interpreter runs a program, and a compiler translates a source program into a target program. Are there other such programs that process other programs?

Exercise 1

Analyze the quip “One person’s program is another program’s data.”, from its origins (“Quod ali cibus est aliis fuat acre venenum.” and “One man’s meat is another man’s poison.”) to its significance here.

Programs and the function they compute

If a program p written in L computes a function f, then p and f are related using an interpreter for L (let’s name it run):

run p = f

Neil Jones: Yes.

Mimer: Prof. Jones, thanks for stopping by!

Then we say that f is computable.

Conversely, if a function is computable, then a program exists that computes it.

For example, consider the factorial function that maps 0 to 1 and that maps a positive integer n to 1 * 2 * ... (n - 1) * n. The factorial function is computable: we can (and we will) implement it, i.e., we will write a program that computes the factorial function. Let fac denote this program. Running it on the input 5 should yield 120 since 5! = 120:

run fac 5 = 120

When a program is computable, the meaning of this program is the function computed by this program.

Not all functions, however, are computable: no programs exist that compute them. These functions are uncomputable: we cannot implement them.

For example, consider the halting predicate (i.e., a function that returns a Boolean) that, given a program and its input, returns true if running this program on this input terminates and false if it doesn’t. This function is uncomputable: we cannot implement it.

Interlude about the halting predicate

Harald: Uncomputable?

Alfrothul: That’s what was said.

Harald: How so?

Alfrothul: Good question.

Brynja: Well, the existence of a halting predicate would entail a paradox?

Alfrothul: OK, I remember Cyrano de Bergerac and Pinocchio (Exercise 17 in Week 01). Paradox in what sense?

Brynja: Well, suppose that this program exists.

Harald: A program that computes the halting predicate, yes.

Brynja: And suppose that a diverging subprogram exists: executing it does not terminate.

Harald: OK.

Brynja: Now imagine the following computation. Given a program and its input, test whether running this program on this input terminates, using the halting predicate. If it does, then execute the diverging subprogram; and otherwise, terminate.

Alfrothul: OK.

Brynja: Does this computation terminate?

Harald: Well, there are two possibilities: either running the given program on the given input terminates, or it doesn’t.

Alfrothul: First case: running the given program terminates. Then we execute the diverging subprogram. OK, in that case the computation doesn’t terminate since executing the diverging subprogram does not terminate.

Vigfus: Second case: running the given program does not terminate. Then we terminate. OK, in that case the computation terminates.

Harald: To sum up, if running the given program on the given input terminates, then the computation does not terminate, and if running the given program on the given input does not terminate, then the computation terminates. It feels like a big negation.

Brynja (steadfast): Maybe it does. Now consider the program implementing this computation.

Harald: Aha: this program is given another program and its input.

Brynja: Right. Given this other program and its input, running this other program on its input achieves the computation that you just characterized as a big negation. Now let’s say that this other program is this program, i.e., let’s apply this program to itself.

Halcyon (sententiously): A process known as diagonalization.

Vigfus (excitedly): clickety clickety click. Guys, did you see that the Wikipedia entries Diagonal argument and Diagonal argument (disambiguation) point to each other?

Brynja (undaunted): Of course they do. But the question here is whether applying the program to itself terminates.

Harald: Well, we face the same two possibilities: either running the given program—let me still call it the given program, even though it is the same program—on its input terminates or it doesn’t.

Alfrothul: First case: running the given program on the given input terminates. As we have seen above, the computation doesn’t terminate, and therefore running the given program on the given input doesn’t terminate since this program implements the computation.

Vigfus: Second case: running the given program on the given input does not terminate. As we have seen above, the computation terminates, and therefore running the given program on the given input terminates since this program implements the computation.

Alfrothul: OK, a paradox, since the given program is the program. If running it terminates, then running it doesn’t terminate, and if running it doesn’t terminate, then running it terminates.

Brynja: Right.

Pinocchio: AT-CHOO!

Brynja (undeterred): So the halting predicate is uncomputable.

Mimer: Put otherwise, the halting problem is undecidable: given an arbitrary program and its input, we cannot determine whether executing this program on this input terminates.

Cyrano: Thank you.

Aftermath

Harald: I guess this answers the question.

Alfrothul: Sorry. What answers which question?

Harald: The question as to whether there are programs that process other programs and that are not interpreters or compilers.

Alfrothul: Oh, you mean the program that implements the halting predicate?

Harald: Yes: this halting program is given another program, to test whether this other program terminates.

Alfrothul: But the halting program doesn’t exist, we just showed that.

Harald: Harrumph.

Kleene’s S-m-n function

Consider a program p that takes m + n inputs and returns a result:

run p (x1, x2, ..., xm, y1, y2, ..., yn) = result

Kleene‘s S-m-n function (written S-m-n), given p and the m first inputs, produces program q that, given the remaining n inputs, returns the same result as the original program over the whole input:

S-m-n (p, (x1, x2, ..., xm)) = q
    run q (y1, y2, ..., yn)  = result

A few remarks:

• p is often said to be the source program, and q the residual program.

• q is a version of p that is specialized with respect to the m first inputs; as such the S-m-n function specializes p with respect to the m first inputs.

• If m is 0, then q is p:

             S-0-n (p, ()) = q
  run q (y1, y2, ..., yn)  = result
  

• If n is 0, then q is the constant program that always returns result:

  S-m-0 (p, (x1, x2, ..., xm)) = q
                     run q ()  = result
  

The S-m-n function is appealing because a residual program may not only be a specialized version of a source program, it may be a simplified version of it. For example, suppose that m >= 2 and p contains a + b, where a and b are p‘s first and second parameters. As such, given x1 and x2, we know that a denotes x1 and b denotes x2: so in the residual program, a + b can be replaced by the result of adding x1 and x2. In the extreme case where n = 0, all the computations of p can be simplified into result. The residual program is then a lot more efficient than the source program since it performs no computations at all: it just returns the result.

Concretely, say that p is a program with 3 inputs, x1, x2, and x3, that computes 0 + (1 + x1) + (x2 + 1000) + x3. Executing this program on 3 arguments, 10, 100 and 10000, induces the computation of 0 + (1 + 10) + (100 + 1000) + 10000 and yields 11111:

run p (10, 100, 10000) = 11111

• Say that we specialize p with respect to 0 inputs:

  S-0-3 (p, ()) = q
  

  The residual program, q, is a program with 3 inputs, x1, x2, and x3, that computes (1 + x1) + (x2 + 1000) + x3, assuming that the addition with 0 has been simplified away. Executing this program on 3 arguments, 10, 100 and 10000, induces the computation of (1 + 10) + (100 + 1000) + 10000 and yields 11111:

  run q (10, 100, 10000) = 11111
  

• Say that we specialize p with respect to 1 input, 10:

  S-1-2 (p, (10)) = q
  

  The residual program, q, is a program with 2 inputs, x2 and x3, that computes 11 + (x2 + 1000) + x3, assuming that 0 + (1 + 10) has been simplified to 11. Executing this program on 2 arguments, 100 and 10000, induces the computation of 11 + (100 + 1000) + 10000 and yields 11111:

  run q (100, 10000) = 11111
  

• Say that we specialize p with respect to 2 inputs, 1 and 10:

  S-2-1 (p, (1, 10)) = q
  

  The residual program, q, is a program with 1 inputs, x3, that computes 1111 + x3, assuming that 0 + (1 + 10) + (100 + 1000) has been simplified to 1111. Executing this program on 1 argument, 10000, induces the computation of 1111 + 10000 and yields 11111:

  run q (10000) = 11111
  

• Say that we specialize p with respect to 3 inputs, 1, 10 and 10000:

  S-3-0 (p, (1, 10, 10000)) = q
  

  The residual program, q, is a program with 0 inputs that computes 11111, assuming that 0 + (1 + 10) + (100 + 1000) + 10000 has been simplified to 11111. Executing this program on 0 arguments induces the computation of 11111 and yields 11111:

  run q () = 11111
  

In general, though, m and n are not 0, but the idea still applies. In the rest of this lecture note, and without loss of generality, we let m and n be 1, for simplicity. In other words, from here on, we use the S-1-1 function.

The characteristic equations then read:

run p (x, y) = result
S-1-1 (p, x) = p_x
   run p_x y = result

where we wrote p_x instead of q to convey that the residual program (i.e., the result of S-1-1) is a version of p that is specialized with respect to x.

Say we need to carry out the following runs:

run p (x, a)
run p (x, b)
run p (x, c)

where a, b, and c are 3 distinct inputs. During these runs, all of the computations of p are carried out, both those that depend on x and those that depend on the second input. Alternatively, let us first specialize p with respect to x:

S-1-1 (p, x) = p_x

The following runs then proceed as follows:

run p_x a
run p_x b
run p_x c

Assume that S-1-1 has carried out all the computations of p that depend on x. These computations are carried out once, and in the subsequent runs, only the remaining computations of p (those that depend on the second input) are carried out: p_x is therefore more efficient than p since to obtain the same result, it carries out fewer computations:

run p_x a = run p (x, a)
run p_x b = run p (x, b)
run p_x c = run p (x, c)

Here are some concrete examples:

• A cookbook

  A cookbook contains many recipes. The recipe for omelets, for example, says that the cook needs 2 eggs per person.

  An ordinary editor would publish this book, e.g., with the title “Good recipes for the whole family”.

  In addition, an enterprising editor would:

  • specialize the recipes from being for an arbitrary number of people to being just for two persons; the specialized recipe for omelets, for example, would say that the cook needs 4 eggs; and
  • collect these specialized recipes in a book and publish it with the title “Happy recipes for you and me”.

  This enterprising editor could also:

  • specialize the recipes from being for an arbitrary number of people to being just for one person; the specialized recipe for omelets, for example, would say that the cook needs 2 eggs; and
  • collect these specialized recipes in a book and publish it with the title “Lonely but healthy recipes”.

  This enterprising editor could equally well:

  • specialize selected recipes to using a reduced number of dishes; and
  • collect these specialized recipes in a book and publish it with the title “Healthy recipes for students”, on the ground that students typically live in small places. (The title says “Healthy” so that the parents of the said students buy this book as a parting gift for their progeny as it leaves home for college.)

  But why stop there? Why not select recipes that don’t involve any cooking and publish several books (one for the family, one for you and me, one for single people, one for students) with the titles “The book of healthy salads”, “Healthy salads for the whole family”, “Healthy salads for you and me”, “Lonely but healthy salads”, and “Healthy salads for healthy students”, for example. Also, why not dividing the recipes with seasonal ingredients and publish 4 books, nay, a multiple of 4 books: “Healthy salads in the spring”, “Summer dreams of cooking for you and me”, “Autumn leaves, let’s eat well”, “Winter recipes for the healthy student”, etc.

  Truly, the S-m-n function offers a wealth of opportunities. And if the enterprising editor knows how to use Aristotle’s 4 causes in the titles, well, the sky is the limit.

Halcyon: A lot?

Vigfus: A lot.

Halcyon: OK.

• Matrix multiplication

  A matrix aggregates a lot of numbers, and multiplying two matrices involves multiplying these numbers, like, a lot.

  Say that matrix_multiply is a program that multiplies two matrices and yields a resulting matrix:

  run matrix_multiply (M1, M2) = M3
  

  A hollow matrix is a matrix containing many 0’s. Since 0 is absorbing for multiplication (i.e., since for any n, 0 * n = 0 and n * 0 = 0), multiplying a hollow matrix and another matrix results in a hollow matrix. Specializing a matrix-multiplication program with respect to a hollow matrix is likely to yield a specialized program that only performs the computations that do not involve 0 over the other matrix, i.e., a more efficient program.

  So let us instantiate the characteristic equations:

  run p (x, y) = result
  S-1-1 (p, x) = p_x
     run p_x y = result
  

  with

  • matrix_multiply for p,
  • M1 for x,
  • M2 for y, and
  • M3 for result.

  The result reads:

  run matrix_multiply (M1, M2) = M3
   S-1-1 (matrix_multiply, M1) = matrix_multiply_M1
    run matrix_multiply_M1 M2  = M3
  

  The specialized program matrix_multiply_M1 is a matrix multiplier dedicated to M1.

• Parsing

  Given a grammar g and a text t, a general parser GP decides whether the text is grammatically correct:

  run GP (g, t) = result
  

  Typically, we have many texts to parse given the same grammar, and presumably a lot of computations in GP depend on g. Specializing a general parser with respect to a grammar is likely to give a specialized program that only performs the computations that involve the text to parse.

  So let us instantiate the characteristic equations:

  run p (x, y) = result
  S-1-1 (p, x) = p_x
     run p_x y = result
  

  with

  • GP for p,
  • g for x,
  • t for y, and
  • result for result.

  The result reads:

  run GP (g, t) = result
  S-1-1 (GP, g) = GP_g
    run GP_g t  = result
  

  The specialized program GP_g is a parser dedicated to g.

• Unparsing

  Given a composite value v and a directive d to map this value to a textual representation, we implement an unparser:

  run unparse (d, v) = text
  

  (In a programming language such as C, this unparser is named sprintf.)

  Typically, we have many values to unparse given the same directive, and presumably a lot of computations in unparse depend on d. Specializing an unparser with respect to a directive is likely to give a specialized program that only performs the computations that involve the value to unparse.

  So let us instantiate the characteristic equations:

  run p (x, y) = result
  S-1-1 (p, x) = p_x
     run p_x y = result
  

  with

  • unparse for p,
  • d for x,
  • v for y, and
  • test for result.

  The result reads:

  run unparse (d, v) = text
  S-1-1 (unparse, d) = unparse_d
     run unparse_d v = text
  

  The specialized program is an unparser dedicated to d.

In programming,

everything we do is a special case of something more general,

– and often we know it too quickly.

—Alan Perlis‘s programming epigram #30

Interlude

Harald (wondering): Wouldn’t it be nice if the S-m-n function were computable?

I-diagrams, revisited

So an interpreter is a program for running another program. For example, let’s say we are given:

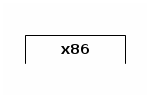
1. an x86 microprocessor, denoted run^x86 and depicted as follows:

   

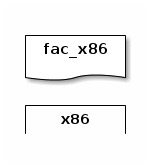
2. a program that computes the factorial function and that is written in x86, denoted by fac_x86 and depicted as follows:

   

We depict the execution of fac_x86 by putting the two pictures on top of each other:

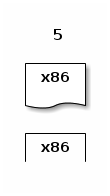
And we depict the running of fac_x86 on 5:

run^x86 fac_x86 5

by superimposing 5 on fac_x86:

This superimposition is consistent with interpreters executing other interpreters. For example, say we are given two more artifacts:

• an interpreter for OCaml written in x86, denoted run^OCaml_x86:

  

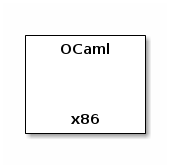
• a program that computes the factorial function and that is written in OCaml, denoted by fac_OCaml:

  

We depict the running of fac_OCaml on 5 by superimposing 5 on fac_OCaml, which is itself superimposed on run_x86^OCaml, which is itself superimposed on run^x86:

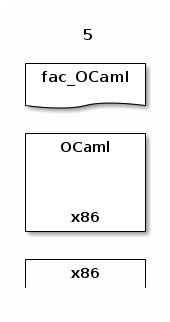
Algebraically:

run^x86 run_x86^OCaml fac_OCaml 5

As such, the following OCaml processor:

can be defined algebraically as:

run^OCaml = run^x86 run_x86^OCaml

Program equivalence

Two programs are equivalent when they have the same meaning. In the example just above, fac_OCaml and fac_x86 are equivalent because they both compute the factorial function. In other words, running fac_OCaml and fac_x86 on the same non-negative integer n yields the same result:

run^OCaml fac_OCaml n = run^x86 fac_x86 n

And a compiler is meaning preserving in that it translates a source program into an equivalent target program:

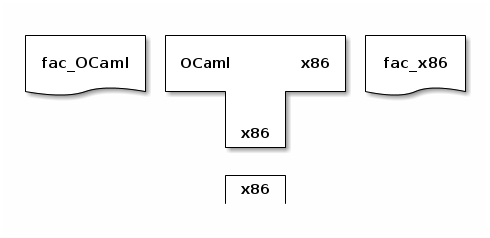
In this light, let us revisit the characteristic equations of the S-1-1 function:

run p (x, y) = result
S-1-1 (p, x) = p_x
   run p_x y = result

The first and the third equations say that given p, x, and y, we can equivalently run p on x and y or run p_x on y to obtain result.

Exercise 2

Given a source program source_program and its input input, an interpreter interpreter executes source_program on input:

run interpreter (source_program, input) = output

Typically, we run source_program on several inputs, not just one. So it is a good idea to specialize interpreter with respect to a given source_program.

To be concrete, say that interpreter is an interpreter for Python written in OCaml, and that the S-m-n function specializes a program written in OCaml into another program written in OCaml.

Questions:

1. In which language is source_program written?
2. Apply the S-1-1 function appropriately to specialize interpreter with respect to source_program, and characterize its result.

Hint towards solving Exercise 2

2. You need to instantiate the characteristic equations:

   run p (x, y) = result
   S-1-1 (p, x) = p_x
      run p_x y = result
   

   with:

   • interpreter for p
   • source_program for x
   • input for y
   • output for result

And then the questions are:

• in which language is interpreter_source_program written?
• what is interpreter_source_program, i.e., what does it do when it is executed?
• what is the relation between source_program and interpreter_source_program?

Kleene’s S-m-n theorem

Harald: Ha!

Kleene’s S-m-n theorem states that the S-m-n function is computable. Therefore a program exists that computes it. This program is traditionally referred to as a “program specializer” (for what it does) and as a “partial evaluator” (for how it does it, since it evaluates part of the source program to specialize it with respect to the given part of the input). Because of the latter point, its traditional name is PE:

run PE = S-m-n

So given a program p that takes m + n inputs and returns a result:

run p (x1, x2, ..., xm, y1, y2, ..., yn) = result

a partial evaluator, given p and the m first inputs, produces program q that, given the remaining n inputs, returns the same result as the original program over the whole input:

run PE (p, (x1, x2, ..., xm)) = q
     run q (y1, y2, ..., yn)  = result

Harald: So it looks like one program’s variable...

Alfrothul: ...is another program’s constant.

Alan Perlis: Sounds about right. Do you guys need a chairperson?

Mimer: Prof. Perlis, thanks for stopping by! And thanks for your epigrams too!

Exercise 3

Write down the four causes of a partial evaluator.

Exercise 4

Partial evaluation is what a partial evaluator does.

Write down as many as you like of the four causes of partial evaluation, in the order of your choosing:

• material cause
• efficient cause
• formal cause
• final cause

How does your solution compare with the four causes of a partial evaluator, in Exercise 3?

Exercise 5

Revisit the four examples above (matrix multiplication, parsing, unparsing, and the interpreter exercise) using PE instead of S-1-1:

run PE = S-1-1

Partial solution for Exercise 5

The first step is to state the characteristic equations using PE instead of S-1-1:

 run p (x, y) = result
run PE (p, x) = p_x
    run p_x y = result

Food for thought

In the vein of I- and T-diagrams, and assuming that PE computes S-1-1, can you think of a diagram that would usefully depict PE?

Specializing the partial evaluator with respect to the program to specialize

Again for simplicity, in this section, PE computes the S-1-1 function.

Suppose that we are in a situation where we need to specialize the same program with respect to a variety of partial inputs:

run PE (p, x) = p_x

Then de facto we are going to run PE many times over p, an opportunity for the S-1-1 function. So let us instantiate the characteristic equations:

run p (x, y) = result
S-1-1 (p, x) = p_x
   run p_x y = result

with

• PE for p,
• p for x,
• x for y, and
• p_x for result.

The result reads:

run PE (p, x) = p_x
S-1-1 (PE, p) = PE_p
   run PE_p x = p_x

The specialized program PE_p is a program specializer that is dedicated to specializing p. And indeed running p_x on y gives the same result as running p on both x and y:

run p_x y  = run p (x, y)

Using PE instead of S-1-1:

 run PE (p, x) = p_x
run PE (PE, p) = PE_p
    run PE_p x = p_x

Halcyon: Diagonalization, here we come again.

Vigfus: True that—the partial evaluator is operating on itself.

Alfrothul (picky): On a copy of itself.

Here are some concrete examples:

• Matrix multiplication

  To specialize the program specializer with respect to a matrix-multiplication program, let us instantiate the characteristic equations:

   run PE (p, x) = p_x
  run PE (PE, p) = PE_p
      run PE_p x = p_x
  

  with

  • matrix_multiply for p and
  • M1 for x.

  The result reads:

  run PE (matrix_multiply, M1) = matrix_multiply_M1
  run PE (PE, matrix_multiply) = PE_matrix_multiply
     run PE_matrix_multiply M1 = matrix_multiply_M1
  

  This result could also be obtained as an instance of the characteristic equations:

   run p (x, y) = result
  run PE (p, x) = p_x
      run p_x y = result
  

  with

  • PE for p,
  • matrix_multiply for x,
  • M1 for y, and
  • matrix_multiply_M1 for result.

  The specialized program PE_matrix_multiply is a program specializer that is dedicated to specializing matrix_multiply. And indeed running matrix_multiply_M1 on M2 gives the same result as running matrix_multiply on both M1 and M2:

  run matrix_multiply_M1 M2 = run matrix_multiply (M1, M2)
  

• Parsing

  To specialize the program specializer with respect to a general parser, let us instantiate the characteristic equations:

   run PE (p, x) = p_x
  run PE (PE, p) = PE_p
      run PE_p x = p_x
  

  with

  • GP for p and
  • g for x.

  The result reads:

   run PE (GP, g) = GP_g
  run PE (PE, GP) = PE_GP
      run PE_GP g = GP_g
  

  This result could also be obtained as an instance of the characteristic equations:

   run p (x, y) = result
  run PE (p, x) = p_x
      run p_x y = result
  

  with

  • PE for p,
  • GP for x,
  • g for y, and
  • GP_g for result.

  The specialized program PE_GP is a program specializer that is dedicated to specializing GP. And indeed running GP_g on t gives the same result as running GP on both g and t:

  run GP_g t = run GP (g, t)
  

• Unparsing

  Let us specialize the program specializer with respect to an unparser, let us instantiate the characteristic equations:

   run PE (p, x) = p_x
  run PE (PE, p) = PE_p
      run PE_p x = p_x
  

  with

  • unparse for p and
  • d for x.

  The result reads:

   run PE (unparse, d) = unparse_d
  run PE (PE, unparse) = PE_unparse
      run PE_unparse d = unparse_d
  

  This result could also be obtained as an instance of the characteristic equations:

   run p (x, y) = result
  run PE (p, x) = p_x
      run p_x y = result
  

  with

  • PE for p,
  • unparse for x,
  • d for y, and
  • unparse_d for result.

  The specialized program PE_unparse is a program specializer that is dedicated to specializing unparse. And indeed running unparse_d on v gives the same result as running unparse on both d and v:

  run unparse_d v = run unparse (d, v)
  

Exercise 6

As a continuation of Exercise 2, specialize the program specializer with respect to interpreter, and characterize the resulting specialized program specializer: what does it do?

(To be concrete, say that PE is a program written in OCaml.)

Exercise 7

The goal of this exercise is to revisit the equation:

run PE (PE, p) = PE_p

in the particular case where p is PE itself, and to characterize the resulting program, PE_PE.

1. What is the result of applying PE_PE to matrix-multiply?
2. What is the result of applying PE_PE to GP?
3. What is the result of applying PE_PE to unparse?
4. What is the result of applying PE_PE to interpreter, as a continuation of Exercise 2 and Exercise 6?
5. What is the result of applying PE_PE to PE?

Partial solution for Exercise 7

If p is PE itself, the equation reads:

run PE (PE, PE) = PE_PE

1. This case reads:

   run PE_PE matrix_multiply = result
   

   which is an instance of the third characteristic equation:

    run p (x, y) = result
   run PE (p, x) = p_x
       run p_x y = result
   

   with

   • PE for p,
   • PE for x, and
   • matrix_multiply for y

   and where we are asked to describe what result denotes.

   Quoting the above:

   The specialized program PE_p is a program specializer that is dedicated to specializing p. And indeed running p_x on y gives the same result as running p on both x and y:

   run p_x y  = run p (x, y)
   

   Let us instantiate this quote with PE instead of p, PE instead of x, and matrix_multiply instead of y:

   run PE_PE matrix_multiply = run PE (PE, matrix_multiply)
   

   As established above:

   run PE (PE, matrix_multiply) = PE_matrix_multiply
   

   where the specialized program PE_matrix_multiply is a program specializer that is dedicated to specializing the matrix-multiplication program.

   So we conclude that PE_PE maps matrix_multiply to a program specializer that is dedicated to specializing matrix_multiply:

   run PE_PE matrix_multiply = PE_matrix_multiply
   

1. A simpler argument.

   This case reads:

   run PE_PE matrix_multiply = result
   

   which is an instance of the third characteristic equation:

    run PE (p, x) = p_x
   run PE (PE, p) = PE_p
       run PE_p x = p_x
   

   with

   • PE for p and
   • matrix_multiply for x

   and where we are asked to describe what p_x denotes.

   Substituting PE for p and matrix_multiply for x, the third characteristic equation reads:

   run PE_PE matrix_multiply = PE_matrix_multiply
   

   As elaborated above, PE_matrix_multiply is a program specializer that is dedicated to specializing the matrix-multiplication program.

   So we conclude that PE_PE maps matrix_multiply to a program specializer that is dedicated to specializing matrix_multiply.

2. This case reads:

   run PE_PE GP = result
   

   which is an instance of the third characteristic equation:

    run p (x, y) = result
   run PE (p, x) = p_x
       run p_x y = result
   

   with

   • PE for p,
   • PE for x, and
   • GP for y

   and where we are asked to describe what result denotes.

   Quoting the above:

   The specialized program PE_p is a program specializer that is dedicated to specializing p. And indeed running p_x on y gives the same result as running p on both x and y:

   run p_x y  = run p (x, y)
   

   Let us instantiate this quote with PE instead of p, PE instead of x, and GP instead of y:

   run PE_PE GP = run PE (PE, GP)
   

   As established above:

   run PE (PE, GP) = PE_GP
   

   where the specialized program PE_GP is a program specializer that is dedicated to specializing the general parser.

   So we conclude that PE_PE maps GP to a program specializer that is dedicated to specializing GP:

   run PE_PE GP = PE_GP
   

2. A simpler argument.

   This case reads:

   run PE_PE GP = result
   

   which is an instance of the third characteristic equation:

    run PE (p, x) = p_x
   run PE (PE, p) = PE_p
       run PE_p x = p_x
   

   with

   • PE for p and
   • GP for x

   and where we are asked to describe what p_x denotes.

   Substituting PE for p and GP for x, the third characteristic equation reads:

   run PE_PE GP = PE_GP
   

   As elaborated above, PE_GP is a program specializer that is dedicated to specializing the general parser.

   So we conclude that PE_PE maps GP to a program specializer that is dedicated to specializing GP.

3. This case reads:

   run PE_PE unparse = result
   

   It is an instance of the third characteristic equation:

    run p (x, y) = result
   run PE (p, x) = p_x
       run p_x y = result
   

   with

   • PE for p,
   • PE for x, and
   • unparse for y

   and where we are asked to describe what result denotes.

   Quoting the above:

   The specialized program PE_p is a program specializer that is dedicated to specializing p. And indeed running p_x on y gives the same result as running p on both x and y:

   run p_x y  = run p (x, y)
   

   Let us instantiate this quote with PE instead of p, PE instead of x, and unparse instead of y:

   run PE_PE unparse = run PE (PE, unparse)
   

   As established above:

   run PE (PE, unparse) = PE_unparse
   

   where the specialized program PE_unparse is a program specializer that is dedicated to specializing the unparser.

   So we conclude that PE_PE maps unparse to a program specializer that is dedicated to specializing unparse:

   run PE_PE unparse = PE_unparse
   

3. A simpler argument.

   This case reads:

   run PE_PE unparse = result
   

   which is an instance of the third characteristic equation:

    run PE (p, x) = p_x
   run PE (PE, p) = PE_p
       run PE_p x = p_x
   

   with

   • PE for p and
   • unparse for x

   and where we are asked to describe what p_x denotes.

   Substituting PE for p and unparse for x, the third characteristic equation reads:

   run PE_PE unparse = PE_unparse
   

   As elaborated above, PE_unparse is a program specializer that is dedicated to specializing the unparser.

   So we conclude that PE_PE maps unparse to a program specializer that is dedicated to specializing unparse.

Postlude

Loki: A partial solution about a partial evaluator. I see.

Mimer: Harrumph.

Version

Added the concrete example of the program with 3 inputs [29 Jan 2021]

Added the meaning of a program in the section about Programs and the function they compute, the cookbook example in the section about Kleene’s S-m-n function, the section about I-diagrams, revisited, the section about Program equivalence, and the food for thought about a diagrammatical rendition of PE [28 Jan 2021]

Added Pinocchio and Cyrano’s interventions in the interlude, the simpler argument in the partial solution for Exercise 7, and the postlude [25 Jan 2021]

Fixed a typo in the partial solution for Exercise 7 [24 Jan 2021]

Discarded the recurrent food and re-hauled the narrative using instances of the characteristic equations [24 Jan 2021]

Added the recurrent food for thought and the hint towards solving Exercise 2 [24 Jan 2021]

Fixed a typo about PE_GP and PE_unparse, thanks to Sewen Thy’s eagle eye [24 Jan 2021]

Added the S-m-n characteristic equations about S-0-n and S-m-0, following Aaditya Patwari’s request for clarification [24 Jan 2021]

Fixed a typo about P being a parser dedicated to g, thanks to Aaditya Patwari’s eagle eye [24 Jan 2021]

Created [21 Jan 2021]