Towards OCaml

• So languages are characterized by grammars.

• Regarding the three linguistic layers of characters, words, and sentences:

  • the legal characters are typically enumerated (e.g., letters, digits, punctuation marks, etc.), along with which ones are separators;
  • legal words are sequences of characters, as per the lexical structure of the language; and
  • legal sentences are sequences of words, as per the grammatical structure of the language.

  While this layering is descriptive in a natural language, it is prescriptive in a programming language.

• In emacs, typing M-x run-ocaml starts a read-eval-print loop (also known as a toplevel loop) where one types an OCaml expression, punctuated by ;; and the Enter key; the systems then reads this expression. Then, to a first approximation:

  • if this expression is grammatically incorrect, an error message is displayed and the read-eval-print loop is resumed;
  • if this expression is grammatically correct, it is evaluated:
    • if this evaluation yields an error, an error message is displayed and the read-eval-print loop is resumed;
    • if this evaluation requires more time resources than we have (e.g., because it is silently diverging), nothing happens until we type C-c C-c (i.e., simultaneously press the control key (as one would press the shift key) and the key c, twice); an error message is then displayed and the read-eval-print loop is resumed;
    • if this evaluation requires more space resources than what is available in our computer, an error message is displayed and the read-eval-print loop is resumed; and
    • if this evaluation completes with a result, this result is displayed and the read-eval-print loop will be resumed.

  Typing C-c C-d stops OCaml.

• OCaml is a language of expressions.

• Through the toplevel loop, these expressions are evaluated and yield values. These values have a type: integer, boolean, string, etc.

  This notion of type is not only specific to values: it characterizes the expressions that gave rise to these values. These expressions have the type of the value they evaluate to.

  Furthermore, this notion of type is not only specific to OCaml expressions: it characterizes the OCaml programming language itself, in that its syntactic constructs are typed as well. This characterization has significant consequences:

  • To be concrete, consider a compiler from OCaml to, e.g., x86 written, e.g., in x86. Using this compiler to execute an OCaml program proceeds in two steps: (1, compile time) the program is compiled, and (2, run time) the compiled program is executed. What happens at compile time is traditionally said to be static and what happens at run time is traditionally said to be dynamic. So for example, parsing (i.e., the verification that the given program is syntactically correct) happens at compile time, and the execution of a (syntactically correct) program happens at run time: parsing happens statically. In OCaml, typing (i.e., the verification that the given program is type correct) also happens at compile time, and the execution of a (type-correct) program happens at run time: typing happens statically.

    Well-typed programs cannot go wrong.

    —Robin Milner

  • As such, OCaml is a statically typed programming language: only expressions that are syntactically correct and that are type-correct too are evaluated. All the other expressions (i.e., the syntactically incorrect expressions and the syntactically correct but type-incorrect expressions) are rejected. The benefit of this syntactic discipline is that running an OCaml program never gives rise to a syntax error since only grammatically correct expressions are evaluated. The benefit of this typing discipline is that running an OCaml program never gives rise to a type error since only type-correct expressions are evaluated.

  Type systems have been developed “bottom up”, i.e., as increased abstractions of desired computational behaviors. So it is something of a surprise that they also have a logical content, but this topic is out of scope here.

Binary relations – a reminder

To quote the Wikipedia entry about binary relations, in mathematics, a binary relation over two sets A and B is a set of ordered pairs (a, b) consisting of elements a in A and b in B.

For example, the relation “is greater than” over the set of integers Z is the set of pairs of integers (i, j) for which there exists a positive integer k such that i = j + k. This particular relation is often represented using a set comprehension: {(i, j) | i belongs to the set of integers Z, j belongs to Z, and there exists a positive integer k such that i = j + k}.

Mathematical functions – a reminder

To quote the Wikipedia entry about functions, in mathematics, a function is a relation between two sets – the domain of the function and its codomain – that maps each element of the domain to at most one element of the codomain.

Examples (of functions):

• The “successor” function over the set of integers Z is the relation {(i, j) | i + 1 = j}. Here, both the domain and the codomain of the successor function are Z.
• The “absolute value” function maps a negative integer -i to the natural number i and a non-negative integer i to the natural number i. Here, the domain is Z (the set of integers) and the codomain is N (the set of natural numbers).

A function is often represented with its graph in that the pairs in its relation are the Cartesian coordinates of points in the Euclidean plane, a geometric rendition of the enumeration of these pairs. For example, the successor function over natural numbers is enumerated with {(0, 1), (1, 2), (2, 3), ...} and the square function over natural numbers with {(0, 0), (1, 1), (2, 4), (3, 9), ...}.

A predicate is a function whose codomain is the set of Booleans.

Examples (of predicates):

• A function that maps any negative integer to false and any non-negative integer to true.
• A function that maps any even integer to true and any odd integer to false.

Total functions – a reminder

A function is total when it maps each element of its domain to one element of its codomain. The successor function over natural numbers, for example, is total.

Partial functions – a reminder

A function is partial when it does not map each element of its domain to an element of its codomain. The predecessor function over natural numbers, for example, is partial because while it maps any natural number n+1 to n, it does not map 0 to any natural number. For another example, a function over integers that is only defined over non-negative integers is also partial.

Equivalence of functions / functional equality

Two functions are equivalent when they have the same graph.

Consider two functions f and g from N (the set of natural numbers) to B (the set of Booleans):

f : N -> B

g : N -> B

Comparing two natural numbers for equality is carried out using the infix operator =_N (the equality sign indexed with N) and comparing two Booleans for equality is carried out using the infix operator =_B (the equality sign indexed with B). (And these operators are said to be “infix” because they occur between their two operands, like addition (+), subtraction (-), etc.)

Equivalently to the graph characterization above, f and g are equivalent (or: functionally equal) if they map equal natural numbers to equal booleans:

for any natural numbers i and j
and
for any Booleans x and y such that f(i) = x and g(j) = y
if i =_N j then x =_B y

Or again, equivalently:

for any natural numbers i and j
and
for any Booleans x and y such that f(i) = x and g(j) = y
  x =_B y whenever i =_N j

More concisely:

for any natural number i,
  f(i) =_B g(i)

This all suggests the notation =_(N -> B), the equality sign indexed with N -> B, for an infix operator to compare two functions:

f =_(N -> B) g whenever for any natural numbers i and j,
                          f(i) =_B g(i) whenever i =_N j

We will revisit this indexed notation when unparsing OCaml values.

Functions in Computer Science

• Macroscopically, a program (say, p) processes data and computes a function (say, f, so that run p = f) that maps input information (represented by input data) to output information (represented by output data):

  

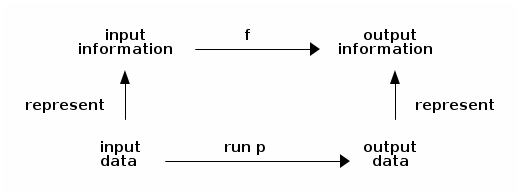
  The processing is carried out by a program that computes a function.

• Microscopically, we can implement functions in OCaml. (What we call “an OCaml function”, however, is not a mathematical function.)

Program equivalence, revisited

Two programs are equivalent when the functions they compute are equivalent, i.e., if either running them on the same input yields the same output or if, ran on the same input, they both diverge.

Program equivalence is undecidable in general because of the halting problem: we cannot decide whether running a program (here: two programs) halts or diverges.

Postlude

Harald: The diagram about functions and the programs that compute these functions is becoming more and more precise.

Alfrothul: But it could be even more precise.

Harald: Even more precise?

Alfrothul: Suppose that the input and the output data don’t have the same type.

Harald: Right, that can happen. For example, the function the program computes could map a natural number to a Boolean.

Alfrothul: So we should look at this “represent” arrow a bit more closely.

Brynja: How about we use a pair of functions instead?

Harald: Now what.

Alfrothul: No, no, that makes sense, we need some bi-directionality here between information and data.

Brynja: We could call one “encode”, to encode information into data, and the other one “decode”, to decode data into information.

Harald (suspicious): What about the types?

Brynja: Right. We could define a family of such functions, with each one indexed by a type. We would use them to encode numbers and to decode representations of numbers, to encode Booleans and to decode representations of Booleans, etc.

Vigfus (prompt): Aha, so the diagram would look actually like this:

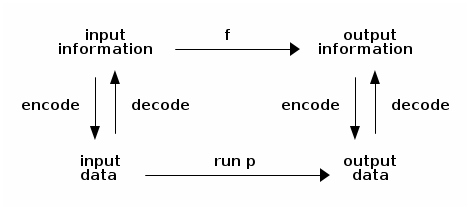
Alfrothul: And now we can see clearly that given some encoded input information, the program produces some output data that can be decoded into output information:

f (input_information) = decode (run p (encode input_information))

Harald: Actually, the converse holds just as well. The function maps some decoded input data into some output information that can be encoded into output data:

encode (f (decode input_data)) = run p input_data

Brynja: Depending which path in the diagram you want to take. Of course this all assumes that the two paths are equivalent, which they should be if the encoding/decoding functions and the program are correct.

Mimer: This kind of diagram is known as a “commuting” diagram.

Loki: Mimer, you sound quite categorical here.

Mimer (repressing a smile): Another such commuting diagram relates the interpreter for a source language, a compiler from this source language to a target language, and the interpreter for this target language:

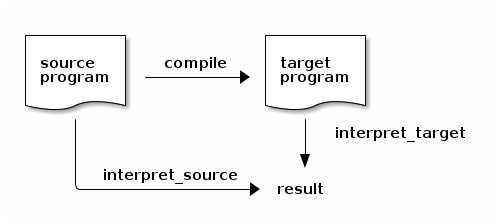
Brynja: I see. For any source_program:

run interpret_source source_program = run interpret_target (run compile source_program)

Harald: But what if there is a syntax error in source_program?

Brynja: Well, I guess the source interpreter and the compiler both should detect it and report it, preferably in the same manner. After all, they both parse their input.

Alfrothul: And what if there is a semantic error in source_program, that is to say, what if executing source_program raises an error?

Brynja: Well, I guess the source interpreter and the target interpreter should report it too, preferably in the same manner.

Mimer: You guys are going to have so much fun in the term project.

Version

Added the postlude [02 Feb 2021]

Added the diagram and the bits about functional equality and program equivalence [02 Feb 2021]

Created [30 Jan 2021]