Mini-project: A study of right-to-left linked lists

Here is the type of polymorphic right-to-left lists (hereby: “tsils”):

type 'a tsil = Lin | Snoc of 'a tsil * 'a;;

Halcyon: On behalf of all the left-handed people in the world, thank you.

For example,

• evaluating Snoc (Lin, 0) gives rise to the following construct, where Lin is depicted with ][ and Snoc with a box with two entries:

  

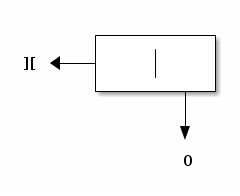
• evaluating Snoc (Snoc (Lin, 0), 1) gives rise to the following construct:

  

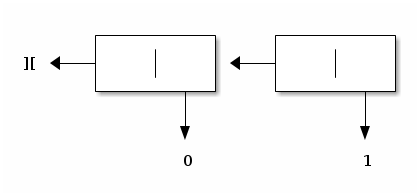
• evaluating Snoc (Snoc (Snoc (Lin, 0), 1), 2) gives rise to the following construct:

  

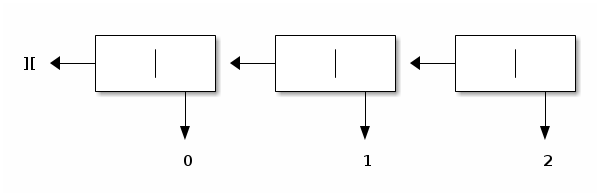
1. Specify and implement a tsil_length function that computes the length of a tsil in the same manner as List.length computes the length of a list.

2. Specify and implement a tsil_append function that computes the concatenation of two tsils in the same manner as List.append computes the concatenation of two lists, as per the description of list concatenation in Week 08.

   Pictorially, concatenating, e.g.,

   

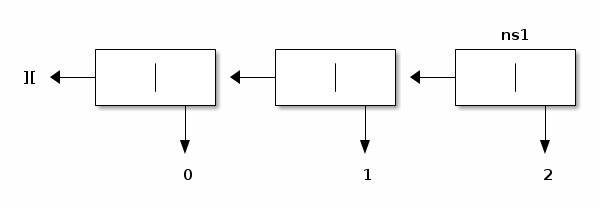
   (naming this tsil ns1) and, e.g.,

   

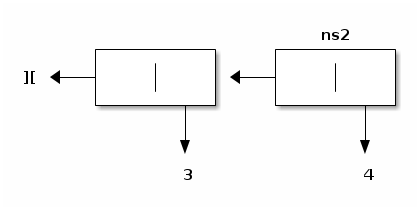
   (naming this tsil ns2) should yield

   

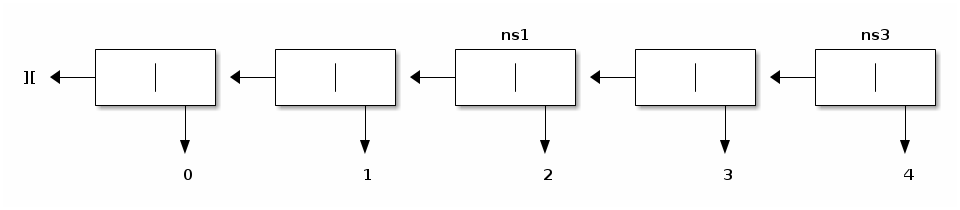
   (naming this tsil ns3).

3. Specify and implement a tsil_map function that maps a function to each of the elements of a tsil and construct the tsil of the results, in the same manner as list_map maps a function to each of the elements of a list and constructs the corresponding list with the results.

4. Implement two versions of a tsil_reverse function that reverses a tsil: one without an accumulator that uses tsil_append, and one with an accumulator that only uses Snoc.

5. Specify and implement two conversion functions tsil_of_list and list_of_tsil that convert lists to tsils and vice versa:

   let test_tsil_of_list candidate =
     let b0 = (candidate [] = Lin)
     and b2 = (candidate (1 :: 0 :: []) = Snoc (Snoc (Lin, 0), 1))
     (* etc. *)
     in b0 && b2;;
   
   let test_list_of_tsil candidate =
     let b0 = (candidate Lin = [])
     and b2 = (candidate (Snoc (Snoc (Lin, 0), 1)) = 1 :: 0 :: [])
     (* etc. *)
     in b0 && b2;;
   

6. Using tsil_of_list and list_of_tsil, implement

   • tsil_length in terms of list_length,
   • list_length in terms of tsil_length,
   • tsil_map in terms of list_map, and
   • list_map in terms of tsil_map.

7. Time permitting, implement the tsil counterparts of list_fold_right and of list_fold_left.

Prelude

Anton: A prelude at the end of a mini-project, now.

Dana: Unless this ‘lude is meant to be read before embarking on this mini-project?

Alfrothul (meditative): That could well be, you know. That could just well be.

Dana: Well, along the same line, and since time is short, I think we should start this mini-project with its last question.

Anton (O_o): Its last question.

Dana: Well, yes – start by implementing tsil_of_list and list_of_tsil.

Alfrothul: Why?

Dana: Well, because tsils are the right-to-left analogue of lists – and vice versa – and therefore it only makes sense that what a function does on lists, its analogue should do on tsils, and vice versa too. Look:

let tsil_transformer_of_list_transformer f =
 (* tsil_transformer_of_list_transformer : ('a list -> 'b list) -> 'a tsil -> 'b tsil *)
  fun sv -> tsil_of_list (f (list_of_tsil sv));;

let list_transformer_of_tsil_transformer g =
 (* list_transformer_of_tsil_transformer : ('a tsil -> 'b tsil) -> 'a list -> 'b list *)
  fun vs -> list_of_tsil (g (tsil_of_list vs));;

Anton: Oh. You mean that tsil_reverse should do the analogue of List.rev, for example?

Dana: Sure do:

# tsil_transformer_of_list_transformer List.rev (Snoc (Snoc (Snoc (Lin, 3), 2), 1));;
- : int tsil = Snoc (Snoc (Snoc (Lin, 1), 2), 3)
#

Anton: I see – applying the tsil analogue of the reverse function to the tsil analogue of a list yields the tsil analogue of the reverse of this list.

Halcyon (cringing): Headache!

Pablito (beaming): This is so convenient for writing our unit tests.

Alfrothul: Actually, the same idea works for functions that produce lists or tsils:

let tsil_producer_of_list_producer f =
 (* tsil_producer_of_list_producer : ('a -> 'b list) -> 'a -> 'b tsil *)
  fun v -> tsil_of_list (f v);;

let list_producer_of_tsil_producer f =
 (* list_producer_of_tsil_producer : ('a -> 'b tsil) -> 'a -> 'b list *)
  fun v -> list_of_tsil (f v);;

Dana: Yup. Applying tsil_producer_of_list_producer to atoi, for example, yields a function that maps a non-negative integer to the tsil of its successive predecessors.

Anton: Ditto for functions that take lists as input, and tsils too:

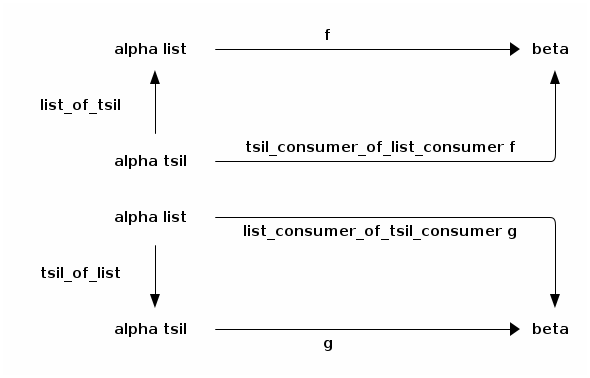
let tsil_consumer_of_list_consumer f =
 (* tsil_consumer_of_list_consumer : ('a list -> 'b) -> 'a tsil -> 'b *)
 fun sv -> f (list_of_tsil sv);;

let list_consumer_of_tsil_consumer g =
 (* list_consumer_of_tsil_consumer : ('a tsil -> 'b) -> 'a list -> 'b *)
  fun vs -> g (tsil_of_list vs);;

Pablito: You were right, this prelude should be read before embarking on this mini-project.

Halcyon: Well, my headache didn’t go away.

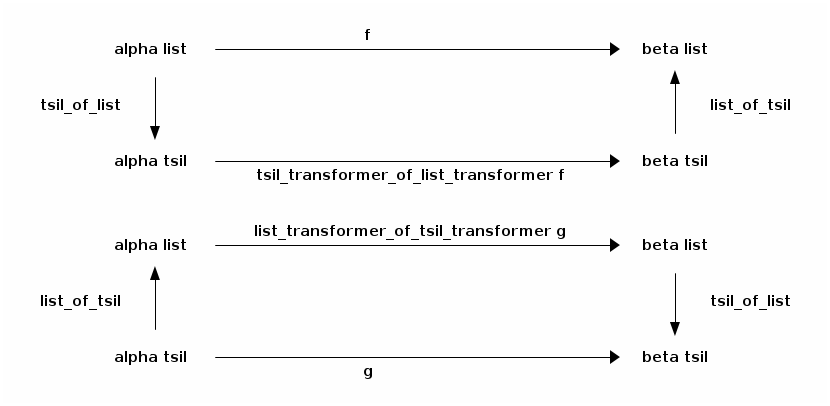
Dana: Commuting diagrams to the rescue. First, tsil_transformer_of_list_transformer and list_transformer_of_tsil_transformer:

Alfrothul: Then, tsil_producer_of_list_producer and list_producer_of_tsil_producer:

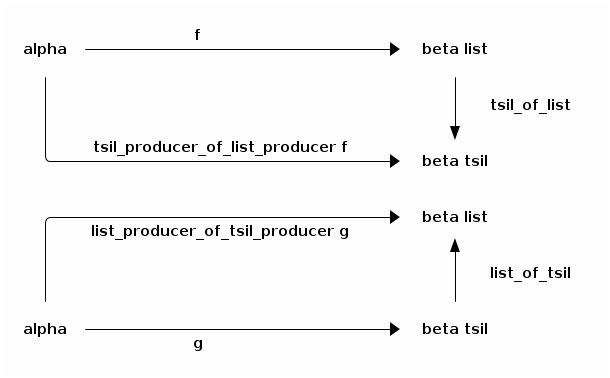
Anton: And then, tsil_consumer_of_list_consumer and list_consumer_of_tsil_consumer:

Resources

• The OCaml code for the present lecture note (latest version: 27 Oct 2022).

Version

Created [27 Oct 2022]