Background and general introduction

With the exception of recursion,

all the concepts in these lecture notes are presented in Aristotelian order,

progressing from known things towards unknown things.

There are no hidden forward references, and no rabbits are pulled out of hats,

a questionable strategy that is known to make hats proliferate at a Fibonacci rate.

—Mimer

Computer Science, Computing Science, Data Science, and Informatics

The term “Computer Science” comes from American English. In this term, the emphasis is on the computer, from its architecture all the way to its use. However, as Turing award Edsger Dijkstra allegedly put it once in The Netherlands, Computer Science is no more [only] about computers than astronomy is [only] about telescopes. And so often, the term “Computing Science” is used instead, where the emphasis is on the processing of data on computers. For Turing award Peter Naur in Denmark, the emphasis should be on the representation of information as data on computers for processing, and so he proposed the terms “datalogi” and “Data Science” instead. For Karl Steinbuch in Germany and for Philippe Dreyfus in France, the emphasis should be on the automated treatment of information by processing data on computers, and so they proposed “Informatik” in 1956 and “informatique” in 1962, terms that are rendered in English as “informatics”.

To sum up, data are representations of information in a computer, and these representations are processed to carry out a computation. And while the term “Computer Science” is the accepted one, alternative terms exist. For example,

• the National University of Singapore has a School of Computing and the University of Oxford had a Computing Laboratory,
• the University of Edinburgh has a School of Informatics and the Technical University of Denmark has a Department of Informatics,
• Acta Informatica and Fundamenta Informaticae are two peer-reviewed journals in theoretical computer science,
• the “C” in “ACM” stands for “Computing”,
• the “D” in “DIKU”, at the University of Copenhagen, stands for “Datalogi”,
• the closing “I” and “A” in “INRIA” respectively stand for “Informatique” and (translated into English:) “Automation”, and
• the “C” in the MCS major at Yale-NUS College stands for “Computation” (the contender was “Environmental Studies” for three years running).

Information and data

Data represent information:

Data are built using data constructors:

• A representation is sound when using constructors correctly always yields a piece of data that correctly represents the information it is meant to represent. (Otherwise this representation is unsound.)
• A representation is complete when all the information we wish to represent can be represented using the data constructors. (Otherwise this representation is incomplete.)

For example, in OCaml (the programming language of discourse for Intro to CS), the default representation of integers has a fixed size, and so only integers between, e.g., -4611686018427387904 and 4611686018427387903 can be represented. This representation is sound in that the representation of any integer between -4611686018427387904 and 4611686018427387903 does correspond to a mathematical integer, but it is incomplete since integers smaller than -4611686018427387904 or greater than 4611686018427387903 cannot be represented.

For another example, in Chez Scheme, the default representation of integers does not have a fixed size: this representation is complete... up to the size of the memory of our computer.

Exercise 02

1. Install Chez Scheme, an implementation of the Scheme programming language where expressions are fully parenthesized and operations are prefixed.

2. Start Chez Scheme from an Emacs terminal (M-x shell):

   Chez Scheme Version 9.5.1
   Copyright 1984-2017 Cisco Systems, Inc.
   
   >
   

3. Compute successive exponents of 2 by evaluating (expt 2 0), (expt 2 1), (expt 2 2), (expt 2 3), (expt 2 10), (expt 2 100), (expt 2 1000), (expt 2 10000), etc.:

   > (expt 2 0)
   1
   > (expt 2 1)
   2
   > (expt 2 2)
   4
   > (expt 2 3)
   8
   > (expt 2 10)
   1024
   > (expt 2 100)
   1267650600228229401496703205376
   > (expt 2 200)
   1606938044258990275541962092341162602522202993782792835301376
   > (expt 2 300)
   2037035976334486086268445688409378161051468393665936250636140449354381299763336706183397376
   > (expt 2 500)
   ...
   > (expt 2 1000)
   ...
   >
   

4. Keep increasing the exponent until the result is too big to fit in the screen.

5. Go back to the beginning of the buffer (ESC <), resize Emacs’s fonts (C-x - and then C-x - - - -), and contemplate the exponential growth of these successive integers.

6. Resize Emacs’s fonts back to normal (C-x + 0), go to the end of the buffer (ESC >), and visualize several exponentiations not of 2, but of 10:

   > (expt 10 0)
   ...
   > (expt 10 1)
   ...
   > (expt 10 2)
   ...
   > (expt 10 3)
   ...
   > (expt 10 10)
   ...
   > (expt 10 100)
   ...
   >
   

   Briefly analyze these successive results.

7. Food for thought:

   If Chez Scheme were printing integers in base 2 instead of in base 10, what would be the result of evaluating (expt 2 0), (expt 2 1), (expt 2 2), (expt 2 3), etc.?

   N.B.: As it happens, the ~b option of the resident string-formatting procedure format provides this conversion in base 2:

   > (format "~b" (expt 2 0))
   ...
   > (format "~b" (expt 2 1))
   ...
   > (format "~b" (expt 2 2))
   ...
   > (format "~b" (expt 2 3))
   ...
   >
   

Exercise 03

What is the smallest power of 2 that is larger than the number of minutes since your birth?

Solution for Exercise 03

Anton: That sounds doable.

Alfrothul: Yes. Assuming the reader is 20 years old, that’s the number of years since their birth.

Anton: Right. And multiplying this number by 12 gives the number of months since their birth:

> (* 20 12)
240
>

Alfrothul: Multiplying this number by 30 roughly gives the number of days since their birth:

> (* 20 12 30)
7200
>

Dana: A bit less roughly, there is 365 days in one year.

Alfrothul: Thanks:

> (* 20 365)
7300
>

Anton: Multiplying this number by 24 gives the number of hours since their birth:

> (* 20 365 24)
175200
>

Alfrothul: And multiplying this number by 60 gives the number of minutes since their birth:

> (* 20 365 24 60)
10512000
>

Anton: As for a power of 2, how about 25:

> (expt 2 25)
33554432
>

Alfrothul: Too big. Perhaps 23:

> (expt 2 23)
8388608
>

Anton: Too small. So 24:

> (expt 2 24)
16777216
>

Alfrothul: Let me check:

> (and (< (expt 2 23) (* 20 365 24 60)) (< (* 20 365 24 60) (expt 2 24)))
#t
>

Anton: Right. Between 2 to the power of 23 and 2 to the power of 24.

Alfrothul: OK.

Pablito (sorro voce): Prefixed and fully parenthesized, eh.

Dana: And never mind the leap years.

Alfrothul: Well, they occur every four years, and we assumed the reader to be 20 years old.

The fourth wall: Coming through, please.

Some vocabulary

A “digit” is a number in the representation of an integer. For example, the integer 123 contains 3 digits, and the one on the left is not 0. This integer is implicitly expressed in base 10, and it represents the polynomial 1 * 10^2 + 2 * 10^1 + 3 * 10^0. Each coefficient in a 10-based polynomial lies between 0 and 9. So a digit is a coefficient in the polynomial representation of an integer and an integer is represented as the concatenation of these digits.

In base 2, a number is represented with the concatenation of the coefficients of the corresponding 2-based polynomial. For example, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, etc. are represented as 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, etc. So 1001 in base 2 represents 1 * 2^3 + 0 * 2^2 + 0 * 2^1 + 1 * 2^0, i.e., 9 in base 10. Each coefficient in a 2-based polynomial lies between 0 and 1. A “bit” is a coefficient in a 2-based polynomial.

Exercise 04

1. Given a positive integer, what is the relation between this integer and the number of its digits?
2. Consider a positive integer written in base 2. What is the relation between this integer and the number of its digits?

Epistemology of representation

In a nutshell, a representation and what this representation represents are two distinct things:

• a name is not what it denotes (e.g., we are not our name);
• the address of one’s home is not one’s home;
• a musical note is not its name (e.g., because musical notes have several names: do, ré, mi, fa, sol, etc. or A, B, C, D, etc.);
• etc.

Interlude

Anton: So a number is not its name?

Mimer: Right. A number is not its name.

Anton: So much for the multiplication tables.

Mimer (surprised): The multiplication tables?

Anton: Yes. We had to learn them by heart.

Halcyon (nostalgic): We were singing them too.

Mimer: Well, the multiplication tables are still valid any way we look at them.

Anton: Yes, but suddenly they are less simple.

Mimer: Why? They also work in another language than the one you grew up with.

Anton: Harrumph.

Epistemology of representation (continued)

So a name and what this name denotes are two distinct things.

Several of René Magritte‘s paintings illustrate this point, e.g., The Treachery of Images where the painting of a pipe is accompanied by the words “Ceci n’est pas une pipe” (“This is not a pipe”), a point that Walter Jon Williams developed eloquently in his novel This is not a game and that Kira Kutscher illustrated tellingly in the following painting since sometimes, one cause is enough:

Kira Kutscher (thoughtfully): Still, this is not a definition.

Mimer: Ms. Kutscher! Thanks for coming by! And thanks for the painting too!

Computing as data processing

A computer processes data. Given some input data that represent input information, it can:

• produce output data that represent output information,
• issue an error message (which is also a piece of output data), or
• loop, i.e., not produce any output data.

A “batch” computation is carried out by representing input information as input data and processing this input data in a way that produces output data that represents output information:

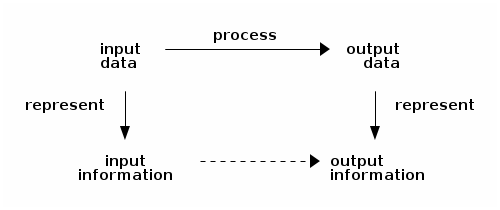
There are of course other forms of computations than batch ones, e.g., reactive ones that process events (e.g., a key being pressed on a keyboard or the movement of a mouse) as these events occur, but batch computations are a good starting point:

• Assuming that processing the input data d1 yields the output data d2, then if d1 represents a piece of information i1 and d2 represents a piece of information i2, then the batch computation is said to be sound if we wanted to map i1 to i2.
• Assuming we want to map a piece of information i1 to a piece of information i2, then if i1 is represented by d1 and i2 is represented by d2, then this batch computation is said to be complete if processing d1 yields d2.

Interlude

Bong-sun: Let’s see. In the RGB color model, the red, green, and blue primary colors are combined together to produce other colors.

Dana: Yes. By its very nature, this model is sound because every RGB triplet corresponds to a color.

Alfrothul: And it is not complete because not every color can be represented as a RGB triplet.

Pablito: Computing here yields new RGB triplets: it has a chance to be sound because every RGB triplet corresponds to a color.

Halcyon: And it cannot be complete because not every color can be represented as a RGB triplet.

Programs

A program is the recipe the computer follows to process data: a program that processes input data into output data computes a function from input information to output information. A program is written by a programmer.

Here is a comparison. A cooking recipe is a notation that conveys how to cook something. It specifies data (the ingredients, e.g., eggs, butter, salt, pepper, thyme), resources and tools (e.g., a stove and a pan), and an algorithm (a method to operate on the data, e.g., to beat the eggs towards cooking an omelet). To make a dish, a cook uses the kitchen resources and tools to operate over the ingredients according to the algorithm.

Exercise 05

The goal of this exercise is to pursue the analogy between programs and cooking recipes.

• The data are the ingredients.
• The computer at large is the kitchen.
• The processor, in the computer, is the cook in the kitchen.
• The program is the cooking recipe.

What is the cooking analogue of a programmer?

Exercise 06

The goal of this exercise is to establish an analogy between computing and knitting.

• The data are the yarns.
• The computer at large is the work environment of the person who is knitting, including, e.g., knitting needles.
• The processor, in the computer, is the person who is knitting.

What is the knitting analogue of a program?

What is the knitting analogue of a programmer?

Exercise 07

The goal of this exercise is to establish an analogy between computing and making music.

• The data are the sounds.
• The computer at large is anything that can make a sound.

What is the musical analogue of the processor, in the computer?

What is the musical analogue of a program (improvisation notwithstanding)?

What is the musical analogue of a programmer?

Programming languages

A programming language is the language in which a program is written: a notation to express computations. There are many notions of computation (i.e., ways of representing information and ways of processing data), and for each of these notions, there are many notations (i.e., many programming languages).

What we need are notions, not notations.

—Carl-Friedrich Gauss (quoted by Paul Lockhart in his Mathematician’s Lament)

What’s in a name?

Amusingly, the four names Computer Science, Computing Science, Data Science, and Informatics correspond to Aristotle’s four causes:

• Data Science (material cause):

  As put forward by Peter Naur, the topic here is centered on data that represent information.

• Computing Science (efficient cause):

  The topic here is centered on data processing, i.e., computing.

• Computer Science (formal cause):

  The topic here is the methodology of computing, i.e., how to carry out computations.

• Informatics (final cause):

  As put forward by Karl Steinbuch and Philippe Dreyfus, the topic here is the automated treatment of information.

Computer Science by any other name is about being perceptive and thinking logically and reflectively.

Data Science in the 21st century

Nowadays, technological progress made it possible for data to be so large that they need to be handled using statistical tools, and so the term “Data Science” has taken a new meaning. This meaning is captured in the following humorous riddle, heard while attending a workshop at the NUS Department of Statistics and Data Science in 2019:

Question: What is the difference between a data scientist and a statistician?

Answer: A data scientist is a useful statistician.

(One simply has to admire people who don’t take themselves seriously while taking their job most seriously.)

Postlude

Loki: It would indeed be nonsensical to refer to Astronomy as “Telescope Science”.

Mimer: Glad you agree.

Loki: Instead, it should be referred to as “Telescoping Science”.

Mimer (who didn’t see this one coming): Telescoping Science.

Loki (warming up): Or better, on the ground that Computer Science is about data (cf. Data Science), Astronomy should be called Star Science, based on its etymology. As for the Big Bang, ...

Mimer (hastily): You know what, Loki, you are right. And by that logic, top astronomers would be nominated to the Star Academy. It would make so much more science, I mean sense.

Loki: Glad you agree. Next step: meteorology, the science of meteors.

Halcyon (to himself): Another invitation for critical reading, methinks.

Credit

The RGB example was suggested by Avery Snow.

Version

Added the interlude about the RGB color model [30 Jan 2024]

Refined the narrative about soundness and completeness in Section Computing as data processing [30 Jan 2024]

Added a pointer to the definition of the term “implementation” in Exercise 02 [21 Jan 2023]

Created [10 Jan 2023]