Towards OCaml

• So languages are characterized by grammars.

• Regarding the three linguistic layers of characters, words, and sentences:

  • legal characters are typically letters, digits, punctuation marks, etc., and some of these characters are “separators”;
  • legal words are sequences of characters (delimited by separators, e.g., the space character), as per the lexical structure of the language; and
  • legal sentences are sequences of words, as per the grammatical structure of the language.

  While this layering is descriptive in a natural language, it is prescriptive in a programming language: any sequence of characters that is not lexically correct and grammatically correct is rejected.

• In Emacs, typing M-x run-ocaml starts a read-eval-print loop (also known as a toplevel loop) where one is presented with a prompt, #. One then types an OCaml expression, punctuated by ;; and hits the Enter key. The system reads this expression, and then, to a first approximation:

  • if this expression is lexically or grammatically incorrect, an error message is displayed and the read-eval-print loop is resumed;
  • if this expression is lexically and grammatically correct, it is evaluated:
    • if this evaluation yields an error, an error message is displayed and the read-eval-print loop is resumed;
    • if this evaluation requires more time resources than we have (e.g., because it is silently diverging), nothing happens until we type C-c C-c (i.e., simultaneously press the control key (as one would press the shift key) and the key c, twice); an error message is then displayed and the read-eval-print loop is resumed;
    • if this evaluation requires more space resources than what is available in our computer, an error message is displayed and the read-eval-print loop is resumed; and
    • if this evaluation completes with a result, this result is displayed and the read-eval-print loop is resumed.

  Typing either #quit;; or C-c C-d stops OCaml.

• OCaml is a language of expressions.

• Through the toplevel loop, OCaml expressions are evaluated and yield values. These values have a type: integer, boolean, string, etc.

  This notion of type is not only specific to values: it characterizes the expressions that gave rise to these values. These expressions have the type of the value they evaluate to.

  Furthermore, this notion of type is not only specific to OCaml expressions: it characterizes the OCaml programming language itself, in that its syntactic constructs are typed as well. This characterization has significant consequences:

  • To be concrete, consider a compiler from OCaml to, e.g., x86 written, e.g., in x86. Using this compiler to execute an OCaml program proceeds in two steps: (1, compile time) the program is compiled, and (2, run time) the compiled program is executed. What happens at compile time is traditionally said to be static and what happens at run time is traditionally said to be dynamic. So for example, parsing (i.e., the verification that the given program is syntactically correct) happens at compile time, and the execution of a (syntactically correct) program happens at run time: parsing happens statically. In OCaml, typing (i.e., the verification that the given program is type correct) also happens at compile time, and the execution of a (type-correct) program happens at run time: typing happens statically.

    Well-typed programs cannot go wrong.

    —Robin Milner

  • As such, OCaml is a statically typed programming language: only expressions that are syntactically correct and that are type-correct too (i.e., that do not add apples and oranges) are evaluated. All the other expressions (i.e., the syntactically incorrect expressions and the syntactically correct but type-incorrect expressions) are rejected. The benefit of this syntactic discipline is that running an OCaml program never gives rise to a syntax error since only grammatically correct expressions are evaluated. The benefit of this typing discipline is that running an OCaml program never gives rise to a type error since only type-correct expressions are evaluated.

  • In contrast, programming languages such as Lisp (Emacs is programmed in Lisp) and Scheme are dynamically typed in that running a Lisp and a Scheme program can give rise to type errors.

  Type systems have been developed “bottom up”, i.e., as increased abstractions of desired computational behaviors. So it is something of a surprise that they also have a logical content (as in: mathematical logic), but this topic is out of scope here.

An analogy about dynamic vs. static types

Imagine an open laboratory (“lab” for short) where each door is locked. There, each lab member carries a set of keys with them, and wherever they need to go, they use one of their keys. And so only authorized people (i.e., people with a key) can go through doors.

Now imagine a closed laboratory whose entry is restricted to lab members. There, doors have no locks and lab members carry no keys.

• An open lab is dynamically typed in that every time someone wants to go through a door, an access test takes place to check whether this person is authorized to go through this door, i.e., has its key.
• A closed lab is statically typed in that only authorized personnel is admitted in it, and so lab members can freely go through doors since their access test already took place when they entered the premises.

Likewise, consider a computation that consists in a series of operations, where each operation consists of applying an operator to operands:

• if the computation was specified in a dynamically typed programming language, before each operation, the types of its operands are verified to be compatible with the type of its operator; and
• if the computation was specified in a statically typed programming language, each operation takes place straight away because the types of its operands have already been verified to be compatible with the type of its operator before the computation started.

Binary relations – a reminder

To quote the Wikipedia entry about binary relations, in mathematics, a binary relation over two sets A and B is a set of ordered pairs (a, b) consisting of elements a in A and b in B.

For example, the relation “is greater than” over the set of integers Z is the set of pairs of integers (i, j) for which there exists a positive integer k such that i = j + k. This particular relation is often represented using a set comprehension: {(i, j) | i belongs to the set of integers Z, j belongs to Z, and there exists a positive integer k such that i = j + k}.

For another example, consider the relation “represents” over a data set D and an information set I. This relation is sound if for all d in D, there exists an i in I such that (i, d) is in the relation, and it is complete if for all i in I, there exists a d in D such that (i, d) is in the relation.

Mathematical functions – a reminder

To quote the Wikipedia entry about functions, in mathematics, a function is a relation between two sets – the domain of the function and its codomain – that maps each element of the domain to at most one element of the codomain.

Examples (of functions):

• The “successor” function over the set of integers Z is the relation {(i, j) | i + 1 = j}. Here, both the domain and the codomain of the successor function are Z.
• The “absolute value” function maps a negative integer -i to the natural number i and a non-negative integer i to the natural number i. Here, the domain is Z (the set of integers) and the codomain is N (the set of natural numbers).

A function is often represented with its graph in that the pairs in its relation are the Cartesian coordinates of points in the Euclidean plane, a geometric rendition of the enumeration of these pairs. For example, the successor function over natural numbers is enumerated with {(0, 1), (1, 2), (2, 3), ...} and the square function over natural numbers with {(0, 0), (1, 1), (2, 4), (3, 9), ...}.

A predicate is a function whose codomain is the set of Booleans.

Examples (of predicates):

• A function that maps any negative integer to false and any non-negative integer to true.
• A function that maps any even integer to true and any odd integer to false.

Total functions – a reminder

A function is total when it maps each element of its domain to one element of its codomain. The successor function over natural numbers, for example, is total.

Partial functions – a reminder

A function is partial when it does not map each element of its domain to an element of its codomain. The predecessor function over natural numbers, for example, is partial because while it maps any natural number n+1 to n, it does not map 0 to any natural number. For another example, a function over integers that is only defined over non-negative integers is also partial.

Equivalence of functions / functional equality

Two functions are equivalent when they have the same graph.

Consider two functions f and g from N (the set of natural numbers) to B (the set of Booleans):

f : N -> B

g : N -> B

Comparing two natural numbers for equality is carried out using the infix operator =_N (the equality sign indexed with N) and comparing two Booleans for equality is carried out using the infix operator =_B (the equality sign indexed with B). (And these operators are said to be “infix” because they occur between their two operands, like addition (+), subtraction (-), etc.)

Equivalently to the graph characterization above, f and g are equivalent (or: functionally equal) if they map equal natural numbers to equal booleans:

for any natural numbers i and j
and
for any Booleans x and y such that f(i) = x and g(j) = y
if i =_N j then x =_B y

Or again, equivalently:

for any natural numbers i and j
and
for any Booleans x and y such that f(i) = x and g(j) = y
  x =_B y whenever i =_N j

More concisely:

for any natural number i,
  f(i) =_B g(i)

This all suggests the notation =_(N -> B), the equality sign indexed with N -> B, for an infix operator to compare two functions:

f =_(N -> B) g whenever for any natural numbers i and j,
                          f(i) =_B g(i) whenever i =_N j

We will revisit this indexed notation when unparsing OCaml values.

Functions in Computer Science

• Extensionally, a program (say, p) processes data and computes a function (say, f, so that run p = f) that maps input information (represented by input data) to output information (represented by output data):

  

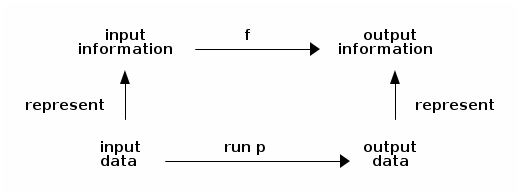
  The processing is carried out by a program that computes a function.

• Intensionally, we can implement functions in OCaml. (What we call “an OCaml function”, however, is not a mathematical function.)

Program equivalence, revisited

Two programs are equivalent when the functions they compute are equivalent, i.e., if either running them on the same input elicits the same observable effects and either yields the same output or diverges. (The notion of observable effects is developed in Week 04.)

Program equivalence is undecidable in general because of the halting problem: we cannot decide whether running a program (here: two programs) halts or diverges.

Postlude

Anton: The diagram about functions and the programs that compute these functions is becoming more and more precise.

Alfrothul: But it could be even more precise.

Anton: Even more precise?

Alfrothul: Suppose that the input and the output data don’t have the same type.

Anton: Right, that can happen. For example, the function the program computes could map a natural number to a Boolean.

Alfrothul: So we should look at this “represent” arrow a bit more closely.

Dana: How about we use a pair of functions instead?

Anton: Now what.

Alfrothul: No, no, that makes sense, we need some bi-directionality here between information and data.

Dana: We could call one “encode”, to encode information into data, and the other one “decode”, to decode data into information:

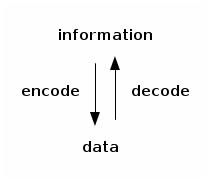
Pablito: So information is encoded as data and data are decoded as information?

Alfrothul: Yup. Data represent information whenever they can be decoded as such.

Pablito (thoughtfully): What about soundness and completeness?

Mimer: Good point, Pablito. The representation is sound and complete when encode and decode are inverses of each other:

decode (encode information) = information

encode (decode data) = data

Anton (suspicious): What about the types?

Dana: Right. We could define a family of such functions, with each one indexed by a type. We would use them to encode numbers and to decode representations of numbers, to encode Booleans and to decode representations of Booleans, etc.

Pablito (prompt): Aha, so the diagram would look actually like this:

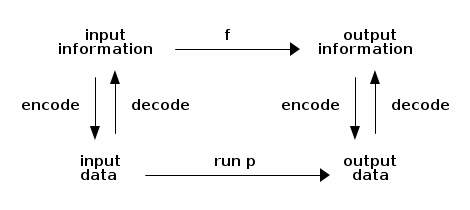
Alfrothul: And now we can see clearly that given some encoded input information, the program produces some output data that can be decoded into output information:

f (input_information) = decode (run p (encode input_information))

Anton: Actually, the converse holds just as well. The function maps some decoded input data into some output information that can be encoded into output data:

encode (f (decode input_data)) = run p input_data

Dana: Depending which path in the diagram you want to take. Of course this all assumes that the two paths are equivalent, which they should be if the encoding/decoding functions and the program are sound and complete, i.e., correct.

Mimer: This kind of diagram is known as a “commuting” diagram.

Loki: Mimer, you sound quite categorical here.

Mimer (repressing a smile): Another such commuting diagram relates the interpreter for a source language, a compiler from this source language to a target language, and the interpreter for this target language:

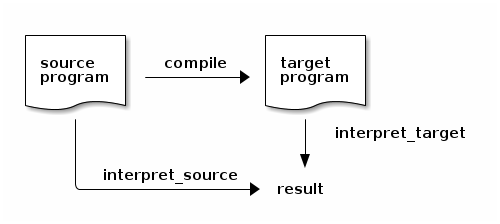
Dana: I see. For any source_program:

run interpret_source source_program = run interpret_target (run compile source_program)

Anton: But what if there is a syntax error in source_program?

Dana: Well, I guess the source interpreter and the compiler both should detect it and report it, preferably in the same manner. After all, they both parse their input.

Alfrothul: And what if there is a semantic error in source_program, that is to say, what if executing source_program raises an error?

Dana: Well, I guess the source interpreter and the target interpreter should report it too, preferably in the same manner.

Mimer: You guys are going to have so much fun in the mini-project about arithmetic expressions.

Exercise 01

The goal of this exercise is to revisit the commuting diagram for batch computations:

As pointed out above, this diagram can be rendered algebraically with two equations:

f (input_information) = decode (run p (encode input_information))

encode (f (decode input_data)) = run p input_data

State two more equations that render this commuting diagram.

In a nutshell

Data—the representation of information—is often partitioned depending on the type of information we want to represent: integers, booleans, characters, strings, pairs, functions, arrays, etc. Trying to add apples and oranges while executing a program is known as a type error. The notion of type can be lifted from run time (dynamic types) to compile time (static types) in that they are not just a property of data but a property of the program that processes these data. Furthermore this notion of static type can be lifted from each individual program to the programming language in which this program is written. OCaml, for example, is a statically typed programming language in that it is specified not just with a grammar but with typing rules and so to be valid, a program must not only be grammatically correct but type correct too. The genius in this design is that the typing rules are designed in such a way that if a program has a type, then executing it does not give rise to a type error, an achievement due to founding fathers of Computer Science such as Gordon D. Plotkin and Robin Milner, to whom we owe ML and therefore OCaml. Also, types in programming languages turn out to have a logical content in that their structure is isomorphic to the structure of propositions in mathematical logic, which is awesome.

Credit

The example of the “represents” relation is due to Avery Snow.

Version

Fine-tuned the revisitation of program equivalence [29 Jan 2023]

Added the analogy about dynamic vs. static types [27 Jan 2023]

Polished the narrative some more and added Exercise 01 [23 Jan 2023]

Created [26 Aug 2022]