Reversing lists

The goal of this lecture note is to describe how to reverse lists and the ensuing programming pattern of using accumulators.

Resources

• The OCaml code for the present lecture note (latest version: 26 Mar 2023).

Reversing a list

Reversing a list means listing its elements in reverse order:

let test_list_reverse_int candidate =
  let b0 = (candidate [] = [])
  and b1 = (candidate [0] = [0])
  and b2 = (candidate [1; 0] = [0; 1])
  and b3 = (candidate [2; 1; 0] = [0; 1; 2])
  (* etc. *)
  in b0 && b1 && b2 && b3;;

Besides, list reversal is obviously involutory, i.e., applying it twice in a row to a list yields back this list. More ammunition for our unit-test function:

let test_list_reverse_int candidate =
  let b0 = (candidate [] = [])
  and b1 = (candidate [0] = [0])
  and b2 = (candidate [1; 0] = [0; 1])
  and b3 = (candidate [2; 1; 0] = [0; 1; 2])
  and b4 = (let ns = atoi 100
            in candidate (candidate ns) = ns)
  (* etc. *)
  in b0 && b1 && b2 && b3 && b4;;

OCaml offers a predefined function, List.rev, that does the job:

# test_list_reverse_int List.rev;;
- : bool = true
#

Writing a function list_reverse that, given a list, returns its converse requires some thought, however. Indeed OCaml lists are constructed by starting from the empty list, and successively adding elements in front of the list that has been constructed so far. Take the list [2; 1; 0], for example, as constructed by atoi. It is a traditional linked list with one forward link and no back link. Pictorially:

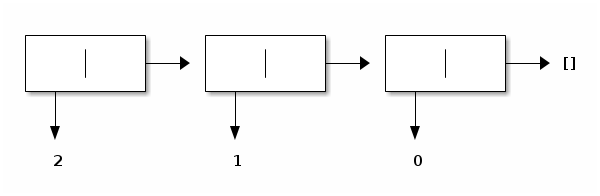
This list is constructed starting from the empty list, by adding 0 in front, and then by adding 1 in front, and then by adding 2 in front:

# [];;
- : 'a list = []
# 0 :: [];;
- : int list = [0]
# 1 :: 0 :: [];;
- : int list = [1; 0]
# 2 :: 1 :: 0 :: [];;
- : int list = [2; 1; 0]
#

Symmetrically, its converse is [0; 1; 2]. It is constructed starting from the empty list, by adding 2 in front, and then by adding 1 in front, and then by adding 0 in front:

# [];;
- : 'a list = []
# 2 :: [];;
- : int list = [2]
# 1 :: 2 :: [];;
- : int list = [1; 2]
# 0 :: 1 :: 2 :: [];;
- : int list = [0; 1; 2]
#

Pictorially:

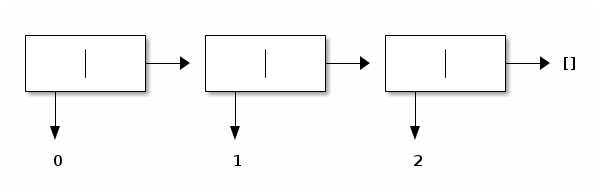
The challenge for writing a function list_reverse lies in the very nature of the one list constructor and the two list accessors: List.cons, List.hd, and List.tl all operate at the beginning of a list. However, the elements at the beginning of the input list occur at the end of the output list, and vice versa.

Reversing a list, Version 1: the first shall be the last

Fortunately, a modicum of recursive thinking solves the problem:

• reversing the empty list yields the empty list; and

• reversing a nonempty list will require combining its head with the result of reversing its tail (which is the induction hypothesis).

  Let us revisit the example of the list [2; 1; 0]. Its head is 2 and its tail is [1; 0]. Reversing its tail yields [0; 1]. Our problem is as follows: given 2 and [0; 1], how do we obtain [0; 1; 2]? The List.append function springs to the mind: we could apply it to [0; 1] and to ...? And to ...? It can’t be to 2 since List.append expects both of its parameters to be lists. So let us make a singleton list out of 2 (i.e., a list that only contains one element) and apply List.append to [0; 1] and to this singleton list, [2]: the result is [0; 1; 2], as desired.

In OCaml:

let list_reverse_v1 vs_given =
  let rec visit vs =
    if vs = []
    then []
    else let v = List.hd vs
         and vs' = List.tl vs
         in let ih = visit vs'
            in List.append ih [v]
  in visit vs_given;;

Let us run it through the unit test:

# test_list_reverse_int list_reverse_v1;;
- : bool = true
#

Success.

Food for thought:

• Consider the successive calls to visit in list_reverse_v1 and visualize them when this visit function (printed as list_reverse_v1 below) is applied to the list [2; 1; 0]:

  # traced_list_reverse_v1 show_int [2; 1; 0];;
  list_reverse_v1 [2; 1; 0] ->
    visit_list_reverse_v1 [2; 1; 0] ->
      visit_list_reverse_v1 [1; 0] ->
        visit_list_reverse_v1 [0] ->
          visit_list_reverse_v1 [] ->
          visit_list_reverse_v1 [] <- []
        visit_list_reverse_v1 [0] <- [0]
      visit_list_reverse_v1 [1; 0] <- [0; 1]
    visit_list_reverse_v1 [2; 1; 0] <- [0; 1; 2]
  list_reverse_v1 [2; 1; 0] <- [0; 1; 2]
  - : int list = [0; 1; 2]
  #
  

  See how, at call time, visit_list_reverse_v1 is applied to the successive suffixes of [2; 1; 0] and how, at return time, it returns the successive prefixes of [0; 1; 2]?

• Both the time and space complexity of List.hd and List.tl are constant. Both the time complexity and the space complexity of List.append are linear on its first argument, since List.append prepends its first argument (i.e., copies it) in front of its second argument. Here is the same computation as above, but this time with traced versions of List.hd, List.tl, and List.append:

  # supertraced_list_reverse_v1 show_int [2; 1; 0];;
  list_reverse_v1 [2; 1; 0] ->
    visit_list_reverse_v1 [2; 1; 0] ->
      list_hd [2; 1; 0] <-> 2
      list_tl [2; 1; 0] <-> [1; 0]
      visit_list_reverse_v1 [1; 0] ->
        list_hd [1; 0] <-> 1
        list_tl [1; 0] <-> [0]
        visit_list_reverse_v1 [0] ->
          list_hd [0] <-> 0
          list_tl [0] <-> []
          visit_list_reverse_v1 [] ->
          visit_list_reverse_v1 [] <- []
        list_append [] [0] ->
          visit_list_append [] ->
          visit_list_append [] <- [0]
        list_append [] [0] <- [0]
        visit_list_reverse_v1 [0] <- [0]
      list_append [0] [1] ->
        visit_list_append [0] ->
          visit_list_append [] ->
          visit_list_append [] <- [1]
        visit_list_append [0] <- [0; 1]
      list_append [0] [1] <- [0; 1]
      visit_list_reverse_v1 [1; 0] <- [0; 1]
    list_append [0; 1] [2] ->
      visit_list_append [0; 1] ->
        visit_list_append [1] ->
          visit_list_append [] ->
          visit_list_append [] <- [2]
        visit_list_append [1] <- [1; 2]
      visit_list_append [0; 1] <- [0; 1; 2]
    list_append [0; 1] [2] <- [0; 1; 2]
    visit_list_reverse_v1 [2; 1; 0] <- [0; 1; 2]
  list_reverse_v1 [2; 1; 0] <- [0; 1; 2]
  - : int list = [0; 1; 2]
  #
  

  Therefore, at return time, the successive prefixes of the given list are copied, which corresponds to allocating 0 + 1 + 2 + ... + n pairs if the given list has length n+1, or again n * (n + 1) / 2, a number that is proportional to the square of n.

  So both the time complexity and the space complexity of list_reverse_v1 are quadratic. That doesn’t feel right because the size of the output is the same as the size of the input. Shouldn’t the complexity of reversing a list be linear (i.e., proportional to the length of this list) rather than quadratic (i.e., proportional to the square of this length)?

Reversing a list, Version 2: the last shall be the first

Just as plausibly, however, we could assume two functions list_hd_op and list_tl_op that are converses of List.hd and List.tl.

• Whereas applying List.hd to a nonempty list returns the first element of that list, applying list_hd_op to a nonempty list would return its last element:

  let test_list_hd_op_int candidate =
    let b0 = (0 = candidate [0])
    and b1 = (0 = candidate [1; 0])
    and b2 = (0 = candidate [2; 1; 0])
    and b3 = (0 = candidate [5; 4; 3; 2; 1; 0])
    (* etc. *)
    in b0 && b1 && b2 && b3;;
  

  Given a nonempty list, list_hd_op traverses it in search of its last element and returns it:

  let list_hd_op vs_given =
    match vs_given with
    | [] ->
       let () = Printf.printf "list_hd_op: invalid argument" in
       assert false
    | v :: vs' ->
       let rec visit v vs =
         match vs with
         | [] ->
            v
         | v' :: vs' ->
            visit v' vs'
       in visit v vs';;
  

  As a sanity check, let us run it through its unit tests:

  # test_list_hd_op_int list_hd_op;;
  - : bool = true
  #
  

  The accompanying resource file contains a traced version of list_hd_op to visualize its operations:

  # supertraced_list_hd_op show_char [];;
  list_hd_op [] ->
  list_hd_op: invalid argument
  Exception: Assert_failure ("week-09_list-reversal.ml", 284, 8).
  # supertraced_list_hd_op show_char ['1'; '2'; '3'; '4'; '5'];;
  list_hd_op ['1'; '2'; '3'; '4'; '5'] ->
    visit_list_hd_op '1' ['2'; '3'; '4'; '5'] ->
    visit_list_hd_op '2' ['3'; '4'; '5'] ->
    visit_list_hd_op '3' ['4'; '5'] ->
    visit_list_hd_op '4' ['5'] ->
    visit_list_hd_op '5' [] ->
    visit_list_hd_op '1' ['2'; '3'; '4'; '5'] <- '5'
  list_hd_op ['1'; '2'; '3'; '4'; '5'] <- '5'
  - : char = '5'
  

  In words:

  • If list_hd_op is applied to an empty list, an error message is issued, assert false is evaluated, and the computation is discontinued.
  • If list_hd_op is applied to a nonempty list, here '1' :: ['2'; '3'; '4'; '5'], then visit is applied to '1' and ['2'; '3'; '4'; '5']. This list is traversed tail-recursively until it ends, and then visit returns its first argument, i.e., '5' in the present example: '5' is the last element of the given list.

• Whereas applying List.tl to a nonempty list returns [the list of] all the elements of that list except the first (i.e., its longest strict suffix), applying list_tl_op to a nonempty list would return [the list of] all the elements of that list, except the last (i.e., its longest strict prefix):

  let test_tl_op_int candidate =
    let b0 = (candidate [0] = [])
    and b1 = (candidate [1; 0] = [1])
    and b2 = (candidate [2; 1; 0] = [2; 1])
    and b3 = (candidate [5; 4; 3; 2; 1; 0] = [5; 4; 3; 2; 1])
    (* etc. *)
    in b0 && b1 && b2 && b3;;
  

  Given a nonempty list, list_tl_op copies it in the same order up to and excluding the last element and returns the resulting first strict prefix:

  let list_tl_op vs_given =
    match vs_given with
    | [] ->
       let () = Printf.printf "list_tl_op: invalid argument\n" in
       assert false
    | v :: vs' ->
       let rec visit v vs =
         match vs with
         | [] ->
            []
         | v' :: vs' ->
            let ih = visit v' vs'
            in v :: ih
       in visit v vs';;
  

  As a sanity check, let us run it through its unit tests:

  # test_list_tl_op_int list_tl_op;;
  - : bool = true
  #
  

  The accompanying resource file also contains a traced version list_tl_op to visualize its operations:

  # supertraced_list_tl_op show_int [];;
  list_tl_op [] ->
  list_tl_op: invalid argument
  Exception: Assert_failure ("//toplevel//", 58, 8).
  # supertraced_list_tl_op show_int [1; 2; 3; 4; 5];;
  list_tl_op [1; 2; 3; 4; 5] ->
    visit_list_tl_op 1 [2; 3; 4; 5] ->
      visit_list_tl_op 2 [3; 4; 5] ->
        visit_list_tl_op 3 [4; 5] ->
          visit_list_tl_op 4 [5] ->
            visit_list_tl_op 5 [] ->
            visit_list_tl_op 5 [] <- []
          visit_list_tl_op 4 [5] <- [4]
        visit_list_tl_op 3 [4; 5] <- [3; 4]
      visit_list_tl_op 2 [3; 4; 5] <- [2; 3; 4]
    visit_list_tl_op 1 [2; 3; 4; 5] <- [1; 2; 3; 4]
  list_tl_op [1; 2; 3; 4; 5] <- [1; 2; 3; 4]
  - : int list = [1; 2; 3; 4]
  #
  

  In words:

  • If list_tl_op is applied to an empty list, an error message is issued, assert false is evaluated, and the computation is discontinued.
  • If list_tl_op is applied to a nonempty list, here 1 :: [2; 3; 4; 5], then visit is applied to 1 and [2; 3; 4; 5]. This list is traversed recursively until it ends, and then visit returns the empty list and all the previous recursive calls to visit construct a new result by “consing” their first argument to the result of the previous recursive call. The result is the list that contains all the elements of the given list except the last one, in the same order.

  Pictorially,

  • the given list is represented as follows:

    

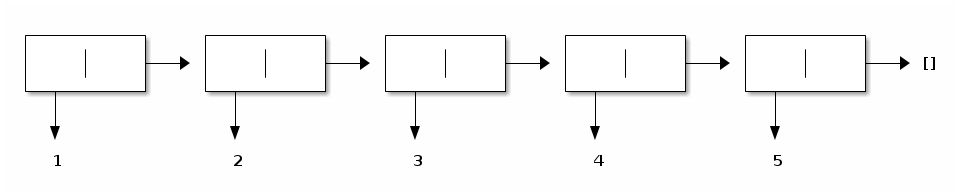
  • and the returned list is represented as follows:

    

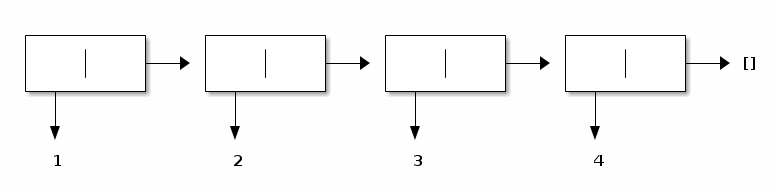
    The returned list was constructed afresh: a (nonempty) list and a (nonempty) prefix of this list share no pairs since lists are linked from left to right (unlike a nonempty list and a nonempty suffix of this list, as seen in Week 08).

Using list_hd_op and list_tl_op, writing list_reverse is straightforwardly done using structural recursion. In the induction step, to reverse a nonempty list, we cons its last element to the result of reversing its first strict suffix:

let list_reverse_v2 vs_given =
  let rec visit vs =
    if vs = []
    then []
    else list_hd_op vs :: visit (list_tl_op vs)
  in visit vs_given;;

Let us run it through the unit tests:

# test_list_reverse_int list_reverse_v2;;
- : bool = true
#

Success.

Food for thought:

• What would list_reverse_v2 compute if list_hd_op were replaced by List.hd and list_tl_op by List.tl?

• Consider the successive calls to visit in list_reverse_v2 and visualize them when list_reverse_v2 is applied, e.g., to the list [2; 1; 0].

  See how, at call time, visit is applied to the successive prefixes of [2; 1; 0] and how, at return time, visit returns the successive suffixes of [0; 1; 2]?

• Both the time and space complexity of List.cons are constant. The time complexity of list_hd_op is linear on its argument, and its space complexity is constant. Both the time complexity and the space complexity of list_tl_op are linear on its argument.

  Therefore, both at call time and at return time, visit incurs a cost that is linearly proportional to the length of its argument. If the input of list_reverse_v2 has length n+1, the overall cost of using visit is linearly proportional to n + (n-1) + ... + 2 + 1 + 0, or again n * (n + 1) / 2, a number that is proportional to the square of n.

  So both the time complexity and the space complexity of list_reverse_v2 are quadratic. Again, that doesn’t feel right because the size of the output is the same as the size of the input. Again, shouldn’t the complexity of reversing a list be linear rather than quadratic?

Reversing a list, Version 3: trading space for time

Common to Versions 1 and 2 of list_reverse is the successive copying of all the elements but the last one either of the input list (Version 2, with list_tl_op) or of the result of the recursive calls (Version 1, with List.append). We could trade space for time with an index, using List.nth to pick the successive elements of the list in reverse order:

let list_reverse_v3 vs =
  let rec visit i =
    if i = 0
    then []
    else let i' = pred i
         in let ih = visit i'
            in (List.nth vs i') :: ih
  in visit (list_length vs);;

This version passes the unit tests:

# test_list_reverse_int list_reverse_v3;;
- : bool = true
#

Food for thought:

• Consider the successive calls to visit in list_reverse_v3 and visualize them when list_reverse_v3 is applied to the list [2; 1; 0].

  See how, at call time, the argument of visit decreases all the way to 0 and how, at return time, visit returns the successive suffixes of [0; 1; 2]?

• In contrast to the two first versions, this version only uses List.cons to construct the result, and since the complexity of List.cons is constant, the space complexity of list_reverse_v3 is linear. (Yay.)

• Still, for a list of length n, list_reverse_v3

  • traverses the list with n tail calls to compute its length;
  • traverses the list with n-1 tail calls to access its nth element;
  • traverses the list with n-2 tail calls to access its (n-1)th element;
  • ...
  • traverses the list with 2 tail calls to access its 3rd element;
  • traverses the list with 1 tail call to access its 2nd element; and
  • traverses the list with 0 tail calls to access its 1st element.

  All in all, given a list of length n, list_reverse_v3 makes n + n-1 + n-2 + ... + 2 + 1 + 0 tail calls, i.e., its time complexity is quadratic.

  So while the space complexity of list_reverse_v3 is linear, its time complexity is quadratic. That still doesn’t feel right because why should we need a quadratic time complexity to perform a computation whose space complexity is linear?

Reversing a list, Version 4: using an accumulator

We have not been thinking right about list reversal:

• the first element of the input list is the first element that will be consed [to the empty list] to construct the result;
• the second element of the input list is the second element that will be consed to construct the result;
• the third element of the input list is the third element that will be consed to construct the result;
• etc.

We should exploit this coincidence by synchronizing the traversal of the input list and the construction of the output list. To this end, let us add a second argument to the local function that traverses the input list and let us accumulate the output list over this second argument during the traversal:

let list_reverse_v4 vs_given =
  let rec visit vs a =
    if vs = []
    then a
    else let v = List.hd vs
         and vs' = List.tl vs
         in visit vs' (v :: a)
  in visit vs_given [];;

Or again, using a match-expression, as one positively and definitely should do in practice:

let list_reverse_v5 vs_given =
  let rec visit vs a =
    match vs with
    | [] ->
       a
    | v :: vs' ->
       visit vs' (v :: a)
  in visit vs_given [];;

Both versions pass the unit test:

# test_reverse reverse_v4;;
- : bool = true
# test_reverse reverse_v5;;
- : bool = true
#

Food for thought:

• Consider the successive calls to visit in list_reverse_v4 and visualize them when list_reverse_v4 is applied, e.g., to the list [1; 2; 3; 4; 5]:

  # traced_list_reverse_v4 show_int [1; 2; 3; 4; 5];;
  list_reverse_v4 [1; 2; 3; 4; 5] ->
    visit_list_reverse_v4 [1; 2; 3; 4; 5] [] ->
    visit_list_reverse_v4 [2; 3; 4; 5] [1] ->
    visit_list_reverse_v4 [3; 4; 5] [2; 1] ->
    visit_list_reverse_v4 [4; 5] [3; 2; 1] ->
    visit_list_reverse_v4 [5] [4; 3; 2; 1] ->
    visit_list_reverse_v4 [] [5; 4; 3; 2; 1] ->
  list_reverse_v4 [1; 2; 3; 4; 5] <- [5; 4; 3; 2; 1]
  - : int list = [5; 4; 3; 2; 1]
  #
  

  • Observe how all calls to visit are tail calls and therefore visit only returns once? This version is iterative: it implements a loop.
  • Observe the synchronicity, at call time, between incrementally traversing the input and constructing the output.
  • Observe the loop invariants (i.e., properties) in the successive tail-calls to visit:
    • the first actual parameter enumerates the successive suffixes of the given list (denoted by vs_given), from this given list all the way to the empty list;
    • the second actual parameter enumerates the successive reversed prefixes of the given list, from the empty list all the way to the final result;
    • at every call, concatenating the reverse of the second actual parameter and the first actual parameter yields the given list;
    • at every call, concatenating the reverse of the first actual parameter and the second actual parameter yields the resulting list.

• In contrast to the three first versions, this version only uses List.cons, List.hd, and List.tl, whose time complexity and space complexity are constant. Therefore both the time complexity and space complexity of reverse_v4 are linear.

The extra argument for visit is called an accumulator, and as it happens, it is not only useful to reverse a list – far from it, as developed in the next lecture note.

Exercise 01

Summarize the key points of the sections above (Versions 1 to 4). What are the pros and cons of each of the successive list-reverse functions?

Exercise 02

Given the standard definitions of List.append (to concatenate two lists), List.rev (to reverse a list), and List.map (to map a function over a list, homomorphically), consider the following 10 functions:

0. fun xs ys -> List.append (List.rev xs) (List.rev ys)
1. fun xs ys -> List.append (List.rev ys) (List.rev xs)
2. fun xs ys -> List.rev (List.append ys xs)
3. fun xs ys -> List.rev (List.append xs ys)
4. fun f xs -> List.map f (List.rev xs) assuming that f will always denote a pure and total function
5. fun f xs -> List.rev (List.map f (List.rev xs)) assuming that f will always denote a pure and total function
6. fun f xs -> List.rev (List.map f xs) assuming that f will always denote a pure and total function
7. fun f xs -> List.map f xs assuming that f will always denote a pure and total function
8. fun f xs ys -> List.map f (List.append xs ys) assuming that f will always denote a pure and total function
9. fun f xs ys -> List.append (List.map f xs) (List.map f ys) assuming that f will always denote a pure and total function

In reference to Exercise 10 in Week 08, which of these functions are equivalent? Briefly justify each answer, e.g., by drawing commuting diagrams, possibly using the following swap arrow:

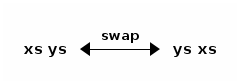
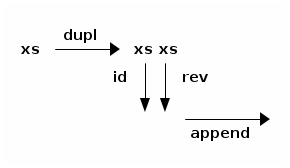
For example, also assuming a duplication arrow (dupl) and an identity arrow (id), the following diagram captures how to map a list into a palindrome of even length:

Subsidiary question, assuming that String.append denotes a string-concatenation function and String.rev denotes a string-reversal function:

• If we were to replace List. with String. in the functions above, would your answers be the same? Why?

Exercise 03

The following OCaml function maps a given function over the elements of a given list and returns the reversed list of the results:

let list_pam f vs =
  List.rev (List.map f vs);;

Implement a recursive OCaml function that does the same but without creating an intermediate list.

‘lude

Pablito: So the following implementation doesn’t cut it:

let list_pam_alt f vs =
  List.map f (List.rev vs);;

Mimer: Right.

Pablito: But it computes the same.

Mimer: If you say so.

Pablito: Hmmm...

Mimer: Yes?

Pablito: Let me go back to Exercise 02.

Exercise 04

The following OCaml function, when applied to 2 lists, prepends the reverse of the first list to the second list:

let list_rev_append v1s v2s =
  List.append (List.rev v1s) v2s;;

Implement a recursive OCaml function that does the same but without creating an intermediate list.

Resources

• The OCaml code for the present lecture note (latest version: 26 Mar 2023).

Version

Expanded the resource file with a template for Exercise 02, Exercise 03, and Exercise 04 [26 Mar 2023]

Created [13 Oct 2022]