Pairs, binary trees, and lists

See also

The Scheme Programming Language

by R. Kent Dybvig

Goal

This chapter introduces Scheme pairs and how they are used to construct binary trees and lists.

Resources

• The Scheme code for the present lecture note (latest version: 07 Sep 2025).

Pairs

The predefined procedure cons takes two arguments and returns a pair that groups these two arguments. The associated type predicate is pair? and the two pair accessors are car and cdr:

> (pair? 32)
#f
> (pair? (cons 10 20))
#t
> (car (cons 10 20))
10
> (cdr (cons 10 20))
20
> (cdr (car (cons (cons 10 20) 30)))
20
>

In general, pairs are printed with parentheses and a dot in the middle:

> (cons 10 20)
(10 . 20)
> (cons (cons 10 20) 30)
((10 . 20) . 30)
>

Pictorially:

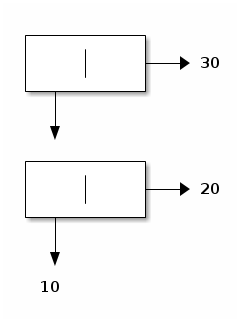
By convention, for pairs whose cdr is another pair, the dot and the subsequent parentheses are omitted:

> (cons 10 (cons 20 30))
(10 20 . 30)
>

Pictorially:

The challenge with pairs

In Scheme, pairs are mutable, i.e., their components can be changed.

The predefined procedure set-car! (resp. set-cdr!), when applied to a pair and to a Scheme value, modifies the first (resp. the second) component of the given pair with the given value:

> (define p (cons 1 10))
> p
(1 . 10)
> (set-car! p 2)
> p
(2 . 10)
> (set-cdr! p 20)
> p
(2 . 20)
>

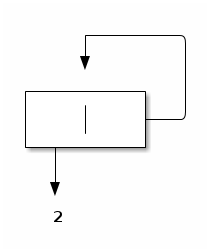
It is therefore very simple to construct cyclic values, i.e., values that refer to themselves:

> (set-cdr! p p)
> p

Warning in pretty-print: cycle detected; proceeding with (print-graph #t)
#0=(2 . #0#)
>

(In Chez Scheme’s read-eval-print loop, values are printed using Chez Scheme’s pretty-print procedure, which detects cycles.)

Pictorially:

Warning

Values that are constructed with cons – e.g., binary trees and lists later in this chapter – need to be processed with caution because they might be cyclic.

Bong-sun: So if we are given a value and we want to traverse it recursively...

Mimer: ...we should be wary that it might be cyclic, yes.

Bong-sun: Harrumph.

Alfrothul: What Bong-sun said.

Binary trees

Pairs make it possible to construct the nodes of a binary tree. For example, here is a BNF of binary trees within Scheme values:

<binary-tree>      ::= <binary-tree_leaf>
                     | <binary-tree_node>

<binary-tree_leaf> ::= ...any Scheme value but a pair...

<binary-tree_node> ::= (<binary-tree> . <binary-tree>)

A sample of binary trees of integers

Here is how to construct five binary trees of integers:

1. a binary tree that consists of a leaf:

   (define t0_int
     0)
   

2. a binary tree that consists of one node and two leaves:

   (define t1
     (cons 1 10))
   

3. two binary trees that contain two nodes and three leaves:

   (define t2
     (cons 1 (cons 10 100)))
   
   (define t3
     (cons (cons 1 -10) 100))
   

4. one binary tree that consists of three nodes and four leaves:

   (define t4
     (cons (cons 1 10) (cons 100 1000)))
   

On the occasion, it is a good idea to systematically indent the constructors in these definitions, to emphasize the correspondence between the meaning of the resulting construction (the semantics) and the form of how they were constructed (the syntax). For example,

• here is the definition of t4, re-indented:

  (define t4
    (cons (cons 1
                10)
          (cons 100
                1000)))
  

• here is a graphical depiction of what t4 denotes:

  

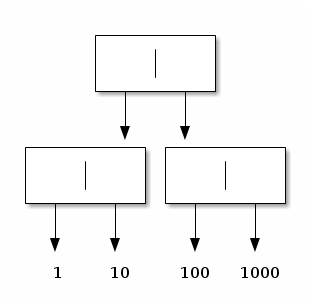
These two layouts make it clear that

• the binary tree denoted by t4 has four leaves that contain the integers 1, 10, 100, and 1000,

• this binary tree has three nodes,

• the least integer contained in its leaves is 1, in the left subtree of its left subtree,

• the largest integer contained in its leaves is 1000, in the right subtree of its right subtree,

• the height of this binary tree is 2 (and the height of the tree denoted by t0 is 0), and

• since

  • at depth 0, it has 1 node,
  • at depth 1, it has 2 nodes,
  • at depth 2, it has 4 leaves,

  the width of this binary tree is 4.

Properties of binary trees of natural numbers

Let us start with a structural property: Does a given binary tree of integers only contain non-negative numbers?

Intuitively, the unit-test procedure is simple to write – if the candidate procedure is applied to a tree containing anything but a non-negative integer as a leaf, it should return #f, and otherwise it should return #t:

(define positive-test-binary-tree-of-non-negative-integers?
  (lambda (candidate)
    (and (equal? (candidate 0) #t)
         (equal? (candidate 1) #t)
         (equal? (candidate (cons 0 1)) #t)
         (equal? (candidate (cons (cons 0 1) (cons 2 3))) #t)
         ;;; etc.
         )))

(define negative-test-binary-tree-of-non-negative-integers?
  (lambda (candidate)
    (and (equal? (candidate -1) #f)
         (equal? (candidate #t) #f)
         (equal? (candidate (cons 1 #t)) #f)
         (equal? (candidate (cons 1 -1)) #f)
         ;;; etc.
         )))

Formally, the predicate (i.e., Boolean-returning procedure) is specified inductively, following the structure of binary trees:

• leaf case (a.k.a. base case):

  • for any integer n (noting its syntactic representation as n),
    • if n is negative (i.e., n < 0), n does not denote [the leaf of] a binary tree that only contains non-negative integers; and
    • if n is non-negative (i.e., n >= 0), n denotes [the leaf of] a binary tree that only contains non-negative integers

• node case (a.k.a. induction step):

  for any values v1 and v2 (noting their syntactic representation as v1 and v2),

  • if both v1 and v2 are binary trees that only contain non-negative integers, then (cons v1 v2) denotes [the node of] a binary tree that only contains non-negative integers
  • otherwise, (cons v1 v2) does not denote [the node of] a binary tree that only contain non-negative integers

• remaining cases:

  for any Scheme value v (noting its syntactic representation as v) that is not an integer and not a pair, v does not denote [the leaf of] a binary tree that only contains non-negative integers

It looks like a small step – one that we shall take this coming week – to implement this predicate as a structurally recursive procedure mapping a Scheme value to a Boolean. However, since binary trees are constructed with cons, they might be cyclic, so caution is in order.

Towards computing the number of leaves of a given binary tree

The goal of this section is to prepare ourselves to implement a procedure number-of-leaves that counts the number of leaves in a Scheme value according to the BNF of binary trees within Scheme values. This procedure should pass the following unit test:

(define test-number-of-leaves
  (lambda (candidate)
    (and (equal? (candidate 32)
                 1)
         (equal? (candidate candidate)
                 1)
         (equal? (candidate (cons 32 33))
                 2)
         (equal? (candidate (cons 32 pair?))
                 2)
         (equal? (candidate (cons (cons 1 2) (cons 3 4)))
                 4)
         (equal? (candidate (cons 0 (cons (cons 1 2) (cons 3 4))))
                 5)
         (equal? (candidate (cons (cons 0 (cons (cons 1 2) (cons 3 4))) (cons 5 6)))
                 7)
         ;;; add more tests here
         )))

Let us define how to compute the number of leaves in a binary tree according to the following specification, which follows the inductive structure of binary trees:

• in English:

  • leaf case: given a Scheme value that is not a pair, the number of leaves in this Scheme value is 1.
  • node case: given two Scheme values v1 and v2 whose respective numbers of leaves are n1 and n2, the number of leaves in the pair whose car is v1 and whose cdr is v2 is the sum of n1 and n2.

• logically, the Scheme value v contains n leaves whenever the following judgment holds:

  (%number-of-leaves v n)
  

  This judgment is defined with the following proof rules:

  NUMBER-OF-LEAVES_LEAF	v is not a pair
  	(%number-of-leaves v 1)

  NUMBER-OF-LEAVES_NODE	(%number-of-leaves v1 n1)	(%number-of-leaves v2 n2)	where n = n1 + n2
  	(%number-of-leaves (cons v1 v2) n)

  Let us review these two rules:

  • The first rule, NUMBER-OF-LEAVES_LEAF, says that the number of leaves in v is 1 whenever v is not a pair.
  • The second rule, NUMBER-OF-LEAVES_NODE, says that if v1 contains n1 leaves and if v2 contains n2 leaves, then the pair whose car is v1 and whose cdr is v2 contains n1 + n2 leaves.

• functionally:

  • leaf case: for all Scheme values v that are not pairs, number-of-leaves (v) = 1
  • node case: for all Scheme values v that are pairs, number-of-leaves (v) = number-of-leaves (car (v)) + number-of-leaves (cdr (v))

Towards computing the number of nodes in a given binary tree

The goal of this section is to prepare ourselves to implement a procedure number-of-nodes that counts the number of nodes in a Scheme value according to the BNF of binary trees within Scheme values. This procedure should pass the following unit test:

(define test-number-of-nodes
  (lambda (candidate)
    (and (equal? (candidate 32)
                 0)
         (equal? (candidate candidate)
                 0)
         (equal? (candidate (cons 32 33))
                 1)
         (equal? (candidate (cons 32 pair?))
                 1)
         (equal? (candidate (cons (cons 1 2) (cons 3 4)))
                 3)
         (equal? (candidate (cons 0 (cons (cons 1 2) (cons 3 4))))
                 4)
         (equal? (candidate (cons (cons 0 (cons (cons 1 2) (cons 3 4))) (cons 5 6)))
                 6)
         ;;; add more tests here
         )))

Let us define how to compute the number of nodes in a binary tree according to the following specification, which follows the inductive structure of binary trees:

• in English:

  • leaf case: given a Scheme value that is not a pair, the number of nodes in this Scheme value is 0.
  • node case: given two Scheme values v1 and v2 whose respective numbers of nodes are n1 and n2, the number of nodes in the pair whose car is v1 and whose cdr is v2 is the sum of n1 and n2, plus 1.

• logically, the Scheme value v contains n nodes whenever the following judgment holds:

  (%number-of-nodes v n)
  

  This judgment is defined with the following proof rules:

  NUMBER-OF-NODES_LEAF	v is not a pair
  	(%number-of-nodes v 0)

  NUMBER-OF-NODES_NODE	(%number-of-nodes v1 n1)	(%number-of-nodes v2 n2)	where n = n1 + n2 + 1
  	(%number-of-nodes (cons v1 v2) n)

  Let us review these two rules:

  • The first rule, NUMBER-OF-NODES_LEAF, says that the number of nodes in v is 0 whenever v is not a pair.
  • The second rule, NUMBER-OF-NODES_NODE, says that if v1 contains n1 nodes and if v2 contains n2 nodes, then the pair whose car is v1 and whose cdr is v2 contains n1 + n2 + 1 leaves.

• functionally:

  • leaf case: for all Scheme values v that are not pairs, number-of-nodes (v) = 0
  • node case: for all Scheme values v that are pairs, number-of-nodes (v) = number-of-nodes (car (v)) + number-of-nodes (cdr (v)) + 1

Interlude

Alfrothul: Did you see that test-number-of-leaves and test-number-of-nodes use the same trees?

Anton: I didn’t particularly notice, but why not? This way, they are easier to compare. Also, gratuitous variations are rarely a good idea when writing programs.

Alfrothul: Did you compare the expected results, in each test?

Anton: Oh. They are comparable indeed.

Alfrothul: Do you think that this comparison holds true for any tree?

Anton: I guess that would be something to prove by structural induction...

Alfrothul: It doesn’t even look to hard.

Anton: So... The property we want to prove is that for any tree, its number of leaves is its number of nodes, plus 1.

Alfrothul: Dibs on the base case! A leaf contains one leaf and zero nodes.

Anton: Right – indeed for any integer n (noting its syntactic representation as n), evaluating (number-of-leaves n) yields 1, evaluating (number-of-nodes n) yields 0, and 1 = 0 + 1.

Alfrothul: Now for the induction case... We are given two trees t1 and t2 such as

• t1 contains l1 leaves and n1 nodes, and l1 = n1 + 1, and
• t2 contains l2 leaves and n2 nodes, and l2 = n2 + 1.

Anton: Let’s look at the tree consisting of a pair whose left subtree is t1 and whose right subtree is t2.

Alfrothul: This tree has l1 + l2 leaves.

Anton: And it has n1 + n2 + 1 nodes.

Alfrothul: Since l1 = n1 + 1...

Anton (helpfully interjecting a precision): Which is the first induction hypothesis.

Alfrothul (continuing): ...and l2 = n2 + 1,

Anton (interjecting another precision): Which is the second induction hypothesis.

Alfrothul: ... l1 + l2 = n1 + 1 + n2 + 1. And thanks.

Anton: So the number of leaves of this tree, i.e., l1 + l2, is indeed its number of nodes, i.e., n1 + n2 + 1, plus 1.

Alfrothul: So this comparison holds true for any tree.

Anton: Even when the tree is, like, imbalanced?

Alfrothul: That’s what the maths say. The grammar for binary trees is not just sound (all Scheme values, in particular when obtained using the constructor cons, represent binary trees if no pair has been mutated), it is also complete (all binary trees can be constructed using cons). So if it is a binary tree, no matter its shape, its number of leaves is its number of nodes, plus 1.

Bong-sun: Alfrothul, that was swift.

Alfrothul: Swift?

Bong-sun: The way you went from what the maths say to what the maths mean.

Alfrothul: Thanks – I guess.

The empty list

The empty list is written () and its associated predicate is null?:

> (list)
()
> (null? (list))
#t
> (null? 32)
#f
> (null? (cons 1 2))
#f
>

The empty list has a nickname: nil. If we want to use it in Scheme, presto, define it:

> (define nil (list))
> nil
()
> (define null nil)
> null
()
>

Lists

This section describes how lists are represented in Scheme, using pairs (as constructed using the cons predefined procedure) and the empty list (a predefined value):

• Proper lists consists of pairs that are linked from left to right through the cdr field of each pair, and that terminate with the empty list.

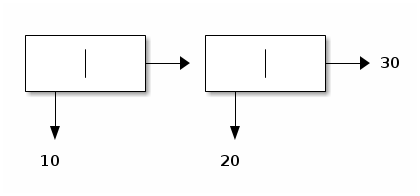
  For example, evaluating (cons 2 (cons 1 '())) yields the following proper list:

  

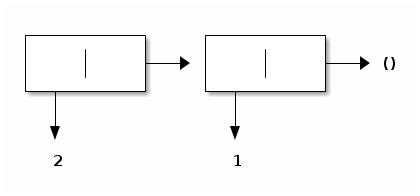
• Improper lists consists of pairs that are linked from left to right through the cdr field of each pair, and that terminate with something else than the empty list.

  For example, evaluating (cons 2 (cons 1 0)) yields the following improper list:

  

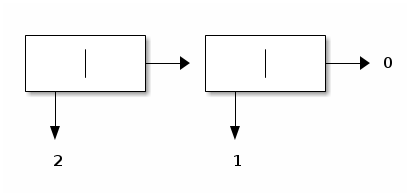
Proper lists

Pairs are used to construct singly linked proper lists as follows:

<proper-list-of-values> ::= ()
                          | (<value> . <proper-list-of-values>)

<value>                 ::= ...any Scheme value, including proper lists...

In other words, a proper list is constructed with nested calls to cons where the right-most call is given the empty list as a second argument. In other words again, proper lists are inductively specified as either the empty list (the nil case, a.k.a. the base case) or as the result of applying cons to a Scheme value and to a proper list (the cons case, a.k.a. the induction step).

Proper lists are constructed with pairs but by convention, and unlike pairs, they are printed without nested parentheses and without a dot at the end:

> (cons 1 '())
(1)
> (cons 2 (cons 1 '()))
(2 1)
> (cons 3 (cons 2 (cons 1 '())))
(3 2 1)
>

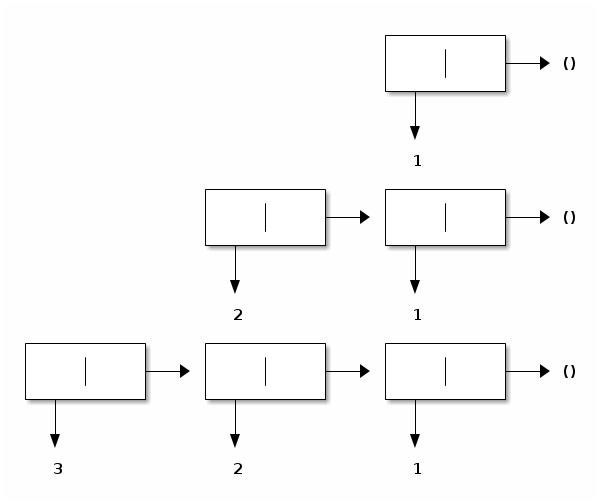
Graphically, proper lists are depicted as traditional linked lists with one forward link and no back link in each node:

To group a series of values in a list, rather than repeatedly calling cons, we use the variadic procedure list:

> (list 3 2 1)
(3 2 1)
>

Proper lists can be heterogeneous, in that their elements need not all have the same type:

> (list 1 "2" (list 3 4))
(1 "2" (3 4))
>

Graphically:

The predefined procedure string->list is unary and maps a string to the corresponding proper list of characters:

> (string->list "hello world")
(#\h #\e #\l #\l #\o #\space #\w #\o #\r #\l #\d)
> (string->list "")
()
>

It is an error to apply string->list to something else than a string. The left inverse of string->list is the unary predefined procedure list->string. It is an error to apply list->string to something else than a proper list of characters:

> (list->string (string->list "hello world"))
"hello world"
> (list->string (string->list ""))
""
>

Proper lists can be nested. For example, here is the list of the successive suffixes of the proper list (3 2 1):

> (list (list 3 2 1) (list 2 1) (list 1) (list))
((3 2 1) (2 1) (1) ())
>

Graphically:

Sublists can be shared. For example, here is the list of the shared successive suffixes of the proper list (3 2 1):

> (let* ([x0 '()]
         [x1 (cons 1 x0)]
         [x2 (cons 2 x1)]
         [x3 (cons 3 x2)])
    (list x3 x2 x1 x0))
((3 2 1) (2 1) (1) ())
>

Graphically:

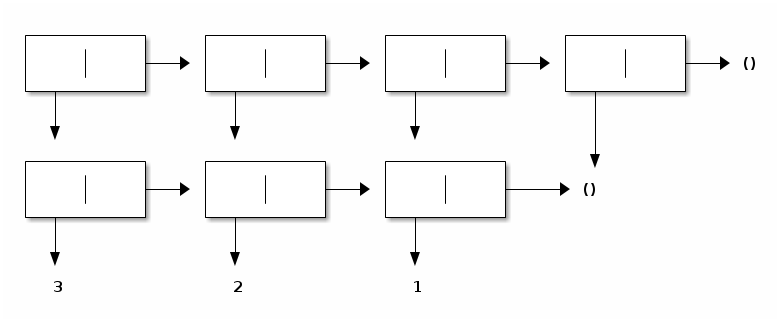
Proper lists can be arbitrarily nested, e.g., onion-style:

> (list 1
        (list 2
              (list 3
                    (list 4
                          '()
                          4)
                    3)
              2)
        1)
(1 (2 (3 (4 () 4) 3) 2) 1)
>

A proper list is terminated by the empty list, no matter what it contains, e.g., pairs:

> (list (cons 1 2) (cons 3 4) (cons 5 6))
((1 . 2) (3 . 4) (5 . 6))
> (list? (list (cons 1 2) (cons 3 4) (cons 5 6)))
#t
>

Graphically:

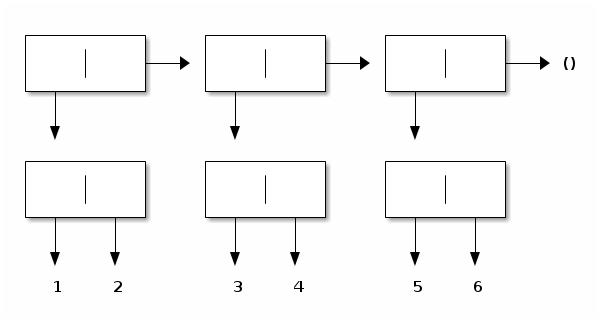
Naturally, proper lists lend themselves to much structurally recursive programming. Let us give two typical illustrations: one where we compute the length of a proper list, and one where we concatenate two proper lists.

Predefined procedure to test for a proper list

The predicate associated to proper lists is list?:

> (list? (cons (cons 1 2) '()))
#t
> (list? (cons 1 (cons 2 (cons 3 '()))))
#t
> (list? (cons 1 (cons 2 (cons 3 4))))
#f
>

Warning

Unlike the type predicate pair? that operates in constant time, the predicate list? operates in linear time: its argument needs to be traversed to check whether it terminates with the empty list or not (i.e., it terminates with another value than the empty list or it is cyclic).

Computing the length of a proper list

The length of a proper list can be computed with the predefined procedure length:

> (list)
()
> (length (list))
0
> (list 1)
(1)
> (length (list 1))
1
> (list 3 2 1)
(3 2 1)
> (length (list 3 2 1))
3
>

Here is a unit-test procedure that accounts for this scenario:

(define unit-tests-for-length_proper-list
  (lambda (candidate)
    (and (equal? (candidate (list))
                 0)
         (equal? (candidate (list 1))
                 1)
         (equal? (candidate (list 3 2 1))
                 3)
         ;;; add more tests here
         )))

Chez Scheme’s predefined procedure length passes this unit test:

> (unit-tests-for-length_proper-list length)
#t
>

Let us define how to compute the length of a proper list according to the following recipe, which follows the inductive structure of proper lists:

• in English:

  • nil case: the length of the empty list is 0.
  • cons case: the length of a non-empty proper list is the successor of the length of the cdr of that proper list.

• logically, a list vs has length n whenever the following judgment holds:

  (%length vs n)
  

  This judgment is defined with the following proof rules, noting the empty list with nil:

  LENGTH_NIL
  	(%length nil 0)

  LENGTH_CONS	(%length vs m)	where n = m + 1
  	(%length (cons v vs) n)

  Let us review these two rules:

  • The first rule, LENGTH_NIL, is an axiom: it says that the length of the empty list is 0.
  • The second rule, LENGTH_CONS, says that if the length of vs is m, then the length of consing a value v onto vs is the successor of m.

• functionally, noting the empty list with nil:

  • nil case: length (nil) = 0
  • cons case: for all values v and proper lists vs, length (cons (v, vs)) = 1 + (length vs)

Concatenating a proper list to another proper list

Here is a scenario that illustrates the essential properties of concatenating proper lists in Scheme, using the predefined procedure append:

> (list)
()
> (append (list) (list))
()
> (list 4 5 6)
(4 5 6)
> (append (list) (list 4 5 6))
(4 5 6)
> (append (list 4) (list 5 6))
(4 5 6)
> (append (list 4 5) (list 6))
(4 5 6)
> (append (list 4 5 6) (list))
(4 5 6)
>

In words:

• concatenating the empty list to any other proper list yields this other proper list,
• concatenating any proper list to the empty list yields this proper list, and
• concatenating a proper list containing v1, v2, etc. to another proper list containing w1, w2, etc. yields a proper list that contains v1, v2, etc. followed by w1, w2, etc.

Here is a unit test that captures these essential properties:

(define unit-tests-for-append_proper-list
  (lambda (candidate)
    (and (equal? (candidate (list) (list))
                 (list))
         (equal? (candidate (list) (list 4 5 6))
                 (list 4 5 6))
         (equal? (candidate (list 4) (list 5 6))
                 (list 4 5 6))
         (equal? (candidate (list 4 5) (list 6))
                 (list 4 5 6))
         (equal? (candidate (list 4 5 6) (list))
                 (list 4 5 6))
         ;;; add more tests here
         )))

Chez Scheme’s predefined procedure append passes this unit test:

> (unit-tests-for-proper-list-append append)
#t
>

Here is a second scenario to visualize the concatenation of two proper lists, where the two input lists and the output list are given a name:

> (define xs (list 1 2 3))
> xs
(1 2 3)
> (define ys (list 4 5 6))
> ys
(4 5 6)
> (define xs-xs (append xs xs))
> (define xs-ys (append xs ys))
> (define ys-xs (append ys xs))
> (define ys-ys (append ys ys))
> xs-xs
(1 2 3 1 2 3)
> xs-ys
(1 2 3 4 5 6)
> ys-xs
(4 5 6 1 2 3)
> ys-ys
(4 5 6 4 5 6)
> (append xs-xs ys-ys)
(1 2 3 1 2 3 4 5 6 4 5 6)
>

Let us define the concatenation of two proper lists according to the following recipe, which follows the inductive structure of proper lists:

• in English:

  • nil case: concatenating the empty list to a proper list gives that proper list.
  • cons case: given a non-empty proper list whose car is a value v and whose cdr is the proper list vs, and given a second proper list, concatenating this non-empty list to this second list yields a proper list whose car is v and whose cdr is the result of concatenating vs to this second proper list.

• logically, a list zs is the concatenation of the lists xs and ys whenever the following judgment holds:

  (%append xs ys zs)
  

  This judgment is defined with the following proof rules, noting the empty list with nil:

  APPEND_NIL
  	(%append nil ys ys)

  APPEND_CONS	(%append xs ys zs)
  	(%append (cons x xs) ys (cons x zs))

  Let us review these two rules:

  • The first rule, APPEND_NIL, is an axiom: it says that ys is the concatenation of the empty list and ys.
  • The second rule, APPEND_CONS, says that if zs is the concatenation of xs and ys, then for any x, (cons x zs) is the concatenation of (cons x xs) and ys.

• functionally, noting the empty list with nil:

  • nil case: for all proper lists ws, append_proper-list (nil, ws) = ws
  • cons case: for all values v and for all proper lists vs and ws, append_proper-list (cons (v, vs), ws) = v :: append_proper-list (vs, ws)

Three (in the sense of two) questions:

1. Is there any sharing between the two lists that are passed to append_proper-list and the list it returns?
2. If the answer to the first question is “yes”, how would one modify the definition of append_proper-list so that there is no sharing at all?
3. If the answer to the first question is “no”, how would one modify the definition of append_proper-list so that there is some sharing?

(Hint for the first question: what does append_proper-list return when its first argument is the empty list?)

Food for thought about the predefined list-concatenation procedure in Chez Scheme, append:

• If you had to decide what should be the result of giving more than two arguments to append, what would be this result? Why? How does your decision compare with the behavior of Chez Scheme?
• If you had to decide what should be the result of giving one argument to append, what would be this result? Why? How does your decision compare with the behavior of Chez Scheme?
• If you had to decide what should be the result of giving no argument to append, what would be this result? Why? How does your decision compare with the behavior of Chez Scheme?

Improper lists

An improper list is constructed with cons in a way that does not terminate with the empty list:

> (list? (cons 1 (cons 2 (cons 3 4))))
#f
>

Graphically:

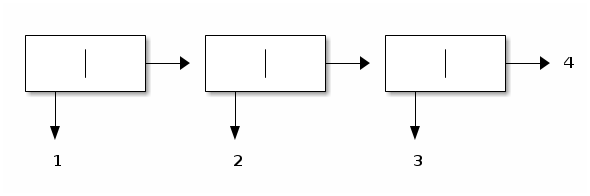
The trailing value is printed after a dot:

> (cons 1 (cons 2 (cons 3 4)))
(1 2 3 . 4)
>

A pair whose cdr is not the empty list is called a dotted pair.

Like proper lists, improper lists can be heterogeneous, nested, and shared.

Cyclic lists

The cdr of one of the pairs of a cyclic list is one of the pairs in this list.

Examples:

Cyclic lists are detected using the resident list? predicate:

> (define p (cons 0 '()))
> (set-cdr! p p)
> (list? p)
#f
> (list? (cons 1 p))
#f
> (list? (cons 2 (cons 1 p)))
#f
>

Resources

• The Scheme code for the present lecture note (latest version: 07 Sep 2025).

Version

Expanded the section about cyclic lists [13 Sep 2025]

Created [07 Sep 2025]