The Scheme programming language, continued

See also

The Scheme Programming Language

by R. Kent Dybvig

Goal

This chapter continues introducing the Scheme programming language from scratch.

Resources

• The Scheme code for the present lecture note (latest version: 07 Sep 2025).

Core special form: quote

<quote-expression>   ::= (quote <quotation>)

<quotation>          ::= <number>
                       | <boolean>
                       | <character>
                       | <string>
                       | <symbol>
                       | ()
                       | <quotation-compound>

<symbol>             ::= <identifier>

<quotation-compound> ::= (<quotation> . <quotation>)

Note: (quote <quotation>) is abbreviated '<quotation>.

A quote-expression is used to introduce a pre-evaluated value.

Numbers, Booleans, characters and strings are self-evaluating in Scheme, and so they can indifferently be quoted or not:

> (quote 2)
2
> '2
2
> '#t
#t
>

Of special interest is the representation of (Scheme) programs as data objects. To this end, a Scheme symbol is a special kind of value to represent variables and keywords when representing programs as data:

> 'x
x
> 'lambda
lambda
> (symbol? 'x)
#t
> (symbol? "x")
#f
> (symbol=? 'foo 'foo)
#t
> (symbol=? 'foo 'bar)
#f
>

The empty list can also be quoted:

> '()
()
> (quote ())
()
> (equal? '() (list))
#t
>

Compound values can also be quoted, as elaborated later in this lecture note for lists:

> (list 'lambda (list 'x) 'x)
(lambda (x) x)
> '(lambda (x) x)
(lambda (x) x)
>

Quotation is a convenient notation to represent values syntactically, as if they were the result of an evaluation. (Look how (lambda (x) x) was obtained just above: the first time by explicit list construction, and the second time by quotation.)

By default, Chez Scheme pretty-prints its output as if it were a Scheme expression:

> '(define PI (lambda (mt f) ((lambda (x) (x x)) (lambda (x) (lambda (g) (if (<= g 0) mt (f ((x x) (1- g)))))))))
(define PI
  (lambda (mt f)
    ((lambda (x) (x x))
      (lambda (x)
        (lambda (g) (if (<= g 0) mt (f ((x x) (1- g)))))))))
>

Han Solo (teasingly): You like me because I’m a scoundrel.

Princess Leia (outraged): What?!?

Han Solo (surprised): What, “What?”?

Luke Skywalker (entering the room): What, “What, “What?”?”?

—Star Wars apocryphal

Nested quotations provide a concise way to represent

• representations,
• representations of representations,
• representations of representations of representations, etc.,

Since quotation lets us represent values syntactically, in a way that is represented prior to evaluation, evaluating a quoted value has the effect of “removing the quote”. This removal is particularly visible for nested quotations:

> '''x
''x
> ''x
'x
> 'x
x
> x

Exception: variable x is not bound
Type (debug) to enter the debugger.
>

Foresight is a source of déjà vu.

To close, let us revisit the abbreviation of (quote <quotation>) as '<quotation>. The two are indistinguishable, which is good to know when programming, e.g., a syntax checker for Scheme:

> (equal? 'whatever (quote whatever))
#t
> (equal? ''whatever (quote (quote whatever)))
#t
> (equal? ''whatever '(quote whatever))
#t
> (equal? ''whatever (quote 'whatever))
#t
> (equal? '(quote whatever) (quote 'whatever))
#t
>

Derived special forms: let

<let-expression> ::= (let <let-header>
                       <let-body>)

<let-body>       ::= <expression>

<let-header>     ::= ({<let-binding>}*)

<let-binding>    ::= [<variable> <let-definiens>]

<let-definiens>  ::= <expression>

Note: in most other dialects of Scheme, let-bindings are not delimited with square brackets by default but with ordinary parentheses.

A let-expression consists of a header and a body:

• The body is an expression.
• The header consists of a number of clauses – the let-bindings – possibly zero.
• In the header of a let-expression, each clause consists of a variable and a definiens, which is an expression.
• All the variables declared in the header of a let-expression must be distinct.

When evaluating the expression

(let ([x1 e1] [x2 e2] ... [xN eN]) e0)

in an environment, the sub-expressions e1, e2, ..., and eN are evaluated in an unspecified order:

• If evaluating one of these sub-expressions does not terminate, then evaluating this let-expression does not terminate either.

• If evaluating one of these sub-expressions raises an error, then evaluating this let-expression raises this error too.

• Otherwise evaluating all of these sub-expressions yields the values v1, v2, ..., and vN.

  Evaluating this let-expression then reduces to evaluating e0 in an environment that extends the environment of the let-expression by binding each name x1, x2, ..., and xN to v1, v2, ..., and vN.

For example, the following expressions are evaluated in the initial environment environment where list denotes the variadic procedure that packages its arguments into a list and that we have used above.

• (let () (list)) evaluates to ().

  The header is empty. The body is (list). It is evaluated in the same environment as that of the let-expression, i.e., the initial environment. There are no actual parameters in the application of list, and so the body evaluates to the empty list.

• (let ([a 1]) (list a)) evaluates to (1).

  The header contains one let-binding. The variable is a, the definiens is 1, and the body is (list a). It is evaluated in an extension of the initial environment where a denotes 1. There is one actual parameter in the application of list – a – which evaluates to 1, and so the body evaluates to the list containing 1.

• (let ([a 1] [b 2]) (list a b)) evaluates to (1 2).

  The header contains two let-bindings. The variables are a and b, the definienses are 1 and 2, and the body is (list a b). It is evaluated in an extension of the initial environment where a denotes 1 and b denotes 2. There are two actual parameters in the application of list – a and b – which evaluate to 1 and 2, respectively, and so the body evaluates to the list containing 1 and 2.

• (let ([a 1] [b 2] [c 3] [d 4]) (list a b c d)) evaluates to (1 2 3 4).

  The header contains four let-bindings. The variables are a, b, c, and d, the definienses are 1, 2, 3, and 4, and the body is (list a b c d). It is evaluated in an extension of the initial environment where a denotes 1, b denotes 2, c denotes 3, and d denotes 4. There are four actual parameters in the application of list – a, b, c, and d – which evaluate to 1, 2, 3, and 4, respectively, and so the body evaluates to the list containing 1, 2, 3, and 4.

Landin’s correspondence principle

The let-expression (let ([x1 e1] [x2 e2] ... [xN eN]) e0) and the application ((lambda (x1 x2 ... xN) e0) e1 e2 ... eN) are observationally equivalent.

Peter Landin: Thank you.

Mimer: Prof. Landin! Thanks so much for jumping by!

Interlude

Bong-sun: Aha.

Dana: Aha?

Bong-sun: Landin’s correspondence principle explains the similarity between the description of how applications are evaluated and the description of how let-expressions are evaluated.

Mimer: Good point, Bong-sun.

Dana: Question.

Mimer: Yes, Dana?

Dana: Suppose we evaluate (let ([x1 e1] [x2 e2]) e0).

Halcyon: Or ((lambda (x1 x2) e0) e1 e2).

Mimer: Yes?

Dana: The description says that e1 and e2 are evaluated in either order.

Mimer: Yes.

Dana: What if evaluating one does not terminate and evaluating the other raises an error? What is the overall result of evaluating the let-expression?

Halcyon: Or the application.

Mimer: The result is either divergence or an error.

Dana: So the semantics is ambiguous?

Mimer: No, it is deliberately unspecified so that programmers do not rely on the implicit order of evaluation. Their program should say whether e1 or e2 is evaluated first. And then there is no ambiguity.

Bong-sun: You mean we should write either of the following expressions?

(let ([v1 e1])
  (let ([x1 v1] [x2 e2])
    e0))

(let ([v2 e2])
  (let ([x1 e1] [x2 v2])
    e0))

Anton: Or perhaps rather:

(let ([x1 e1])
  (let ([x2 e2])
    e0))

(let ([x2 e2])
  (let ([x1 e1])
    e0))

Pablito: Either way, the outer let-expression makes it clear which of e1 or e2 is evaluated first.

Mimer: Yes, though for the first expression, do make sure that v1 does not occur in e2, for the second expression, do make sure that v2 does not occur in e1, for the third expression, do make sure that x1 does not occur in e2, and for the fourth expression, do make sure that x2 does not occur in e1, so that the name in your outer let-expression does not shadow an ocurrence of this name in the definiens of your inner let-expression.

Anton: Huh, can you provide an example?

Mimer: Of course. Consider

(lambda (x)
  (let ([x (foo x)] [y (bar x)])
    ...))

Alfrothul: Right. It would be incorrect to write

(lambda (x)
  (let ([x (foo x)])
    (let ([y (bar x)])
      ...)))

Bong-sun: Right. In the inner let-expression, the occurrence of x in the application of bar should refer to the formal parameter of the lambda, not to the name declared in the outer let-expression.

Anton: OK. So we should use a new name:

(lambda (x)
  (let ([z (foo x)])
    (let ([x z] [y (bar x)])
    ...))

Mimer: Yup.

Let-expressions, continued

Let-expressions can be nested. This nesting is regulated by lexical scope: the most recently declared variable is the one whose binding is in effect. The following expressions are evaluated in an environment where list is globally bound to a variadic procedure that packages its arguments into a list.

• For example, the expression

  (let ([a 1])
    (let ([b 2])
      (list a b)))
  

  evaluates to (1 2). Graphically:

  

  The expression (list a b) is evaluated in an environment where b denotes 2, a denotes 1, and list is globally bound.

• When two nested let-expressions declare the same variable, the inner binding “shadows” the outer binding in the extended environment. So for example, the expression

  (let ([a 1])
    (let ([a 2])
      (list a)))
  

  evaluates to (2). Graphically:

  

  The expression (list a) is evaluated in an environment where a denotes 2 and list is globally bound. The inner binding of a (to 2) shadows its outer binding (to 1).

• For another example of shadowing, the expression

  (let ([a 1] [b 2] [c 3])
    (let ([c b])
      (list a b c)))
  

  evaluates to (1 2 2) because the inner declaration of c binds it to the denotation of b, which is 2. The inner binding of c (to 2) “shadows” its outer binding (to 3). Graphically:

  

  The expression (list a b c) is evaluated in an environment where c denotes 2, b denotes 2, a denotes 1, and list is globally bound. (The outer binding of c to 3 is shadowed.)

• In the previous example, even if b is re-declared in the scope of c, the denotation of c is unaffected, and so an expression such as

  (let ([a 1] [b 2] [c 3])
    (let ([c b])
      (let ([b 22])
        (list a b c))))
  

  evaluates to (1 22 2). Graphically:

  

  The expression (list a b c) is evaluated in an environment where b denotes 22, c denotes 2, a denotes 1, and list is globally bound. (The outer bindings of c to 3 and of b to 2 are shadowed.)

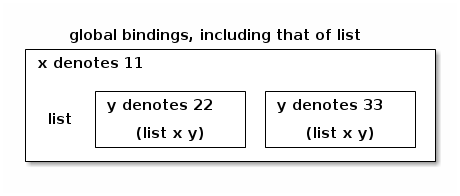
• Environment extensions co-exist without interference, and an expression such as

  (let ([x 11])
    (list (let ([y 22])
            (list x y))
          (let ([y 33])
            (list x y))))
  

  evaluates to ((11 22) (11 33)). Graphically:

  
  • The first occurrence of (list x y) is evaluated in an environment where y denotes 22, x denotes 11, and list is globally bound.
  • The second occurrence of (list x y) is evaluated in an environment where y denotes 33, x denotes 11, and list is globally bound.

  Note: the order in the boxes does not matter, what matters is their nesting. For example, the boxes above can be drawn just as well as follows:

  

  Likewise, the Scheme expression could also have been written horizontally:

  (let ([x 11])
    (list (let ([y 22]) (list x y)) (let ([y 33]) (list x y))))
  

  One should write and draw whatever is simplest and most readable.

• Finally, shadowed bindings in lexical scope and non-interfering co-existence of environment extensions combine harmoniously. So for example, an expression such as

  (let ([x 11])
    (list (let ([y 22])
            (let ([x 44])
              (list x y)))
          (list x x)
          (let ([y 33])
            (let ([y 55])
              (list x y)))))
  

  evaluates to ((44 22) (11 11) (11 55)). Graphically:

  
  • The first occurrence of (list x y) is evaluated in an environment where x denotes 44, y denotes 22, and list is globally bound. (The outer binding of x to 11 is shadowed.)
  • The expression (list x x) is evaluated in an environment where x denotes 11 and list is globally bound.
  • The second occurrence of (list x y) is evaluated in an environment where y denotes 55, x denotes 11, and list is globally bound. (The outer binding of y to 33 is shadowed.)

Lexical scope and local procedures

All in all, a variable can be

• pre-declared (e.g., list) and bound in the initial environment,
• declared with define and bound in the global environment,
• declared as the formal parameter of a lambda-abstraction and locally bound in the current environment, or
• declared as a variable in a let-expression and locally bound in the current environment.

Scheme is lexically scoped in that the most recently declared variable in the text of a program is the one whose binding is in effect, which was depicted above with nested boxes. This nesting applies for declaring local procedures. So for example, an expression such as

(let ([x 10])
  (let ([foo (lambda ()
               x)])
    (let ([x 20])
      (list x (foo)))))

evaluates to (20 10). Graphically:

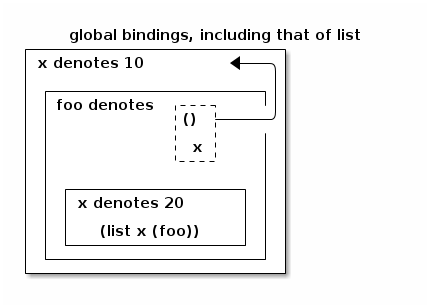
• foo denotes a parameterless procedure (represented with a dashed box just above) whose lexical scope (represented with an arrow going out of the dashed box just above) contains the binding of x to 10.
• (list x (foo)) is evaluated in an environment where x denotes 20, foo denotes a parameterless procedure, and list is globally bound.

About the dashed box:

• the top part contains the formal parameters of the lambda-abstraction, and
• the bottom part contains its body.

Here is another example. The expression

(let ([x 10] [y 20] [z 30])
  (let ([foo (lambda (y t)
               (list x y t))])
    (let ([x 20])
      (list x (foo 40 z)))))

evaluates to (20 (10 40 30)). Graphically:

• foo denotes a dyadic procedure (the dashed box just above) whose lexical scope (the arrow just above) contains the binding of x to 10 and the global binding of list.
• (list x (foo 40 z)) is evaluated in an environment where x denotes 20, foo denotes a dyadic procedure, z denotes 30, and list is globally bound.

Note: the term “lexical scope” is used interchangeably with the term “static scope”. In an implementation, the environment is represented as a last-in, first-out “static chain”, and the procedure calls are represented as a last-in, first-out “dynamic chain”. In a statically scoped language such as Scheme, variables are looked up along the static chain, and in a dynamically scoped language such as Lisp, variables are looked up along the dynamic chain. So if Scheme was dynamically scoped, the expression

(let ([x 10])
  (let ([foo (lambda ()
               x)])
    (let ([x 20])
      (list x (foo)))))

would evaluate to (20 20) because the latest dynamic binding of x in the denotation of foo is 20.

A concrete example of dynamic scope in Emacs Lisp

Emacs is implemented in Emacs Lisp, which is dynamically scoped, so it provides a convenient setting to illustrate dynamic scope.

1. Let us globally declare a variable, x, to denote 10:

   (setq x 10)
   

   Henceforth, evaluating x yields 10.

   (Concretely, one can edit the *scratch* buffer, which is a promptless read-eval-print loop. To signal that the expression we have typed is to be read and then evaluated, one should type C-j.)

2. Let us globally declare another variable, foo, to denote an 0-ary anonymous function whose body is x:

   (fset 'foo (lambda () x))
   

   Henceforth, evaluating (foo) yields 10.

3. Let us locally declare x to denote 20 and in that local scope, let us evaluate (foo):

   (let ((x 20))
     (foo))
   

   The result is 20 because the local variable x dynamically shadows the global variable x.

4. Afterwards, we can verify that evaluating (foo) yields 10.

In contrast, Scheme is lexically scoped, and so the result of evaluating (foo) in an environment where x is locally bound to 20 yields 10:

> (define x 10)
> (define foo (lambda () x))
> (foo)
10
> (let ([x 20]) (foo))
10
> (foo)
10
>

Evaluating (foo) always yields the global denotation of x because evaluating (lambda () x) in a lexical environment yields a procedure whose body is evaluated in (an extension of) this lexical environment, irrespective of the environment in which this procedure was applied.

Core special forms: define, revisited

Global bindings live at the top of the lexical-scope chain, as illustrated in the following scenario:

> (define x0 1)
> (let ([x1 10])
    (let ([x2 100] [x3 1000])
      (let ([x4 10000] [x5 100000] [x6 1000000])
        (list x0 x1 x2 x3 x4 x5 x6))))
(1 10 100 1000 10000 100000 1000000)
> (let ([x1 10])
    (let ([x2 100] [x3 1000])
      (let ([x4 10000] [x5 100000] [x6 1000000])
        (let ([list +])
          (list x0 x1 x2 x3 x4 x5 x6)))))
1111111
>

In the second interaction, list denotes the denotation of +, i.e., the addition procedure. Graphically:

Derived special forms: let*

<letstar-expression> ::= (let* <letstar-header>
                           <letstar-body>)

<letstar-body>       ::= <expression>

<letstar-header>     ::= ({<letstar-binding>}*)

<letstar-binding>    ::= [<variable> <letstar-definiens>]

<letstar-definiens>  ::= <expression>

Note: in most other dialects of Scheme, let*-bindings are not delimited with square brackets by default but with ordinary parentheses.

Except for the star in its name, a let*-expression looks like a let-expression. It has a header (a number of clauses – the let*-bindings – possibly zero) and a body (an expression). A let*-expression such as

(let* ([x1 e1]
       [x2 e2]
       ...
       [xN eN])
  e0)

abbreviates the following let-expression:

(let ([x1 e1])
  (let ([x2 e2])
    ...
      (let ([xN eN])
        e0)...))

So for example,

(let* ([a 1] [b 2])
  (list a b))

abbreviates

(let ([a 1])
  (let ([b 2])
    (list a b)))

and evaluates to (1 2).

Also, a let*-definiens can refer to an earlier variable in the let*-header. So for example,

(let* ([x 10] [y 20] [x y])
  (list x y))

evaluates to (20 20). Graphically:

• The definiens y is evaluated in an environment where y denotes 20 and x denotes 10.
• The expression (list x y) is evaluated in an environment where x denotes 20, y denotes 20, and list is globally bound. (The outer binding of x to 10 is shadowed.)

Whereas a let-expression declares local variables and binds them in parallel, a let*-expression declares local variables and binds them sequentially:

> (let* ([x (time 10)] [y (time 20)] [z (time 30)])
    (list x y z))
(time 10)
    no collections
    0 ms elapsed cpu time
    0 ms elapsed real time
    0 bytes allocated
(time 20)
    no collections
    0 ms elapsed cpu time
    0 ms elapsed real time
    0 bytes allocated
(time 30)
    no collections
    0 ms elapsed cpu time
    1 ms elapsed real time
    0 bytes allocated
(10 20 30)
>

Resources

• The Scheme code for the present lecture note (latest version: 07 Sep 2025).

Version

Added the interlude about Landin’s correspondence principle and the concrete example of dynamic scope in Emacs Lisp [13 Sep 2025]

Created [07 Sep 2025]