Mini-project about depth-first and breadth-first traversals

The goal of this mini-project is to spell out depth-first and breadth-first traversals by solving Exercise 7 from Week 12 in detail.

In the accompanying resource file, a type of binary tree is defined with a payload in the leaves:

type 'a binary_tree =
  | Leaf of 'a
  | Node of 'a binary_tree * 'a binary_tree;;

Four tree-traversing functions are defined that collect the payloads of any given tree into a list:

• traverse_foo_lifo : 'a binary_tree -> 'a list,
• traverse_foo_fifo : 'a binary_tree -> 'a list,
• traverse_bar_lifo : 'a binary_tree -> 'a list, and
• traverse_bar_fifo : 'a binary_tree -> 'a list.

Friendly hints about the extensional questions:

• “extensional” means that the question are about the “what” of the traversal;
• draw the four binary trees based on the convention that in Node (x, y), x denotes the left subtree and y denotes the right subtree.

For example, the tree Node (Node (Leaf 3, Leaf 9), Leaf 5) is depicted as follows:

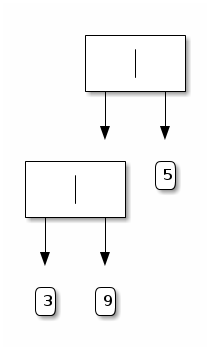
Friendly hints about the intensional questions:

• “intensional” means that the question are about the “how” of the traversal;
• use the traced versions of traverse_foo_lifo, traverse_foo_fifo, traverse_bar_lifo, and traverse_bar_fifo provided in the resource file to visualize how the traversals are achieved.

Extensional question #1

Analyze the output of these tree-traversing functions on the four given trees t1, t2, t3, and t4. (In each case, one of the resulting lists stands out.)

Extensional question #2

Characterize the traversal that each of these functions implements, using the (self-explanatory) terms “depth first”, “breadth first”, “left to right”, and “right to left”.

Extensional question #3

Test your characterization with 4 new telling examples (and explain why you find them telling).

Subsidiary question #1 (optional)

Neither traverse_foo nor traverse_bar are structurally recursive (and so could not be written using fold_binary_tree). Why is that?

Subsidiary question #2 (optional)

1. Could you write a version of traverse_foo_lifo that is structurally recursive (and so could be written using fold_binary_tree)? If so, do it. Otherwise, say why.
2. Could you write a version of traverse_foo_fifo that is structurally recursive (and so could be written using fold_binary_tree)? If so, do it. Otherwise, say why.
3. Could you write a version of traverse_bar_lifo that is structurally recursive (and so could be written using fold_binary_tree)? If so, do it. Otherwise, say why.
4. Could you write a version of traverse_bar_fifo that is structurally recursive (and so could be written using fold_binary_tree)? If so, do it. Otherwise, say why.

Closing question (for the over-achievers)

Implement a functor (see Section Functors in the lecture notes of Week 12) that is parameterized by a queue in a way such that

• instantiating this functor with Lifo yields a module containing two functions, one equivalent to traverse_foo_lifo and the other to traverse_bar_lifo, and
• instantiating this functor with Fifo yields a module containing two functions, one equivalent to traverse_foo_fifo and the other to traverse_bar_fifo.

Resources

• The OCaml code for the present mini-project (latest version: 07 Apr 2020).

Version

Fixed the URL of the first reference to the resource file, thanks to Guo Ziting’s eagle eye [09 May 2020]

Added error messages in the unit-test functions [07 Apr 2020]

Spelled out the questions and added the resource file [06 Apr 2020]

Added the announcement about the stand-alone restatement [05 Apr 2020]

Created [04 Apr 2020]