Polymorphic lists in OCaml, continued¶
The goal of this lecture note is to continue our exploration of polymorphic lists in OCaml.
Resources¶
- The OCaml code for the present lecture note (latest version: 14 Mar 2020).
Example: copying a list¶
Let us implement a function that, given a list, returns a copy of this list:
let test_list_copy_int candidate =
(* intuitive tests: *)
let b0 = (candidate [] = [])
and b1 = (candidate [0] = [0])
and b2 = (candidate [1; 0] = [1; 0])
(* structural tests: the inductive step (the base case is already above) *)
and b3 = (let n = Random.int 100
and ns' = atoi (Random.int 100)
in candidate (n :: ns') = n :: candidate ns')
(* properties: copying a list yields a list with the same length *)
and b4 = (let n = Random.int 100
in let ns = atoi n
in List.length (candidate ns) = n)
in b0 && b1 && b2 && b3 && b4;;
We can test this unit-test function with the identity function:
# test_list_copy_int (fun ns -> ns);;
- : bool = true
#
The copy function is defined following the inductive structure of lists:
base case:
concatenating the empty list yields the empty list
induction step:
for any list ys' whose copy yields a list zs (which is the induction hypothesis), copying x :: ys' yields x :: zs
Since the unit-test function tests both the base case and the induction step, it provides code coverage if the implementation is structurally recursive, which is it is about to be. Here is the skeleton of the copy function:
let list_copy_v0 xs_given =
let rec visit xs =
match xs with
| [] ->
...
| x :: xs' ->
let zs = visit xs'
in ...
in visit xs_given;;
Let us fill the blanks:
in the base case, the result is [], and
in the induction step, the result is obtained by cons’ing x to the result of the recursive call:
let list_copy_v0 xs_given = let rec visit xs = match xs with | [] -> [] | x :: xs' -> let zs = visit xs' in x :: zs in visit xs_given;;
This implementation is structurally recursive (since it follows the inductive structure of its input) and it passes the unit test:
# test_list_copy_int list_copy_v0;;
- : bool = true
#
In the induction step, the let-expression that declares zs', in the definition of visit, is cosmetic and so we can unfold it:
let list_copy_v1 xs_given =
let rec visit xs =
match xs with
| [] ->
[]
| x :: xs' ->
x :: visit xs'
in visit xs_given;;
(The expressions let zs = visit xs' in x :: zs and x :: zs are observationally equivalent since in both cases, visit xs' is evaluated first since the arguments of :: are evaluated from right to left.)
This simplified implementation is still structurally recursive and it passes the unit test:
# test_list_copy_int list_copy_v1;;
- : bool = true
#
Food for thought:
- the result of list_copy_v0 and list_copy_v1 is structurally equal (=) to the given list to copy;
- the result of the identity function, which also passes the unit tests, is physically equal (==) to the given list to copy.
Example: concatenating two lists¶
Let us implement a function that, given two lists, prepends the first to the second and yields the resulting list:
let test_list_append_int candidate =
(* two handpicked lists: *)
let b0 = (candidate [1; 2; 3] [4; 5] = [1; 2; 3; 4; 5])
(* etc. *)
in b0;;
The two input lists (calling them ns1 and ns2) are depicted as follows:
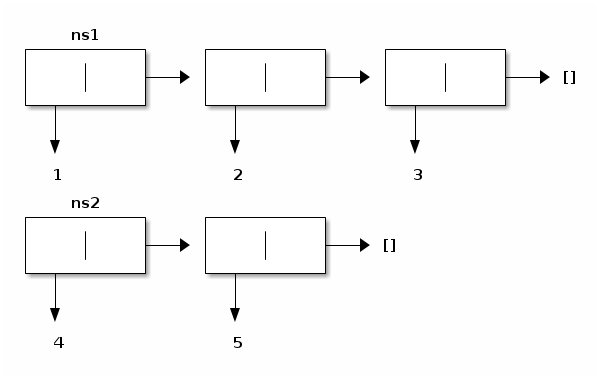
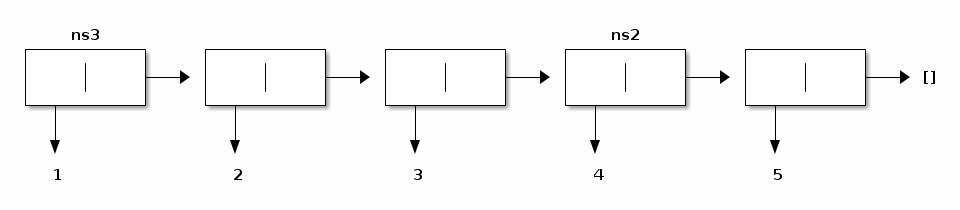
The output list (calling it ns3) is depicted as follows:
OCaml provides a predefined append function:
# test_list_append List.append;;
- : bool = true
#
It also offers syntactic sugar for this predefined append function, the infix operator @:
# test_list_append (fun xs ys -> xs @ ys);;
- : bool = true
# test_list_append (@);;
- : bool = true
#
Also, the second list is shared in the output list:
# let ns1 = [1; 2; 3];;
val ns1 : int list = [1; 2; 3]
# let ns2 = [4; 5];;
val ns2 : int list = [4; 5]
# List.tl (List.tl (List.tl (ns1 @ ns2))) == ns2;;
- : bool = true
#
The append function is defined following the inductive structure of lists:
base case:
concatenating the empty list to any other list yields this other list
induction step:
for any lists xs' and ys whose concatenation yields a list zs (which is the induction hypothesis), concatenating x :: xs' and ys yields x :: zs
And now we can beef up the unit-test function:
let test_list_append_int candidate =
(* two handpicked lists: *)
let b0 = (candidate [1; 2; 3] [4; 5] = [1; 2; 3; 4; 5])
(* an instance of the base case: *)
and b1 = (candidate [] [1; 0] = [1; 0])
(* successive instances of the induction step: *)
and b2 = (candidate [2] [1; 0] = [2; 1; 0])
and b3 = (candidate [3; 2] [1; 0] = [3; 2; 1; 0])
and b4 = (candidate [4; 3; 2] [1; 0] = [4; 3; 2; 1; 0])
(* other handpicked lists: *)
and b5 = (candidate [10; 20] [] = [10; 20])
(* etc. *)
in b0 && b1 && b2 && b3 && b4 && b5;;
Since the unit-test function tests both the base case and the induction step, it provides code coverage if the implementation is structurally recursive, which is it is about to be. Here is the skeleton of the concatenation function:
let list_append_v0 xs_given ys_given =
let rec visit xs =
match xs with
| [] ->
...
| x :: xs' ->
let zs = visit xs'
in ...
in visit xs_given;;
Let us fill the blanks:
in the base case, the result is ys_given, and
in the induction step, the result is obtained by cons’ing x to the result of the recursive call:
let list_append_v0 xs_given ys_given = let rec visit xs = match xs with | [] -> ys_given | x :: xs' -> let zs = visit xs' in x :: zs in visit xs_given;;
This implementation is structurally recursive (since it follows the inductive structure of its input) and it passes the unit test:
# test_list_append_int append_v0;;
- : bool = true
#
In the induction step, the let-expression that declares zs, in the definition of visit, is cosmetic and so we can unfold it:
let list_append_v1 xs_given ys_given =
let rec visit xs =
match xs with
| [] ->
ys_given
| x :: xs' ->
x :: visit xs'
in visit xs_given;;
(Again, the expressions let zs = visit xs' in x :: zs and x :: zs are observationally equivalent since in both cases, visit xs' is evaluated first since the arguments of :: are evaluated from right to left.)
This simplified implementation is still structurally recursive and it passes the unit test:
# test_list_append_int list_append_v1;;
- : bool = true
#
Food for thought¶
- When concatenating two lists, the second one ends up as a physical suffix of the result, but that is not verified in the unit-test function above. How could it be verified?
- How could one define a concatenation function where the second list does not end up as a physical suffix of the result?
The following exercise the analogue of the food for thought in Exercise 5, in the chapter about Unit tests, revisited.
Exercise 2¶
Is list concatenation associative?
Does list concatenation admit a neutral element on the left? If so, which one?
Does list concatenation admit a neutral element on the right? If so, which one?
Is list concatenation commutative?
Consider the following definition:
let length_of_concatenation v1s v2s = List.length (v1s @ v2s) = List.length v1s + List.length v2s;;
What is the result of applying length_of_concatenation to any two lists?
- true, always?
- false, always?
- sometimes true, sometimes false?
Justify your answers.
On the right associativity of list concatenation¶
To concatenate three lists, we can either concatenate the two first, and prepend the result to the third, or prepend the first to the result of concatenating the two others.
In that sense, extensionally, the two following definitions are equivalent and list concatenation is associative:
let list_append3_v1 x1s x2s x3s =
x1s @ (x2s @ x3s);;
let list_append3_v2 x1s x2s x3s =
(x1s @ x2s) @ x3s;;
Intensionally, however, the first implementation copies the first list and the second list to construct the result, whereas the second implementation first copies the first list to prepend it to the second, and then copies the result to prepend it to the third list. In effect, the second implementation allocates an auxiliary list for the sole purpose of copying it. This is why @ was declared to be right-associative in OCaml.
Example: duplicating the elements of a list¶
Let us implement a polymorphic function that duplicates the elements of any given list:
let test_list_stutter2_int candidate =
let b0 = (candidate [] = [])
and b1 = (candidate [1] = [1; 1])
and b2 = (candidate [2; 1] = [2; 2; 1; 1])
and b3 = (candidate [3; 2; 1] = [3; 3; 2; 2; 1; 1])
(* etc. *)
in b0 && b1 && b2 && b3;;
The stuttering function is defined following the inductive structure of lists:
base case:
since the empty list contains no elements, there is no element to duplicate and therefore the result should be the empty list
induction step:
for any list vs' whose stuttering yields a list ws (which is the induction hypothesis), making v :: vs' stutter should yield v :: v :: ws
Here is the skeleton of the list-stuttering function:
let list_stutter vs_init =
let rec visit vs =
match vs with
| [] ->
...
| v :: vs' ->
let ws = visit vs'
in ...
in visit vs_init;;
Let us fill the blanks:
in the base case, the result is [], and
in the induction step, the result is obtained by cons’ing v twice to the result of the recursive call:
let list_stutter2 vs_init = let rec visit vs = match vs with | [] -> [] | v :: vs' -> let ws = visit vs' in v :: v :: ws in visit vs_init;;
This implementation is structurally recursive (since it follows the inductive structure of its input) and it passes the unit test:
# test_list_stutter2_int list_stutter2;;
- : bool = true
#
In the induction step, the let-expression that declares ws, in the definition of visit, is cosmetic and so we can unfold it. The simplified implementation also passes the unit test.
Also, the unit-test function provides code coverage because it tests both the base case and the induction step and the implementation is structurally recursive.
Exercise 3¶
Implement a polymorphic function that triplicates the elements of any given list:
let test_list_stutter3_int candidate =
let b0 = (candidate [] = [])
and b1 = (candidate [1] = [1; 1; 1])
and b2 = (candidate [2; 1] = [2; 2; 2; 1; 1; 1])
and b3 = (candidate [3; 2; 1] = [3; 3; 3; 2; 2; 2; 1; 1; 1])
(* etc. *)
in b0 && b1 && b2 && b3;;
Resources¶
- The OCaml code for the present lecture note (latest version: 14 Mar 2020).
Version¶
Fixed a misspelling in “the empty list”, thanks to Syed Muhammad Maaz’s eagle eye [16 Mar 2020]
Aligned the names of the result of each recursive call, after an observation by Yoon Sangho [16 Mar 2020]
Created [14 Mar 2020]