Polymorphic lists in OCaml

The goal of this lecture note is to introduce polymorphic lists in OCaml.

Resources

• The OCaml code for the present lecture note (latest version: 16 Mar 2020).
• The resource file for Listy.cons and Listy.init (latest version: 16 Mar 2020).

Lists

A list is like an onion, with one payload per layer. Like this proverbial onion, it was either constructed with the empty constructor or it was constructed with a pair constructor that holds a list element (the head of the list) and another list (the tail of the list). The list type is predefined in OCaml:

• the empty list is noted [] (and traditionally referred to as “nil”); and

• constructing a value v and a list of values vs is noted v :: vs with the infix operator :: (traditionally referred to as “cons”), and the result of this construction is a new list whose head (i.e., first element) is v and whose tail is vs.

Grammatically:

<type>       ::= ...
               | <type> list

<expression> ::= ...
               | []
               | <expression> :: <expression>

The corresponding typing rules read as follows:

NIL
	G |- [] : t list

CONS	G |- e : t	G |- es : t list
	G |- e :: es : t list

In words:

• in any type environment G, the expression [] has type 'a list (which is the most general type, as we do not know the type of the elements of the empty list, since there isn’t any):

  # [];;
  - : 'a list = []
  #
  

• in any type environment G, the expression e :: es has type t list whenever e has type t and es has type t list, for any type t.

Notationally, lists such as 2 :: (1 :: (0 :: [])) are equivalently written as 2 :: 1 :: 0 :: [], i.e., cons associates to the right. For brevity, OCaml also provides syntactic sugar, in that 2 :: 1 :: 0 :: [] can also be written as [2; 1; 0]. To wit:

# (2 :: (1 :: (0 :: []))) = (2 :: 1 :: 0 :: []);;
- : bool = true
# (2 :: 1 :: 0 :: []) = [2; 1; 0];;
- : bool = true
#

Also, since cons is an OCaml function, its arguments are evaluated from right to left:

# let an_int n = let () = Printf.printf "processing %d...\n" n in n;;
val an_int : int -> int = <fun>
# let the_empty_list () = let () = Printf.printf "processing []...\n" in [];;
val the_empty_list : unit -> 'a list = <fun>
# (an_int 2) :: (the_empty_list ());;
processing []...
processing 2...
- : int list = [2]
#

Lists, in OCaml, are homogeneous but polymorphic: all the elements in a list must have the same type (homogeneity), but there can be lists of elements of any type (polymorphism). To wit, here is the same interaction as above, but with Booleans instead of with integers (polymorphism), and then an ill-fated attempt at constructing a heterogeneous list of integers and Booleans:

# (true :: (true :: (false :: []))) = (true :: true :: false :: []);;
- : bool = true
# (true :: true :: false :: []) = [true; true; false];;
- : bool = true
# 1 :: true :: [];;
Characters 5-9:
  1 :: true :: [];;
       ^^^^
Error: This expression has type bool but an expression was expected of type
         int
#

The “plural” naming convention

The following naming convention is used in the purely functional programming language Haskell:

• Assuming a variable v that denotes a value, the variable denoting a list of values is named vs.
• So if n denotes an integer, a list of integers is denoted by ns, if b denotes a Boolean, a list of Booleans is denoted by bs, etc.
• And yes, a list of list of Booleans is named bss and a list of lists of lists of integers is named nsss (not that there are too many of those in practice, but it is the principle that matters).

This naming convention tends to make programs more readable, understandable, and predictable.

A sample of lists

The following interaction illustrates the naming of the empty list (vs0), of three lists of Booleans (bs1, bs2, and bs3), and of several lists of integers (ns1 and friends):

# let vs0 = [];;
val vs0 : 'a list = []
# let bs1 = [true];;
val bs1 : bool list = [true]
# let bs2 = [false; true];;
val bs2 : bool list = [false; true]
# let bs3 = [false; false; true];;
val bs3 : bool list = [false; false; true]
# let ns1 = [0];;
val ns1 : int list = [0]
# let ns1' = 0 :: vs0;;
val ns1' : int list = [0]
# let ns2 = [1; 0];;
val ns2 : int list = [1; 0]
# let ns2' = 1 :: ns1';;
val ns2' : int list = [1; 0]
# let ns3 = [2; 1; 0];;
val ns3 : int list = [2; 1; 0]
# let ns3' = 2 :: ns2';;
val ns3' : int list = [2; 1; 0]
# let ns4 = [3; 2; 1; 0];;
val ns4 : int list = [3; 2; 1; 0]
# let ns4' = 3 :: ns3';;
val ns4' : int list = [3; 2; 1; 0]
#

In OCaml, unlike in Python, lists are really represented as linked pairs in memory:

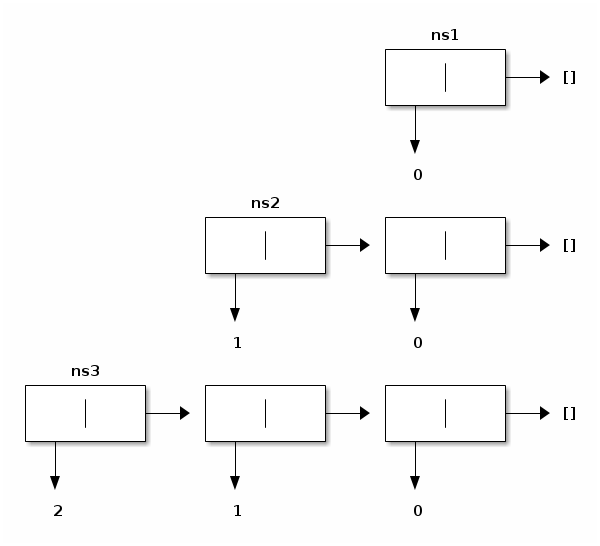
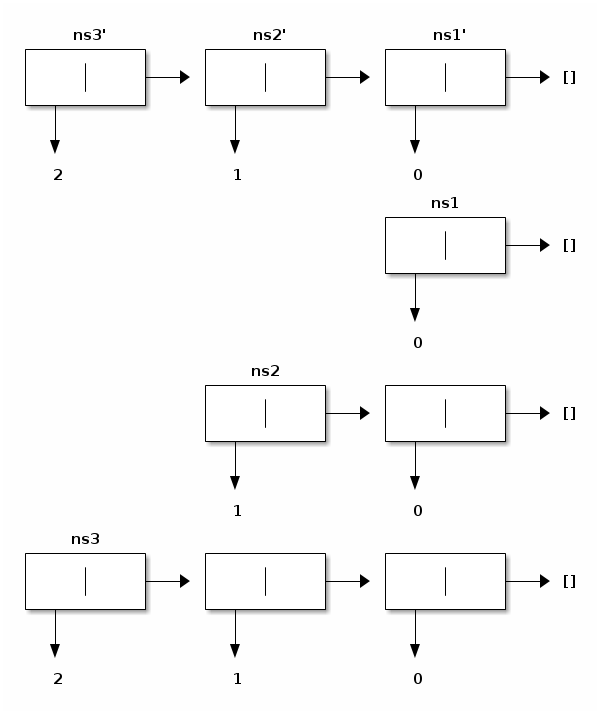
In this depiction, the names ns1, ns2, and ns3 stand above the value they denote. Since these values have been constructed independently, their representation is distinct, unlike the values denoted by ns1', ns2', and ns3', whose representation is shared:

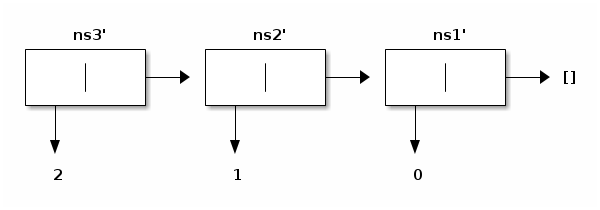
Linguistically, OCaml provides a way to distinguish the values of ns3 and of ns3':

• the infix operator = tests “structural equality” (following the inductive structure of values all the way to atomic values, that are tested for atomic, type-specific equality), and
• the infix operator == tests “physical equality” (identity of internal representations).

For example,

• the denotations of ns3 and of ns3' are structurally equal:

  # ns3 = ns3';;
  - : bool = true
  #
  

• the denotations of ns3 and of ns3' are not physically equal:

  # ns3 == ns3';;
  - : bool = false
  #
  

In the Animal Farm,

all animals are equal,

but some animals are more equal than others.

—George Orwell

The list constructor, in actuality

The infix notation :: stands for the predefined function List.cons, where List. is OCaml’s list library:

# List.cons 2 (List.cons 1 (List.cons 0 [])) = 2 :: 1 :: 0 :: [];;
- : bool = true
# List.cons 2 (List.cons 1 (List.cons 0 []));;
- : int list = [2; 1; 0]
# 2 :: 1 :: 0 :: [];;
- : int list = [2; 1; 0]
# [2; 1; 0];;
- : int list = [2; 1; 0]
#

(If your version of OCaml predates 4.03.0, fear not, download this resource file, and write Listy.cons instead of List.cons.)

Pictorially:

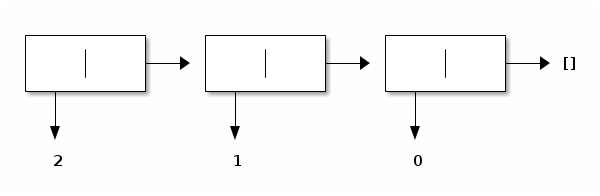
So all in all:

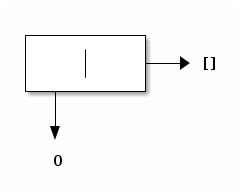
• Given an element (say, 0) and a pre-constructed list (say, the empty list, []), we can construct another list, namely [0]:

  # List.cons 0 [];;
  - : int list = [0]
  # 0 :: [];;
  - : int list = [0]
  #
  

  Pictorially:

  

• Given an element (say, 1) and a pre-constructed list (say, [0]), we can construct another list, namely [1; 0]:

  # List.cons 1 [0];;
  - : int list = [1; 0]
  # 1 :: [0];;
  - : int list = [1; 0]
  #
  

  Pictorially:

  

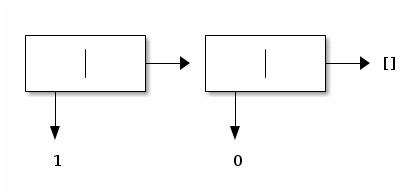
• Given an element (say, 2) and a pre-constructed list (say, [1; 0]), we can construct another list, namely [2; 1; 0]:

  # List.cons 2 [1; 0];;
  - : int list = [2; 1; 0]
  # 2 :: [1; 0];;
  - : int list = [2; 1; 0]
  #
  

  Pictorially:

  

• Given an element (say, 3) and a pre-constructed list (say, [2; 1; 0]), we can construct another list, namely [3; 2; 1; 0]:

  # List.cons 3 [2; 1; 0];;
  - : int list = [3; 2; 1; 0]
  # 3 :: [2; 1; 0];;
  - : int list = [3; 2; 1; 0]
  #
  

  Pictorially:

  

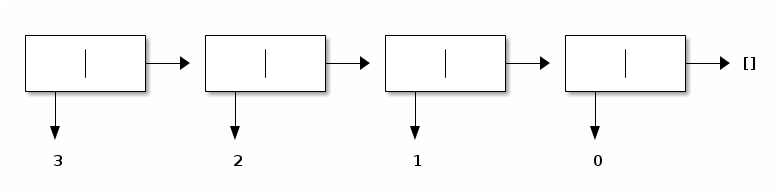
• And given an element (say, 4) and a pre-constructed list (say, [3; 2; 1; 0]), we can construct yet another list, namely [4; 3; 2; 1; 0]:

  # List.cons 4 [3; 2; 1; 0];;
  - : int list = [4; 3; 2; 1; 0]
  # 4 :: [3; 2; 1; 0];;
  - : int list = [4; 3; 2; 1; 0]
  #
  

  Pictorially:

  

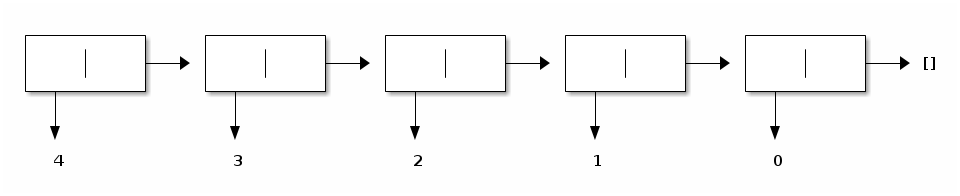
Another term for lists, that is pictorially justified above, is “linked lists”, since the second component of each pair links this pair to the rest of the list. Lists in OCaml, however, are immutable, which means that neither their heads nor their tails can be mutated. (We will study mutable data in not very long. They make it possible to create circular lists, which are a source of interesting problems.) Since lists are immutable, they are constructed inductively (and therefore finite) and list-processing programs are structurally recursive.

Constructing lists: the atoi function

Given a non-negative integer n, the atoi function constructs the list of decreasing integers from n-1 to 0:

let test_atoi candidate =
      (* a few handpicked numbers: *)
  let b0 = (candidate 0 = [])
  and b1 = (candidate 1 = [0])
  and b2 = (candidate 2 = [1; 0])
  and b3 = (candidate 3 = [2; 1; 0])
  and b4 = (candidate 4 = [3; 2; 1; 0])
  (* etc. *)
  in b0 && b1 && b2 && b3 && b4;;

The atoi function is defined following the inductive structure of natural numbers:

• base case (i.e., n = 0): since there is no number between -1 and 0, atoi should map 0 to the empty list
• induction step (i.e., n = succ n’): given a non-negative number n' that atoi maps to the list of decreasing integers from n’-1 to 0 (which is the induction hypothesis), it should map succ n' to a list of decreasing integers from n’ to 0; this list is obtained by cons’ing n’ to the list of decreasing integers from n’-1 to 0

Let us expand the unit-test function with instances of the base case and the induction step:

let test_atoi candidate =
      (* base case: *)
  let bc = (candidate 0 = [])
      (* instance of the induction step: *)
  and is = (let n' = Random.int 10
            in candidate (succ n') = n' :: candidate n')
      (* a few handpicked numbers: *)
  and b1 = (candidate 1 = [0])
  and b2 = (candidate 2 = [1; 0])
  and b3 = (candidate 3 = [2; 1; 0])
  and b4 = (candidate 4 = [3; 2; 1; 0])
  (* etc. *)
  in bc && is && b1 && b2 && b3 && b4;;

Since atoi is specified over non-negative integers, we might as well shield it. Here is its skeleton:

let atoi_v0 n =
  let () = assert (0 <= n)
  in let rec visit n =
       if n = 0
       then ...
       else let n' = n - 1
            in let ih = visit n'
               in ...
     in visit n;;

Rationale:

• the assert-expression ensures that the argument is not a negative integer;
• the skeleton of the recursive function named visit embodies the base case (n denotes 0) and the induction step (n denotes the successor of an integer n’).

Now all we need is to fill the blanks:

• in the base case, the result is [], and

• in the induction step, the result is obtained by cons’ing n' to the result of the recursive call:

  let atoi_v0 n =
    let () = assert (0 <= n) in
    let rec visit n =
      if n = 0
      then []
      else let n' = n - 1
           in let ih = visit n'
              in n' :: ih
    in visit n;;
  

This shielded implementation is structurally recursive and it passes our unit test:

# test_atoi atoi_v0;;
- : bool = true
#

In the induction step, the let-expression that declares ih, in the definition of visit, is cosmetic and so we can unfold it:

let atoi_v1 n =
  let () = assert (0 <= n) in
  let rec visit n =
     if n = 0
     then []
     else let n' = n - 1
          in n' :: visit n'
   in visit n;;

This simplified implementation is still structurally recursive and it passes the unit test:

# test_atoi atoi_v1;;
- : bool = true
#

Food for thought:

In the definition of atoi_v1, the let-expression that declares n' is non-linear since n' occurs twice in its body. Unfolding this let-expression would duplicate the decrement operation:

let atoi_v2 n =
  let () = assert (0 <= n) in
  let rec visit n =
     if n = 0
     then []
     else (n - 1) :: visit (n - 1)
   in visit n;;

This implementation is still structurally recursive and it passes the unit test:

# test_atoi atoi_v2;;
- : bool = true
#

Destructuring non-empty lists: list accessors

Matching the binary structure of non-empty lists, and the arity of the list constructor List.cons (alias Listy.cons), lists are endowed with two canonical accessors: List.hd, to fetch their head, and List.tl, to fetch their tail:

# List.hd (List.cons 10 (List.cons 20 (List.cons 30 [])));;
- : int = 10
# List.tl (List.cons 10 (List.cons 20 (List.cons 30 [])));;
- : int list = [20; 30]
#

Or again, using the ordinary infix notation for constructing lists:

# List.hd (10 :: 20 :: 30 :: []);;
- : int = 10
# List.tl (10 :: 20 :: 30 :: []);;
- : int list = [20; 30]
#

Or yet again, using the shorter representation for lists:

# List.hd [10; 20; 30];;
- : int = 10
# List.tl [10; 20; 30];;
- : int list = [20; 30]
#

List.hd and List.tl expect their argument to be a non-empty list. Otherwise, they raise an exception:

# List.hd [];;
Exception: Failure "hd".
# List.tl [];;
Exception: Failure "tl".
#

Using list accessors, we can test whether sublists are shared. To this end, let us revisit ns1, ns1', ns2, ns2', ns3, and ns3':

let ns1 = [0];;

let ns1' = 0 :: vs0;;

let ns2 = [1; 0];;

let ns2' = 1 :: ns1';;

let ns3 = [2; 1; 0];;

let ns3' = 2 :: ns2'

let ns4 = [3; 2; 1; 0];;

let ns4' = 3 :: ns3';;

Depicting the resulting lists with each name standing above the value it denotes makes it clear how the lists denoted by ns1', ns2', and ns3' are shared, whereas the lists denoted by ns1, ns2, and ns3 are not:

Using the infix operators = (structural equality) and == (physical equality), we can test a series of equalities to detect sharing:

• the tail of the list denoted by ns3 and the denotation of ns2 are structurally equal, but they are not physically equal:

  # List.tl ns3 = ns2;;
  - : bool = true
  # List.tl ns3 == ns2;;
  - : bool = false
  #
  

• the tail of the list denoted by ns3' and the denotation of ns2' are both structurally and physically equal:

  # List.tl ns3' = ns2';;
  - : bool = true
  # List.tl ns3' == ns2';;
  - : bool = true
  #
  

• the tail of the tail of the list denoted by ns3' and the tail of the list denoted by ns2' are both structurally and physically equal:

  # List.tl (List.tl ns3') = List.tl ns2';;
  - : bool = true
  # List.tl (List.tl ns3') == List.tl ns2';;
  - : bool = true
  #
  

Harald: Physical equality implies structural equality, right?

Alfrothul: Right.

Prototypical skeleton of structurally recursive functions over lists

Matching the inductive structure of lists, here is the prototypical skeleton of a structurally recursive function visit that processes a given list:

• with a let-expression naming the result of the recursive call:

  let rec visit vs =
    if vs = []
    then ...
    else let v = List.hd vs
         and vs' = List.tl vs
         in let ih = visit vs'
            in ...ih...;;
  

• without this let expression as well as the let expression naming the tail of the list in the induction step:

  let rec visit vs =
    if vs = []
    then ...
    else let v = List.hd vs
         in ...visit (List.tl vs)...;;
  

Unparsing polymorphic lists

To unparse a list into a string, we need (1) to traverse it recursively and (2) to unparse its elements:

let test_show_int_list candidate =
  let b0 = (candidate []
            = "[]")
  and b1 = (candidate [0]
            = "0 :: []")
  and b2 = (candidate [1; 0]
            = "1 :: 0 :: []")
  and b3 = (candidate [2; 1; 0]
            = "2 :: 1 :: 0 :: []")
  and b4 = (candidate [~-2; ~-1; 0]
            = "~-2 :: ~-1 :: 0 :: []")
  (* etc. *)
  in b0 && b1 && b2 && b3 && b4;;

let test_show_bool_list candidate =
  let b0 = (candidate []
            = "[]")
  and b1 = (candidate [false]
            = "false :: []")
  and b2 = (candidate [true; false]
            = "true :: false :: []")
  and b3 = (candidate [true; true; false]
            = "true :: true :: false :: []")
  (* etc. *)
  in b0 && b1 && b2 && b3;;

let test_show_int_list_list candidate =
  let b0 = (candidate [[]]
            = "[] :: []")
  and b1 = (candidate [[0]]
            = "(0 :: []) :: []")
  and b2 = (candidate [[1; 0]; [0]]
            = "(1 :: 0 :: []) :: (0 :: []) :: []")
  and b3 = (candidate [[2; 1; 0]; [1; 0]; [0]]
            = "(2 :: 1 :: 0 :: []) :: (1 :: 0 :: []) :: (0 :: []) :: []")
  and b4 = (candidate [[3; 2; 1; 0]; [2; 1; 0]; [1; 0]; [0]]
            = "(3 :: 2 :: 1 :: 0 :: []) :: (2 :: 1 :: 0 :: []) :: (1 :: 0 :: []) :: (0 :: []) :: []")
  and b5 = (candidate [[~-2; ~-1; 0]; [3; 2; 1; 0]; [2; 1; 0]; [1; 0]; [0]]
            = "(~-2 :: ~-1 :: 0 :: []) :: (3 :: 2 :: 1 :: 0 :: []) :: (2 :: 1 :: 0 :: []) :: (1 :: 0 :: []) :: (0 :: []) :: []")
  (* etc. *)
  in b0 && b1 && b2 && b3 && b4 && b5;;

(Note how we need to write separate unit-test functions for each of them to be well typed.)

Formally, following the structure of lists leads us to specifying the function inductively as follows, given an unparsing function for the list elements:

• base case: the unparsed counterpart of the empty list is []
• induction step: given a list vs' such that uvs' is its unparsed counterpart (which is the induction hypothesis), and given a list element v, the unparsed counterpart of v :: vs' is obtained by concatenating (1) the unparsed counterpart of v, (2) the string " :: ", and (3) uvs'

Here is the skeleton of the list-unparsing function:

let show_list show_yourself vs_given =
  let rec show_list_aux vs =
    if vs = []
    then ...
    else let v = List.hd vs
         and vs' = List.tl vs
         in let uvs' = show_list_aux vs'
            in ...
  in show_list_aux vs_given;;

Rationale:

• show_list is parameterized with another unparsing function, show_yourself, to unparse the list elements;
• the skeleton of visit follows the inductive structure of lists, i.e., it has a base case (the argument is the empty list) and an induction step (the argument is not the empty list).

Now all we need is to fill the blanks:

• in the base case, the result is "[]", and

• in the induction step, the result is obtained by concatenating the unparsed counterpart of v (obtained by applying show_yourself), the string " :: ", and the result of the recursive call:

  let show_list show_yourself vs_given =
    let rec show_list_aux vs =
      if vs = []
      then "[]"
      else let v = List.hd vs
           and vs' = List.tl vs
           in let uvs' = show_list_aux vs'
              in (show_yourself v) ^ " :: " ^ uvs'
    in show_list_aux vs_given;;
  

This implementation is structurally recursive (since it follows the inductive structure of its input) and, assuming the unparsing functions for integers (show_int) and Booleans (show_bool) from Week 05, it passes the two first unit tests:

# test_show_int_list (show_list show_int);;
- : bool = true
# test_show_bool_list (show_list show_bool);;
- : bool = true
#

However, it does not pass the unit test for nested lists because of its expected parentheses:

# test_show_int_list_list (show_list (show_list show_int));;
- : bool = false
#

To this end, we need an auxiliary function that inserts these parentheses when the given list is nonempty:

let show_listp show_yourself vs =
  if vs = []
  then "[]"
  else "(" ^ show_list show_yourself vs ^ ")";;

Thus equipped, the unit-test function for nested lists is satisfied:

# test_show_int_list_list (show_list (show_listp show_int));;
- : bool = true
#

The atoi function, revisited

We are now equipped to program a traced version of atoi, to visualize the construction of the resulting list:

let traced_atoi_v0 n =
  let () = Printf.printf "atoi_v0 %d ->\n" n in
  let () = assert (n >= 0)
  in let rec visit n i =
       let () = Printf.printf "%svisit %d ->\n" (indent i) n in
       let result = if n = 0
                    then []
                    else let n' = pred n
                         in let ih = visit n' (i + 1)
                            in n' :: ih
       in let () = Printf.printf "%svisit %d <- %s\n" (indent i) n (show_list show_int result) in
          result
     in let final_result = visit n 1
        in let () = Printf.printf "atoi_v0 %d <- %s\n" n (show_list show_int final_result) in
           final_result;;

Specifically,

• when traced_atoi_v0 is called on a number n, it emits the trace atoi_v0 n ->,
• when traced_atoi_v0 n returns a result result, it emits the trace atoi_v0 n <- result,
• when visit is called on a number n, it emits the trace visit n ->, and
• when visit n returns a result result, it emits the trace visit n <- result.

In addition,

• each call is indented proportionally to its nesting, and
• each return has the same indentation as the corresponding call.

To wit:

# traced_atoi_v0 5;;
atoi_v0 5 ->
  visit 5 ->
    visit 4 ->
      visit 3 ->
        visit 2 ->
          visit 1 ->
            visit 0 ->
            visit 0 <- []
          visit 1 <- 0 :: []
        visit 2 <- 1 :: 0 :: []
      visit 3 <- 2 :: 1 :: 0 :: []
    visit 4 <- 3 :: 2 :: 1 :: 0 :: []
  visit 5 <- 4 :: 3 :: 2 :: 1 :: 0 :: []
atoi_v0 5 <- 4 :: 3 :: 2 :: 1 :: 0 :: []
- : int list = [4; 3; 2; 1; 0]
#

The trace visualizes how each call to any number succ n' triggers a recursive call to n', and how the corresponding return (which is vertically aligned with the corresponding call) cons’es n' to the resulting list.

Incidentally, it is simple to change the indentation: just redefine indent in the resource file and load it again. For example, if one wants to indent with not twice the number of nested calls, but 5 times, one changes 2 into 5 in the definition of indent:

let indent i =
  String.make (5 * i) ' ';;

Loading the file then yields the following trace:

# traced_atoi_v0 5;;
atoi_v0 5 ->
     visit 5 ->
          visit 4 ->
               visit 3 ->
                    visit 2 ->
                         visit 1 ->
                              visit 0 ->
                              visit 0 <- []
                         visit 1 <- 0 :: []
                    visit 2 <- 1 :: 0 :: []
               visit 3 <- 2 :: 1 :: 0 :: []
          visit 4 <- 3 :: 2 :: 1 :: 0 :: []
     visit 5 <- 4 :: 3 :: 2 :: 1 :: 0 :: []
atoi_v0 5 <- 4 :: 3 :: 2 :: 1 :: 0 :: []
- : int list = [4; 3; 2; 1; 0]
#

Alfrothul: Man, 5 is the perfect number here.

Harald: Yes, it just fits.

Vigfus: Er... What just fits?

Alfrothul: The right alignment of the values visit returns.

Loki: Thanks the gods for monospaced fonts.

The indentation is larger, which might make it clearer how each call and its corresponding return are vertically aligned.

About the nesting in the traces

Incidentally, and as pointed out by Dijkstra in 1960, the nesting in the traces is accurately modeled with a stack of plates, that starts empty and where plates are successively pushed on top and then successively popped from the top. And indeed calls and returns are implemented in OCaml with such a stack, the control stack. OCaml’s control stack occupies a finite area in memory, and when this area proves too small, the computation is interrupted and a “stack overflow” error message is issued:

# let rec diverge () = not (diverge ()) in diverge ();;
Stack overflow during evaluation (looping recursion?).
#

In contrast, in a system such as Chez Scheme, the control stack grows on demand, because who is the implementer to set a limit to the computing needs of their users, and as a result, a diverging computation elicits a system error. In the Coq proof assistant, which is implemented in OCaml, the control stack occupies a much larger area of memory.

As for the semiotics of the error message Stack overflow during evaluation (looping recursion?).,

Interlude

Harald: That’s our cue.

Alfrothul: Semioticists of all countries, unite.

Umberto Eco: Do you guys need a chairperson by any chance?

Mimer: Prof. Eco, thanks for stopping by! I simply love your book of collected articles “To say almost the same, experiments in translation” (i.e., the French edition of “Dire quasi la stessa cosa, esperienze di traduzione”, it doesn’t seem to exist in English) about translating from one natural language to another. A lot of it directly applies to designing compilers for programming languages, it’s so striking.

Harald: Er... We are talking about semiotics or what?

Mimer: Sorry. Youthful enthusiasm and all that. This figment of imagination felt too good to let it pass by. And yes, I do know that Umberto Eco has already passed away.

Alfrothul (kindly): You can still read his books.

Harald: Er... Semiotics, anyone?

Vigfus (jumping in): Right. If it’s a loop, the control stack shouldn’t overflow, should it?

Brynja: Indeed. In a functional language, iteration is implemented by tail recursion, and looping is an unbounded iteration.

Loki (virtuously): Right. Tail recursion is its own reward. That’s semiotics for you.

Harald: Well, yes, but Brynja’s point does hold.

Loki: Are we arguing semiotics or semantics now?

Alfrothul: Kind of. Look at these interludes, for example. Are they allegorical or metaphorical?

Robin Milner (the voice of wisdom): You guys are quite the purists. That’s not necessarily a bad thing, but how about getting back to unparsing polymorphic lists? Because the show must go on. Unless you need a chairperson perhaps?

Mimer: Prof. Milner, thanks for stopping by! And thanks too for ML.

Harald (to Alfrothul): More youthful enthusiasm, seems like.

Halcyon (unfazed): So we won’t get to talk about Umberto Eco’s treatise The Infinity of Lists? It looks on topic.

Mimer: Not yet, but we will look at infinite lists soon.

Vigfus: In OCaml? No way.

Robin Milner (kindly): Ahem.

Unparsing polymorphic lists, refined

In practice, we’d rather see [1; 2; 3] in traces, not 1 :: 2 :: 3 :: [], because that is how OCaml prints list. And indeed a trace for atoi such as the following one is more readable than the traces displayed above:

# traced_atoi_v0 5;;
atoi_v0 5 ->
  visit 5 ->
    visit 4 ->
      visit 3 ->
        visit 2 ->
          visit 1 ->
            visit 0 ->
            visit 0 <- []
          visit 1 <- [0]
        visit 2 <- [1; 0]
      visit 3 <- [2; 1; 0]
    visit 4 <- [3; 2; 1; 0]
  visit 5 <- [4; 3; 2; 1; 0]
atoi_v0 5 <- [4; 3; 2; 1; 0]
- : int list = [4; 3; 2; 1; 0]
#

Let us go back to the starting point. To unparse a list into a string, we need (1) to traverse it recursively and (2) to unparse its elements:

let test_show_int_list candidate =
  let b0 = (candidate []
            = "[]")
  and b1 = (candidate [0]
            = "[0]")
  and b2 = (candidate [1; 0]
            = "[1; 0]")
  and b3 = (candidate [2; 1; 0]
            = "[2; 1; 0]")
  and b4 = (candidate [~-2; ~-1; 0]
            = "[~-2; ~-1; 0]")
  (* etc. *)
  in b0 && b1 && b2 && b3 && b4;;

let test_show_bool_list candidate =
  let b0 = (candidate []
            = "[]")
  and b1 = (candidate [false]
            = "[false]")
  and b2 = (candidate [true; false]
            = "[true; false]")
  and b3 = (candidate [true; true; false]
            = "[true; true; false]")
  (* etc. *)
  in b0 && b1 && b2 && b3;;

let test_show_int_list_list candidate =
  let b0 = (candidate [[]]
            = "[[]]")
  and b1 = (candidate [[0]]
            = "[[0]]")
  and b2 = (candidate [[1; 0]; [0]]
            = "[[1; 0]; [0]]")
  and b3 = (candidate [[2; 1; 0]; [1; 0]; [0]]
            = "[[2; 1; 0]; [1; 0]; [0]]")
  and b4 = (candidate [[3; 2; 1; 0]; [2; 1; 0]; [1; 0]; [0]]
            = "[[3; 2; 1; 0]; [2; 1; 0]; [1; 0]; [0]]")
  and b5 = (candidate [[~-2; ~-1; 0]; [3; 2; 1; 0]; [2; 1; 0]; [1; 0]; [0]]
            = "[[~-2; ~-1; 0]; [3; 2; 1; 0]; [2; 1; 0]; [1; 0]; [0]]")
  (* etc. *)
  in b0 && b1 && b2 && b3 && b4 && b5;;

The first version of unparsing function is not the one we are looking for, since we want to obtain, e.g., [2; 1; 0], not "2 :: 1 :: 0 :: []".

To this end, we need a BNF of bracketed lists with infix separators.

Here is one:

<bracketed-list>                    ::= [ <remnant-of-bracketed-list>

<remnant-of-bracketed-list>         ::= ]
                                      | <list-element> <tail-of-remnant-of-bracketed-list>

<tail-of-remnant-of-bracketed-list> ::= ]
                                      | ; <list-element> <tail-of-remnant-of-bracketed-list>

This grammar captures the fact that the infix ; occurs after each element of the list, except the last one.

Examples:

• The following derivation gives the empty list:

  <bracketed-list> ->
  [ <remnant-of-bracketed-list> ->
  [ ]
  

• The following derivation gives a singleton list (picking 10 as a list element):

  <bracketed-list> ->
  [ <remnant-of-bracketed-list> ->
  [ <list-element> <tail-of-remnant-of-bracketed-list> ->
  [ 10 <tail-of-remnant-of-bracketed-list> ->
  [ 10 ]
  

• The following derivation gives a list of 2 elements (picking 10 and 20 as these elements):

  <bracketed-list> ->
  [ <remnant-of-bracketed-list> ->
  [ <list-element> <tail-of-remnant-of-bracketed-list> ->
  [ 10 <tail-of-remnant-of-bracketed-list> ->
  [ 10 ; <list-element> <tail-of-remnant-of-bracketed-list> ->
  [ 10 ; 20 <tail-of-remnant-of-bracketed-list> ->
  [ 10 ; 20 ]
  

• The following derivation gives a list of 3 elements (picking 10, 20, and 30 as these elements):

  <bracketed-list> ->
  [ <remnant-of-bracketed-list> ->
  [ <list-element> <tail-of-remnant-of-bracketed-list> ->
  [ 10 <tail-of-remnant-of-bracketed-list> ->
  [ 10 ; <list-element> <tail-of-remnant-of-bracketed-list> ->
  [ 10 ; 20 <tail-of-remnant-of-bracketed-list> ->
  [ 10 ; 20 ; <list-element> <tail-of-remnant-of-bracketed-list> ->
  [ 10 ; 20 ; 30 <tail-of-remnant-of-bracketed-list> ->
  [ 10 ; 20 ; 30 ]
  

We can convince ourselves of the soundness and completeness of this grammar:

• Soundness:

  Using the grammar as a generator, we can only construct well-bracketed and well-infixed representation of lists.

• Completeness:

  Any well-bracketed and well-infixed representation of lists can be obtained by a derivation using this grammar.

Concretely, we are special-casing the empty list at the outset and inductively specifying an auxiliary unparsing function over the tail of non-empty lists, given an unparsing function for the list elements:

• base case:

  finishing to unparse the empty list yields "]"

• induction step:

  given a list vs' such that uvs' is the result of finishing to unparse vs' (which is the induction hypothesis), and given a list element v, finishing to unparse v :: vs' is obtained by concatenating (1) the separator "; ", (2) the unparsed counterpart of v, and (3) uvs'

At the outset, the unparsed counterpart of the empty list is the concatenation of "[" and "]", and the unparsed counterpart of a non-empty list v :: vs' is the concatenation of "[", the unparsed counterpart of v, and the result of finishing to unparse vs as specified just above.

In OCaml, this unparsing function is implemented as a structurally recursive function mapping a list to a string. Since lists in OCaml are polymorphic, we parameterize their unparsing function with an unparsing function for the elements of the given lists:

let show_list show_yourself vs_init =
  if vs_init = []
  then "[]"
  else let v = List.hd vs
       and vs' = List.tl vs
       in let rec show_list_aux vs v =
            if vs = []
            then show_yourself v
            else let v' = List.hd vs
                 and vs' = List.tl vs
                 in let uvs' = show_list_aux vs' v'
                    in (show_yourself v) ^ "; " ^ uvs'
          in "[" ^ (show_list_aux vs' v) ^ "]";;

Analysis:

• at the outset, the main function (which is not recursive) distinguishes between empty and non-empty list,
• the auxiliary function (which is (structurally) recursive) follows the inductive structure of its second argument; in particular, its recursive call implements the induction hypothesis.

This OCaml function passes the unit tests:

# test_show_int_list (show_list show_int);;
- : bool = true
# test_show_bool_list (show_list show_bool);;
- : bool = true
# test_show_int_list_list (show_list (show_list show_int));;
- : bool = true
#

The atoi function, re2visited

And now traced_atoi_v0 emits traces with the bracketed notation for lists, as wished for.

Another interlude

Vigfus: So what would be the right indentation now to obtain the vertical alignment on the right due to the monospaced font?

Alfrothul (munching his lower lip): Lemmesee... <clickety clickety click> I’d say 4. C-c C-b:

# traced_atoi_v0 9;;
atoi_v0 9 ->
   visit 9 ->
      visit 8 ->
         visit 7 ->
            visit 6 ->
               visit 5 ->
                  visit 4 ->
                     visit 3 ->
                        visit 2 ->
                           visit 1 ->
                              visit 0 ->
                              visit 0 <- []
                           visit 1 <- [0]
                        visit 2 <- [1; 0]
                     visit 3 <- [2; 1; 0]
                  visit 4 <- [3; 2; 1; 0]
               visit 5 <- [4; 3; 2; 1; 0]
            visit 6 <- [5; 4; 3; 2; 1; 0]
         visit 7 <- [6; 5; 4; 3; 2; 1; 0]
      visit 8 <- [7; 6; 5; 4; 3; 2; 1; 0]
   visit 9 <- [8; 7; 6; 5; 4; 3; 2; 1; 0]
atoi_v0 9 <- [8; 7; 6; 5; 4; 3; 2; 1; 0]
- : int list = [8; 7; 6; 5; 4; 3; 2; 1; 0]
#

Harald: Yup.

Vigfus: Right, but that only works until 9.

Harald: Compound unparsing, here we come.

Compound unparsing

So now we can unparse arbitrary values by following the structure of their type:

• for example, we can unparse lists of pairs:

  # show_list (show_pair show_int show_bool);;
  - : (int * bool) list -> string = <fun>
  # show_list (show_pair show_int show_bool) [];;
  - : string = "[]"
  # show_list (show_pair show_int show_bool) [(3, true)];;
  - : string = "[(3, true)]"
  # show_list (show_pair show_int show_bool) [(3, true); (2, false)];;
  - : string = "[(3, true); (2, false)]"
  # show_list (show_pair show_int show_bool) [(3, true); (2, false); (1, false)];;
  - : string = "[(3, true); (2, false); (1, false)]"
  #
  

• and we can unparse pairs of lists:

  # show_pair (show_list show_int) (show_list show_bool);;
  - : int list * bool list -> string = <fun>
  # show_pair (show_list show_int) (show_list show_bool) ([], []);;
  - : string = "([], [])"
  # show_pair (show_list show_int) (show_list show_bool) ([3], []);;
  - : string = "([3], [])"
  # show_pair (show_list show_int) (show_list show_bool) ([2; 3], []);;
  - : string = "([2; 3], [])"
  # show_pair (show_list show_int) (show_list show_bool) ([2; 3], [true]);;
  - : string = "([2; 3], [true])"
  # show_pair (show_list show_int) (show_list show_bool) ([2; 3], [false; true]);;
  - : string = "([2; 3], [false; true])"
  #
  

Food for thought:

• How would we unparse lists of triples?
• How would we unparse triples of lists?

Further food for thought:

• How would we unparse lists of lists of booleans?
• How would we unparse lists of lists of lists of integers?
• How would we unparse lists of lists of lists of triples of integers, booleans, and characters?

Example: computing the length of a list

Say that we want to count how many elements occur in a list, i.e., its length:

let test_list_length_int candidate =
      (* a few handpicked lists: *)
  let b0 = (0 = candidate [])
  and b1 = (1 = candidate [1])
  and b2 = (2 = candidate [2; 1])
  and b3 = (3 = candidate [3; 2; 1])
  and b4 = (4 = candidate [4; 3; 2; 1])
  (* etc. *)
  in b0 && b1 && b2 && b3 && b4;;

Realizing that atoi maps a number n to a list of length n, we can beef up our unit-test function as follows:

let test_list_length_int candidate =
      (* a few handpicked lists: *)
  let b0 = (0 = candidate [])
  and b1 = (1 = candidate [1])
  and b2 = (2 = candidate [2; 1])
  and b3 = (3 = candidate [3; 2; 1])
  and b4 = (4 = candidate [4; 3; 2; 1])
      (* a few automatically generated lists: *)
  and b5 = (candidate (atoi_v0 5) = 5)
  and b6 = (candidate (atoi_v0 10) = 10)
  and b7 = (candidate (atoi_v0 100) = 100)
  (* etc. *)
  in b0 && b1 && b2 && b3 && b4 && b5 && b6 && b7;;

OCaml provides such a predefined length function, List.length. For the sake of sanity, let us test this unit-test function with this witness function:

# test_list_length_int List.length;;
- : bool = true
#

The length function is defined following the inductive structure of lists:

• base case: the empty list has length 0
• induction step: given a list vs' of length n’ (which is the induction hypothesis), cons-ing an element on top of this list yields a list of length n’+1

And now we can beef up its unit-test function:

let test_list_length_int candidate =
      (* the base case: *)
  let bc = (candidate [] = 0)
      (* instance of the induction step: *)
  and is = (let n = Random.int 1000
            in let ns = atoi_v0 n
               in candidate (n :: ns) = succ (candidate ns))
      (* a few handpicked lists: *)
  and b1 = (1 = candidate [1])
  and b2 = (2 = candidate [2; 1])
  and b3 = (3 = candidate [3; 2; 1])
  and b4 = (4 = candidate [4; 3; 2; 1])
      (* a few automatically generated lists: *)
  and b5 = (candidate (atoi_v0 5) = 5)
  and b6 = (candidate (atoi_v0 10) = 10)
  and b7 = (candidate (atoi_v0 100) = 100)
  (* etc. *)
  in bc && is && b1 && b2 && b3 && b4 && b5 && b6 && b7;;

In OCaml:

let list_length_v0 vs =
 (* list_length_v0 : 'a list -> int *)
  let rec visit vs =
    if vs = []
    then 0
    else let v = List.hd vs
         and vs' = List.tl vs
         in let ih = visit vs'
            in succ ih
  in visit vs;;

This OCaml function passes the unit test:

# test_list_length_int list_length_v0;;
- : bool = true
#

To simplify its definition, we can unfold

• the let expression declaring v because List.hd vs is a pure expression (since vs denotes a non-empty list) and v is unused,

• the let-expression declaring vs' because it is linear and List.tl vs is a pure expression (since vs denotes a non-empty list), and

• the let-expression declaring ih because it is linear and ih is immediately used:

  let list_length_v1 vs =
    let rec visit vs =
      if vs = []
      then 0
      else succ (visit (List.tl vs))
    in visit vs;;
  

This simplified OCaml function passes the unit test:

# test_list_length_int list_length_v1;;
- : bool = true
#

Let us program a traced version of length, to visualize the traversal of the input list:

let traced_list_length_v0 show_yourself vs =
 (* traced_list_length_v0 : ('a -> string) -> 'a list -> int *)
  let () = Printf.printf "list_length_v0 %s ->\n" (show_list show_yourself vs) in
  let rec visit vs i =
    let () = Printf.printf "%svisit %s ->\n" (indent i) (show_list show_yourself vs) in
    let result = if vs = []
                 then 0
                 else let v = List.hd vs
                      and vs' = List.tl vs
                      in let ih = visit vs' (i + 1)
                         in succ ih
       in let () = Printf.printf "%svisit %s <- %d\n" (indent i) (show_list show_yourself vs) result in
          result
    in let final_result = visit vs 1
       in let () = Printf.printf "list_length_v0 %s <- %d\n" (show_list show_yourself vs) final_result in
          final_result;;

Specifically,

• when traced_list_length_v0 is called on a number n, it emits the trace list_length_v0 n ->,
• when traced_list_length_v0 n returns a result result, it emits the trace list_length_v0 n <- result,
• when visit is called on a list vs, it emits the trace visit vs ->, and
• when visit vs returns a result result, it emits the trace visit vs <- result.

In addition,

• each call is indented proportionally to its nesting, and
• each return has the same indentation as the corresponding call.

Also, this tracing function is generic in that it is parameterized with the unparsing function corresponding to the type of elements in the given list:

# traced_list_length_v0 show_int [1; 2; 3; 4; 5];;
list_length_v0 [1; 2; 3; 4; 5] ->
  visit [1; 2; 3; 4; 5] ->
    visit [2; 3; 4; 5] ->
      visit [3; 4; 5] ->
        visit [4; 5] ->
          visit [5] ->
            visit [] ->
            visit [] <- 0
          visit [5] <- 1
        visit [4; 5] <- 2
      visit [3; 4; 5] <- 3
    visit [2; 3; 4; 5] <- 4
  visit [1; 2; 3; 4; 5] <- 5
list_length_v0 [1; 2; 3; 4; 5] <- 5
- : int = 5
# traced_list_length_v0 show_string ["1"; "2"; "3"; "4"; "5"];;
list_length_v0 ["1"; "2"; "3"; "4"; "5"] ->
  visit ["1"; "2"; "3"; "4"; "5"] ->
    visit ["2"; "3"; "4"; "5"] ->
      visit ["3"; "4"; "5"] ->
        visit ["4"; "5"] ->
          visit ["5"] ->
            visit [] ->
            visit [] <- 0
          visit ["5"] <- 1
        visit ["4"; "5"] <- 2
      visit ["3"; "4"; "5"] <- 3
    visit ["2"; "3"; "4"; "5"] <- 4
  visit ["1"; "2"; "3"; "4"; "5"] <- 5
list_length_v0 ["1"; "2"; "3"; "4"; "5"] <- 5
- : int = 5
# traced_list_length_v0 (show_list show_string) [["1"]; ["2"]; ["3"]; ["4"]; ["5"]];;
list_length_v0 [["1"]; ["2"]; ["3"]; ["4"]; ["5"]] ->
  visit [["1"]; ["2"]; ["3"]; ["4"]; ["5"]] ->
    visit [["2"]; ["3"]; ["4"]; ["5"]] ->
      visit [["3"]; ["4"]; ["5"]] ->
        visit [["4"]; ["5"]] ->
          visit [["5"]] ->
            visit [] ->
            visit [] <- 0
          visit [["5"]] <- 1
        visit [["4"]; ["5"]] <- 2
      visit [["3"]; ["4"]; ["5"]] <- 3
    visit [["2"]; ["3"]; ["4"]; ["5"]] <- 4
  visit [["1"]; ["2"]; ["3"]; ["4"]; ["5"]] <- 5
list_length_v0 [["1"]; ["2"]; ["3"]; ["4"]; ["5"]] <- 5
- : int = 5
#

After hours

Vigfus (munching his lower lip): Lemmesee... It will only work for single-digit integers, but <clickety clickety click> maybe 3? C-c C-b:

# traced_list_length_v0 show_int [8; 7; 6; 5; 4; 3; 2; 1];;
list_length_v0 [8; 7; 6; 5; 4; 3; 2; 1] ->
   visit [8; 7; 6; 5; 4; 3; 2; 1] ->
      visit [7; 6; 5; 4; 3; 2; 1] ->
         visit [6; 5; 4; 3; 2; 1] ->
            visit [5; 4; 3; 2; 1] ->
               visit [4; 3; 2; 1] ->
                  visit [3; 2; 1] ->
                     visit [2; 1] ->
                        visit [1] ->
                           visit [] ->
                           visit [] <- 0
                        visit [1] <- 1
                     visit [2; 1] <- 2
                  visit [3; 2; 1] <- 3
               visit [4; 3; 2; 1] <- 4
            visit [5; 4; 3; 2; 1] <- 5
         visit [6; 5; 4; 3; 2; 1] <- 6
      visit [7; 6; 5; 4; 3; 2; 1] <- 7
   visit [8; 7; 6; 5; 4; 3; 2; 1] <- 8
list_length_v0 [8; 7; 6; 5; 4; 3; 2; 1] <- 8
- : int = 8
#

Vigfus: Yup, that’s a match.

Mimer: Funny you should say that.

Destructuring lists conditionally: match expressions

In a typical situation where vs denotes a list, one would check its base case and its induction step:

if vs = []
then ...
else let v = List.hd vs
     and vs' = List.tl vs
     in ...

In the else branch, the list denoted by vs is non-empty and therefore has been constructed with List.cons (alias Listy.cons). We then declare v to denote the head of this list and vs' to denote its tail.

OCaml offers syntactic sugar to express this programming pattern, match-expressions:

match vs with
| [] -> ...
| v :: vs' -> ...

This particular match-expression means exactly the same as the if-expression just above, but it is more convenient to use.

The match-notation scales to distinguishing literals:

let show_int_in_English n =
  match n with
  | 0 ->
     "zero"
  | 1 ->
     "one"
  | -1 ->
     "minus one"
  | 2 ->
     "two"
  | -2 ->
     "minus two"
  | _ ->    (* <-- underscore matches any other value *)
     "too bad";;

To wit:

# show_int_in_English 0;;
- : string = "zero"
# show_int_in_English 1;;
- : string = "one"
# show_int_in_English 2;;
- : string = "two"
# show_int_in_English 3;;
- : string = "too bad"
#

So all in all, the language of expressions of OCaml also features match-expressions:

<expression>    ::= ...
                  | match <expression> with <match-clauses>

<match-clauses> ::= <vertical-bar> <match-clause>
                  | <vertical-bar> <match-clause> <match-clauses>

<vertical-bar>  ::= |

<match-clause>  ::= <pattern> -> <expression>

<pattern>       ::= <formal>

using an artificial non-terminal to distinguish (i.e., disambiguate) the object-level | in a match-expression and the meta-level | in the BNF.

A series of points:

• Unary clauses: match e1 with x -> e2 can also be written match e1 with | x -> e2.

• Unary clauses: match e1 with x -> e2 is equivalent to let x = e1 in e2.

• Each of the expressions in the clauses must have the same type: this type is the type of the match-expression.

• A match-expression is evaluated by first evaluating its first sub-expression, and then by successively “pattern-matching” each pattern in the following sequence of clauses against the resulting value. The first pattern that “matches” the resulting value makes the evaluation of the match-expression reduce to the evaluation of the expression in the clause whose pattern first matched.

  So for example, a nested conditional expression such as:

  if x = 'a'
  then 'A'
  else if x = 'b'
       then 'B'
       else if x = 'c'
            then 'C'
            else assert false
  

  can be more succinctly written as:

  match x with
  | 'a' ->
     'A'
  | 'b' ->
     'B'
  | 'c' ->
     'C'
  | _ ->
     assert false
  

• “Pattern-matching” a pattern against a value means checking whether the structure of the pattern is compatible with the structure of the value. In the example just above, pattern-matching reduces to checking equality. But the pattern may also contain a name (i.e., identifier, or again variable). This name is then bound to the corresponding value, and the expression in the clause is evaluated in an environment that is extended with this binding.

  So for example, a nested conditional expression such as:

  if x = 'a'
  then 'A'
  else if x = 'b'
       then 'B'
       else if x = 'c'
            then 'C'
            else x
  

  can be either written as:

  match x with
  | 'a' ->
     'A'
  | 'b' ->
     'B'
  | 'c' ->
     'C'
  | _ ->
     x
  

  or as:

  match x with
  | 'a' ->
     'A'
  | 'b' ->
     'B'
  | 'c' ->
     'C'
  | y ->
     y
  

  In the last clause, y is bound to the value of x.

  For another example, a let-expression such as:

  let (a, b) = ...
  in a + b
  

  can be written as:

  match ... with
  | (a, b) ->
     a + b
  

• Smartly, the OCaml parser checks the structure of the patterns in match-clauses, and it issues a warning if they do not completely account for the value to be matched or if they are redundant.

  • Example of incompleteness:

    # match 0 with | 0 -> "0";;
    Characters 0-23:
      match 0 with | 0 -> "0";;
      ^^^^^^^^^^^^^^^^^^^^^^^
    Warning 8: this pattern-matching is not exhaustive.
    Here is an example of a value that is not matched:
    1
    - : string = "0"
    #
    

    Non-exhaustive patterns induce run-time errors:

    # match 1 with | 0 -> "0";;
    Characters 0-23:
      match 1 with | 0 -> "0";;
      ^^^^^^^^^^^^^^^^^^^^^^^
    Warning 8: this pattern-matching is not exhaustive.
    Here is an example of a value that is not matched:
    1
    Exception: Match_failure ("//toplevel//", 660, -134).
    #
    

    Non-exhaustive patterns are therefore prohibited here.

  • Example of redundancy:

    # match 0 with | 0 -> "foo" | 0 -> "bar" | _ -> "baz";;
    Characters 28-29:
      match 0 with | 0 -> "foo" | 0 -> "bar" | _ -> "baz";;
                                  ^
    Warning 11: this match case is unused.
    - : string = "foo"
    #
    

    Redundant patterns are therefore prohibited here. There are no pleonasms in OCaml.

Exercise 0

1. Implement an OCaml function of type 'a list -> bool that tests whether its argument is the empty list, using a match-expression.
2. Implement an OCaml function of type 'a list -> bool that tests whether its argument is the empty list, without using a match-expression.
3. Implement an OCaml function of type 'a list -> bool that tests whether its argument is a non-empty list, using a match-expression.
4. Implement an OCaml function of type 'a list -> bool that tests whether its argument is a non-empty list, without using a match-expression.

Prototypical skeleton of structurally recursive functions over lists, revisited

Matching the inductive structure of lists, here is the prototypical skeleton of a structurally recursive function visit that processes a given list:

• with a let-expression naming the result of the recursive call:

  let rec visit vs =
    match vs with
    | [] ->
       ...
    | v :: vs' ->
       let ih = visit vs'
       in ...ih...;;
  

• without this let expression:

  let rec visit vs =
    match vs with
    | [] ->
       ...
    | v :: vs' ->
       ...(visit vs')...;;;
  

Example: unparsing polymorphic lists, revisited

In OCaml:

let show_list show_yourself vs =
  match vs with
  | [] ->
     "[]"
  | v :: vs' ->
     let rec show_list_aux v vs' =
       match vs' with
       | [] ->
          show_yourself v
       | v' :: vs'' ->
          (show_yourself v) ^ "; " ^ (show_list_aux v' vs'')
     in "[" ^ show_list_aux v vs' ^ "]";;

This OCaml function passes the unit tests:

# test_show_int_list (show_list show_int);;
- : bool = true
# test_show_bool_list (show_list show_bool);;
- : bool = true
# test_show_int_list_list (show_list (show_list show_int));;
- : bool = true
#

Example: computing the length of a list, revisited

In OCaml:

let list_length_v2 vs =
  let rec visit vs =
    match vs with
    | [] ->
       0
    | v :: vs' ->
       let ih = visit vs'
       in succ ih
  in visit vs;;

let list_length_v3 vs =
  let rec visit vs =
    match vs with
    | [] ->
       0
    | v :: vs' ->
       succ visit vs'
  in visit vs;;

These OCaml functions pass the unit test:

# test_list_length_int list_length_v2;;
- : bool = true
# test_list_length_int list_length_v3;;
- : bool = true
#

Example: computing the list of successive suffixes of a list

Let us implement a function that, given a list, yields the list of its successive suffixes, from this list all the way to the empty list:

let test_list_suffixes candidate =
  let b0 = (candidate [] = [[]])
  and b1 = (candidate [0] = [[0]; []])
  and b2 = (candidate [1; 0] = [[1; 0]; [0]; []])
  and b3 = (candidate [2; 1; 0] = [[2; 1; 0]; [1; 0]; [0]; []])
  (* etc. *)
  in b0 && b1 && b2 && b3;;

The suffixes function is defined following the inductive structure of lists:

• base case: the list of suffixes of the empty list is the singleton list containing this empty list
• induction step: given the list of suffixes vs's of a given list vs' (which is the induction hypothesis), the list of of suffixes of v :: vs' is (v :: vs') :: vs's

In OCaml:

let list_suffixes_v0 vs =
  let rec visit vs =
    match vs with
    | [] ->
       [[]]
    | v :: vs' ->
       let vs's = visit vs'
       in (v :: vs') :: vs's
  in visit vs;;

This implementation passes the unit test:

# test_list_suffixes list_suffixes_v0;;
- : bool = true
#

To simplify its definition, we can unfold the inner let expression since it is linear and vs's is immediately used:

In OCaml:

let list_suffixes_v1 vs =
  let rec visit vs =
    match vs with
    | [] ->
       [[]]
    | v :: vs' ->
       (v :: vs') :: (visit vs')
  in visit vs;;

This implementation passes the unit test:

# test_list_suffixes list_suffixes_v1;;
- : bool = true
#

Food for thought:

• in actuality, [[]] stands for [] :: []
• in the [] branch, [] :: [] could be written as vs :: []
• in the v :: vs' branch, (v :: vs') :: (visit vs') could be written as vs :: (visit vs')

In OCaml:

let list_suffixes_v2 vs =
  let rec visit vs =
    match vs with
    | [] ->
       vs :: []
    | v :: vs' ->
       vs :: (visit vs')
  in visit vs;;

This implementation passes the unit test:

# test_list_suffixes list_suffixes_v2;;
- : bool = true
#

Instead of cons’ing vs in each branch, we might as well do that prior to testing vs:

let list_suffixes_v3 vs =
  let rec visit vs =
    vs :: match vs with
          | [] ->
             []
          | v :: vs' ->
             visit vs'
  in visit vs;;

This implementation passes the unit test:

# test_list_suffixes list_suffixes_v3;;
- : bool = true
#

Note how visit proceeds in one pass, which leads to the suffixes being shared in the resulting list. For example, if the input list is [3; 2; 1], here is a depiction of the output:

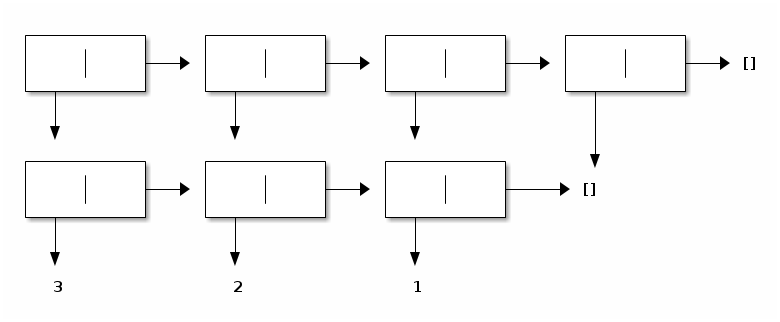
We can verify this sharing in the output using physical equality:

# let input_321 = [3; 2; 1];;
val input_321 : int list = [3; 2; 1]
# let output_321 = list_suffixes_v3 input_321;;
val output_321 : int list list = [[3; 2; 1]; [2; 1]; [1]; []]
# List.hd output_321 == input_321;;
- : bool = true
# List.hd (List.tl output_321) == List.tl input_321;;
- : bool = true
# List.hd (List.tl (List.tl output_321)) == List.tl (List.tl input_321);;
- : bool = true
# List.hd (List.tl (List.tl (List.tl output_321))) == List.tl (List.tl (List.tl input_321));;
- : bool = true
#

We can also verify that evaluating List.hd (List.tl output_321) == List.tl (List.hd output_321) yields true.

If the output list had no sharing, here is how it would be depicted:

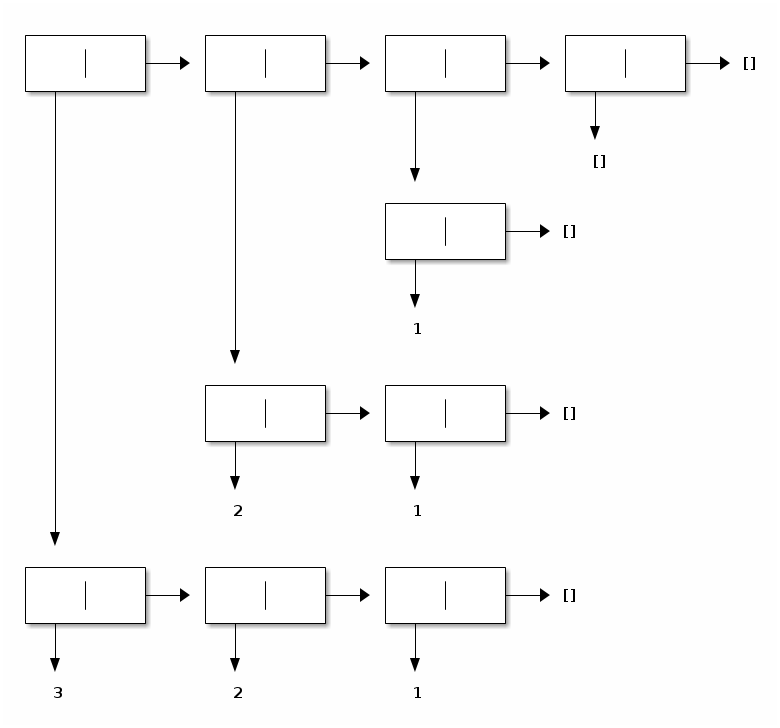
The size of this output list is proportional to the square of the size of the input list, and it could not be constructed in one pass over the input.

Exercise 1

Why is the size of the output list of successive suffixes without sharing proportional to the square of the size of the input list?

Postlude

Alfrothul: So the empty list is a polymorphic value.

Harald: That’s what OCaml says:

# [];;
- : 'a list = []
#

Alfrothul: Funny how we can use the empty list in the same expression at different types. Look:

# [] :: [];;
- : 'a list list = [[]]
#

3CPO: Cons’ing nil on nil? How perverse.

Halcyon: Well, ex nihilo nihil fit.

Harald: It’s a while since we haven’t constructed a proof tree, so how about we do that here to figure exactly what is going on. For some type variable t0, it root looks like:

. |- [] :: [] : t0

Alfrothul: There is no choice in the matter here, we can only use the CONS typing rule, where G is instantiated with ., e with [], es with [], and t with t1, for some type variable t1 such that t0 = t1 list:

     . |- [] : t1    . |- [] : t0
CONS ----------------------------
     . |- [] :: [] : t0

Harald: Let’s look at the left subtree. We can only use the NIL typing rule, where G is instantiated with . and t with t2, for some type variable t2 such that t1 = t2 list:

 NIL ------------
     . |- [] : t1    . |- [] : t0
CONS ----------------------------
     . |- [] :: [] : t0

Alfrothul: Ditto for the right subtree. We can also only use the NIL typing rule, where G is instantiated with . and t with t3, for some type variable t3 such that t0 = t3 list:

 NIL -------------    NIL ------------
     . |- [] : t1         . |- [] : t0
CONS ---------------------------------
     . |- [] :: [] : t0

Harald: And the proof tree is complete.

Alfrothul: We are left with the following typing constraints:

• t0 = t1 list
• t1 = t2 list
• t0 = t3 list

Harald: The first and the third equation imply a fourth:

• t3 = t1

Alfrothul: Replacing t1 by t2 list, we get:

• t0 = t2 list list

Harald: So we could construct the tree, and the constraints are not contradictory, i.e., the equations have are a solution with an unconstrained type variable t2, and so [] :: [], alias [[]], indeed has type 'a list list.

Alfrothul: What about [[[]]]?

Harald: Make a guess.

Alfrothul: No need:

# [[[]]];;
- : 'a list list list = [[[]]]
#

Harald: I think we have 3 instances of the empty list here:

# ([] :: []) :: [] = [[[]]];;
- : bool = true
#

Alfrothul: The empty list is indeed a polymorphic value.

Resources

• The OCaml code for the present lecture note (latest version: 16 Mar 2020).
• The resource file for Listy.cons and Listy.init (latest version: 16 Mar 2020).

Version

Added Exercise 0 as well as the postlude [17 Mar 2020]

Added the resource file for Listy.cons and Listy.init, at Koa Zhao Yuan’ implicit request [16 Mar 2020]

Only used match-expressions after having introduced them, thanks to Young Il Kim’s eagle eye [15 Mar 2020]

Fixed a typo in a use of list_suffixes_v3, thanks to Yoon Sangho’s eagle eye [15 Mar 2020]

Pointed out that the arguments of cons (i.e., :: in infix notation) are evaluated from right to left [14 Mar 2020]

Fixed a grammatical typo, thanks to Syed Muhammad Maaz’s eagle eye [14 Mar 2020]

Created [14 Mar 2020]