Polymorphic binary trees in OCaml¶
The goal of this lecture note is to study a particular concrete data type: polymorphic binary trees in OCaml.
Resources¶
- The OCaml code for the present lecture note (latest version: 02 Apr 2020).
Polymorphic binary trees¶
Here is how to declare the data type of binary trees where the payloads are stored in the leaves:
type 'a binary_tree =
| Leaf of 'a
| Node of 'a binary_tree * 'a binary_tree;;
Analyzing this definition,
- we declare a new data type (using the keyword type),
- this data type is named binary_tree,
- it is polymorphic (parameterized by 'a),
- it has two constructors (Leaf and Node),
- Leaf is unary (it take one argument), and
- Node is binary (it take two arguments: a left subtree and a right subtree).
Once this data type is declared, each of the expressions Leaf 1, Node (Leaf 1, Leaf 2), Node (Node (Leaf 1, Leaf 2), Leaf 3), and Node (Leaf 3, Node (Leaf 1, Leaf 2)) is syntactically correct, with type binary_tree:
# Leaf 1;;
- : int binary_tree = Leaf 1
# Node (Leaf 1, Leaf 2);;
- : int binary_tree = Node (Leaf 1, Leaf 2)
# Node (Node (Leaf 1, Leaf 2), Leaf 3);;
- : int binary_tree = Node (Node (Leaf 1, Leaf 2), Leaf 3)
# Node (Leaf 1, Node (Leaf 2, Leaf 3));;
- : int binary_tree = Node (Leaf 1, Node (Leaf 2, Leaf 3))
#
A sample of binary trees¶
Here is how to construct 5 binary trees of integers:
one containing just one leaf:
let t0 = Leaf 0;;
pictorially:

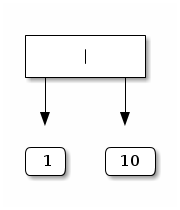
one containing one node and two leaves:
let t1 = Node (Leaf 1, Leaf 10);;
pictorially:
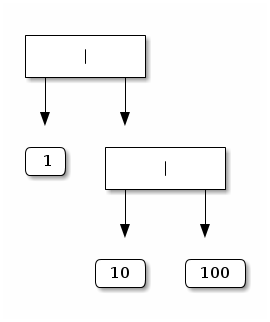
one containing two nodes and three leaves:
let t2 = Node (Leaf 1, Node (Leaf 10, Leaf 100));;
pictorially:
another one containing two nodes and three leaves:
let t3 = Node (Node (Leaf 1, Leaf ~-10), Leaf 100);;
pictorially:

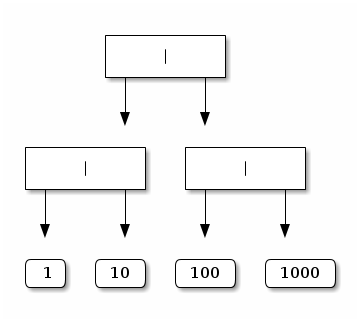
one containing three node and four leaves:
let t4 = Node (Node (Leaf 1, Leaf 10), Node (Leaf 100, Leaf 1000));;
pictorially:
On the occasion, it is a good idea to systematically indent the constructors in these declarations, so that their semantic tree structure (what these definitions mean) is reflected syntactically (how they are written):
let t4 = Node (Node (Leaf 1,
Leaf 10),
Node (Leaf 100,
Leaf 1000));;
This layout makes it clear that
the tree denoted by t4 has 4 leaves that contain the integers 1, 10, 100, and 1000,
it has 3 nodes,
the least integer contained in its leaves is 1, in the left subtree of its left subtree,
the largest integer contained in its leaves is 1000, in the right subtree of its right subtree,
its weight is 1111 (i.e., the sum of the integers in its leaves: 1 + 10 + 100 + 1000),
its height is 2 (and the height of the tree denoted by t0 is 0), and
since
- at depth 0, it has 1 node,
- at depth 1, it has 2 nodes,
- at depth 2, it has 4 leaves,
its width is 4.
Unparsing binary trees¶
To unparse any given binary tree into a string (such that the content of this string is an OCaml expression such that evaluating this expression yields the given binary tree), we need to traverse it recursively:
let test_show_binary_tree_int candidate =
(* test_show_binary_tree : (binary_tree -> string) -> bool *)
let b0 = (candidate
(Leaf 0)
= "Leaf 0")
and b1 = (candidate
(Node (Leaf 1, Leaf 10))
= "Node (Leaf 1, Leaf 10)")
and b2 = (candidate
(Node (Leaf 1, Node (Leaf 10, Leaf 100)))
= "Node (Leaf 1, Node (Leaf 10, Leaf 100))")
and b3 = (candidate
(Node (Node (Leaf 1, Leaf 10), Leaf 100))
= "Node (Node (Leaf 1, Leaf 10), Leaf 100)")
and b4 = (candidate
(Node (Node (Leaf 1, Leaf 10), Node (Leaf 100, Leaf 1000)))
= "Node (Node (Leaf 1, Leaf 10), Node (Leaf 100, Leaf 1000))")
(* etc. *)
in b0 && b1 && b2 && b3 && b4;;
Formally, the function is specified inductively, following the structure of binary trees:
base case:
for any integer n (noting its syntactic representation as n), unparsing Leaf n is achieved by concatenating the string "Leaf " and the unparsed counterpart of n
induction step:
for any binary tree t1 (resp. t2) whose unparsed counterpart is s1, which is the left induction hypothesis (resp. s2, which is the right induction hypothesis), the unparsed counterpart of Node (t1, t2) is obtained by concatenating "Node (", s1, ", ", s2, and ")"
In OCaml, this function is implemented as a structurally recursive function mapping a binary tree to a string:
let show_binary_tree show_yourself t =
(* show_binary_tree : ('a -> string) -> 'a binary_tree -> string *)
let rec visit t =
match t with
| Leaf v ->
"Leaf " ^ (show_yourself v)
| Node (t1, t2) ->
"Node (" ^ visit t1 ^ ", " ^ visit t2 ^ ")"
in visit t;;
Indeed,
- visit is recursive because it calls itself, and
- it is structurally recursive because it follows the structure of the inductive data type of binary trees; in particular, its recursive call over the left subtree t1 implements the left induction hypothesis, and its recursive call over the right subtree t2 implements the right induction hypothesis.
This OCaml function passes the unit tests:
# test_show_binary_tree_int (show_binary_tree show_int);;
- : bool = true
#
Should we want to name the result of the recursive calls, we would need to do it consistently with the order in which OCaml evaluates subexpressions (i.e., right to left) so that the corresponding compound let-expression is cosmetic:
let show_binary_tree' show_yourself t =
(* show_binary_tree : ('a -> string) -> 'a binary_tree -> string *)
let rec visit t =
match t with
| Leaf v ->
"Leaf " ^ (show_yourself v)
| Node (t1, t2) ->
let s2 = visit t2
and s1 = visit t1
in "Node (" ^ s1 ^ ", " ^ s2 ^ ")"
in visit t;;
In addition, the resource file accompanying the present lecture note contains a pretty-printing function of type ('a -> string) -> 'a binary_tree -> unit that renders a given binary tree in an indented fashion:
# pretty_print_binary_tree show_int (Node (Leaf 1, Node (Leaf 10, Leaf 100)));;
Node (Leaf 1,
Node (Leaf 10,
Leaf 100))
- : unit = ()
# pretty_print_binary_tree show_bool (Node (Leaf true, Node (Leaf false, Leaf false)));;
Node (Leaf true,
Node (Leaf false,
Leaf false))
- : unit = ()
#
Number of leaves¶
How many leaves are there in a given binary tree?
Intuitively, the unit-test function is simple to write – for any given binary tree, the candidate function should return the number obtained by counting all the leaves in this tree, i.e., by counting the number of occurrences of the Leaf constructor in this tree:
let test_number_of_leaves_int candidate =
(* test_number_of_leaves_int : (binary_tree -> int) -> bool *)
let b0 = (candidate (Leaf 0)
= 1)
and b1 = (candidate (Node (Leaf 1,
Leaf 10))
= 2)
and b2 = (candidate (Node (Leaf 1,
Node (Leaf 10,
Leaf 100)))
= 3)
and b3 = (candidate (Node (Node (Leaf 1,
Leaf 10),
Leaf 100))
= 3)
and b4 = (candidate (Node (Node (Leaf 1,
Leaf 10),
Node (Leaf 100,
Leaf 1000)))
= 4)
(* etc. *)
in b0 && b1 && b2 && b3 && b4;;
Formally, the function is specified inductively, following the structure of binary trees:
base case:
for any integer n (noting its syntactic representation as n), the number of leaves in Leaf n is 1
induction step:
for any binary tree t1 (resp. t2) whose number of leaves is l1, which is the left induction hypothesis (resp. l2, which is the right induction hypothesis), the number of leaves in Node (t1, t2) is the sum of l1 and l2 to account for the leaves in t1 and in t2
In OCaml, this function is implemented as a structurally recursive function mapping a binary tree to a positive integer:
let number_of_leaves_v0 t =
(* number_of_leaves_v0 : 'a binary_tree -> int *)
let rec visit t =
match t with
| Leaf v ->
1
| Node (t1, t2) ->
let l2 = visit t2
and l1 = visit t1
in l1 + l2
in visit t;;
Again,
- visit is recursive because it calls itself (and is declared with the keyword rec), and
- it is structurally recursive because it follows the structure of the inductive data type of binary trees; in particular, each of the recursive calls implements an induction hypothesis.
This OCaml function passes the unit tests:
# test_number_of_leaves_int number_of_leaves_v0;;
- : bool = true
#
In the induction step, the compound let expression naming the result of the two recursive calls to visit is cosmetic, so we can unfold it and replace each name (i.e., l2 and l1) with the corresponding definiens (i.e., visit t2 and visit t1) in the body of the let expression (i.e., l1 + l2):
let number_of_leaves_v1 t =
(* number_of_leaves_v1 : 'a binary_tree -> int *)
let rec visit t =
match t with
| Leaf v ->
1
| Node (t1, t2) ->
visit t1 + visit t2
in visit t;;
This OCaml function also passes the unit test:
# test_number_of_leaves_int number_of_leaves_v1;;
- : bool = true
#
To visualize the calls and returns that take place when computing the number of leaves in any given tree, the resource file accompanying the present lecture note contains two traced versions:
# traced_number_of_leaves show_int (Node (Leaf 1, Node (Leaf 10, Leaf 100)));;
number_of_leaves (Node (Leaf 1, Node (Leaf 10, Leaf 100))) ->
visit (Node (Leaf 1, Node (Leaf 10, Leaf 100))) ->
visit (Node (Leaf 10, Leaf 100)) ->
visit (Leaf 100) ->
visit (Leaf 100) <- 1
visit (Leaf 10) ->
visit (Leaf 10) <- 1
visit (Node (Leaf 10, Leaf 100)) <- 2
visit (Leaf 1) ->
visit (Leaf 1) <- 1
visit (Node (Leaf 1, Node (Leaf 10, Leaf 100))) <- 3
number_of_leaves (Node (Leaf 1, Node (Leaf 10, Leaf 100))) <- 3
- : int = 3
# prettily_traced_number_of_leaves show_int (Node (Leaf 1, Node (Leaf 10, Leaf 100)));;
number_of_leaves (Node (Leaf 1,
Node (Leaf 10,
Leaf 100))) ->
visit (Node (Leaf 1,
Node (Leaf 10,
Leaf 100))) ->
visit (Node (Leaf 10,
Leaf 100)) ->
visit (Leaf 100) ->
visit (Leaf 100) <- 1
visit (Leaf 10) ->
visit (Leaf 10) <- 1
visit (Node (Leaf 10,
Leaf 100)) <- 2
visit (Leaf 1) ->
visit (Leaf 1) <- 1
visit (Node (Leaf 1,
Node (Leaf 10,
Leaf 100))) <- 3
number_of_leaves (Node (Leaf 1,
Node (Leaf 10,
Leaf 100))) <- 3
- : int = 3
#
Observe how the trace respects OCaml’s left-to-right order of evaluation for subexpressions.
Number of nodes¶
How many nodes are there in a given binary tree?
Intuitively, the unit-test function is simple to write – for any given binary tree, the candidate function should return the number obtained by counting all the nodes in this tree, i.e., by counting the number of occurrences of the Node constructor in this tree:
let test_number_of_nodes_int candidate =
(* test_number_of_nodes_int : (binary_tree -> int) -> bool *)
let b0 = (candidate (Leaf 0)
= 0)
and b1 = (candidate (Node (Leaf 1,
Leaf 10))
= 1)
and b2 = (candidate (Node (Leaf 1,
Node (Leaf 10,
Leaf 100)))
= 2)
and b3 = (candidate (Node (Node (Leaf 1,
Leaf 10),
Leaf 100))
= 2)
and b4 = (candidate (Node (Node (Leaf 1,
Leaf 10),
Node (Leaf 100,
Leaf 1000)))
= 3)
(* etc. *)
in b0 && b1 && b2 && b3 && b4;;
Formally, the property is expressed inductively, following the structure of binary trees:
base case:
for any integer n (noting its syntactic representation as n), the number of nodes in Leaf n is 0
induction step:
for any binary tree t1 (resp. t2) whose number of nodes is n1, which is the left induction hypothesis (resp. n2, which is the right induction hypothesis), the number of nodes of Node (t1, t2) is the sum of n1 and n2 to account for the nodes in t1 and t2, plus 1 to account for the node that holds t1 and t2 together
In OCaml, this function is implemented as a structurally recursive function mapping a binary tree to a non-negative integer:
let number_of_nodes_v0 t =
(* number_of_nodes_v0 : binary_tree -> int *)
let rec visit t =
match t with
| Leaf v ->
0
| Node (t1, t2) ->
let n2 = visit t2
and n1 = visit t1
in succ (n1 + n2)
in visit t;;
Again,
- visit is recursive because it calls itself (and is declared with the keyword rec), and
- it is structurally recursive because it follows the structure of the inductive data type of binary trees; in particular, each of the recursive calls implements an induction hypothesis.
This OCaml function passes the unit test:
# test_number_of_nodes_int number_of_nodes_v0;;
- : bool = true
#
Again, in the induction step, the compound let expression naming the result of the two recursive calls to visit is cosmetic, so we can unfold it and replace each name (i.e., n2 and n1) with the corresponding definiens (i.e., visit t2 and visit t1) in the body of the let expression (i.e., succ (n1 + n2)):
let number_of_nodes_v1 t =
(* number_of_nodes_v1 : binary_tree -> int *)
let rec visit t =
match t with
| Leaf v ->
0
| Node (t1, t2) ->
succ (visit t1 + visit t2)
in visit t;;
This OCaml function also passes the unit test:
# test_number_of_nodes_int number_of_nodes_v1;;
- : bool = true
#
Interlude¶
Alfrothul: Did you see that test_number_of_leaves and test_number_of_nodes use the same trees?
Harald: I didn’t particularly notice, but why not? This way, they are easier to compare. Also, gratuitous variations are rarely a good idea when writing programs.
Alfrothul: Did you compare the expected results, in each test?
Harald: Oh. They are comparable indeed.
Alfrothul: Do you think that this comparison holds true for any tree?
Harald: I guess that would be something to prove by structural induction...
Alfrothul: It doesn’t even look too hard.
Harald: So... The property we want to prove is that for any tree, its number of leaves is its number of nodes, plus 1.
Alfrothul: Dibs on the base case! A leaf contains one leaf and zero nodes.
Harald: Right – indeed for any integer n (noting its syntactic representation as n), evaluating number_of_leaves (Leaf n) yields 1, evaluating number_of_nodes (Leaf n) yields 0, and 1 = 0 + 1.
Alfrothul: Now for the induction step... We are given two trees t1 and t2 such as
- t1 contains l1 leaves and n1 nodes, and l1 = n1 + 1, and
- t2 contains l2 leaves and n2 nodes, and l2 = n2 + 1.
Harald: Let’s look at the tree consisting of a node whose left subtree is t1 and whose right subtree is t2.
Alfrothul: This tree has l1 + l2 leaves.
Harald: And it has n1 + n2 + 1 nodes.
Alfrothul: Since l1 = n1 + 1...
Harald (helpfully interjecting a precision): Which is the first induction hypothesis.
Alfrothul (continuing): ...and l2 = n2 + 1,
Harald (interjecting another precision): Which is the second induction hypothesis.
Alfrothul: ... l1 + l2 = n1 + 1 + n2 + 1. And thanks.
Harald: So the number of leaves of this tree, i.e., l1 + l2, is indeed its number of nodes, i.e., n1 + n2 + 1, plus 1.
Alfrothul: So this comparison holds true for any tree.
Harald: Even when the tree is, like, imbalanced?
Alfrothul: That’s what the maths say. The grammar for binary trees is not just sound (all OCaml values obtained using the constructors Leaf and Node represent binary trees), it is also complete (all binary trees can be constructed using Leaf and Node). So if it is a binary tree, its number of leaves is its number of nodes, plus 1, no matter its shape.
Exercise 26¶
Specify and implement a function that computes the least integer contained in a given binary tree of integers.
Exercise 27¶
Specify and implement a function that computes the largest integer contained in a given binary tree of integers.
Exercise 28¶
Specify and implement a function that computes the weight of a given binary tree of integers, i.e., the sum of the integers in its leaves.
Height¶
The height of a binary tree is the number of layers it takes to draw it, starting at 0:
A binary tree of height 0:

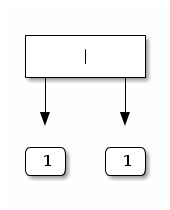
A (symmetric) binary tree of height 1:
A (left-balanced) binary tree of height 2:
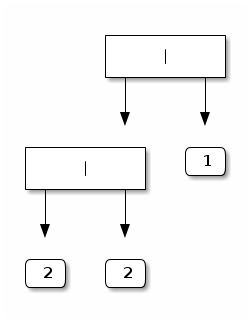
A (right-balanced) binary tree of height 3:
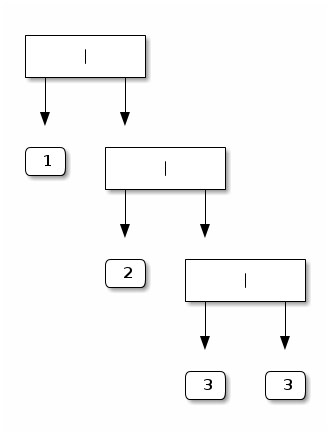
Again, the unit-test function pretty much writes itself:
let test_height_int candidate =
(* test_height_int: (binary_tree -> int) -> bool *)
let b0 = (candidate (Leaf 0)
= 0)
and b1 = (candidate (Node (Leaf 10,
Leaf 11))
= 1)
and b2 = (candidate (Node (Leaf 10,
Node (Leaf 20,
Leaf 21)))
= 2)
and b3 = (candidate (Node (Leaf 10,
Node (Leaf 20,
Node (Leaf 30,
Leaf 31))))
= 3)
and b4 = (candidate (Node (Node (Leaf 20,
Leaf 21),
Node (Leaf 22,
Node (Leaf 30,
Leaf 31))))
= 3)
and b5 = (candidate (Node (Node (Node (Leaf 30,
Leaf 31),
Leaf 20),
Node (Leaf 21,
Node (Leaf 32,
Leaf 33))))
= 3)
and b6 = (candidate (Node (Node (Node (Leaf 30,
Node (Leaf 40,
Leaf 41)),
Leaf 20),
Node (Leaf 21,
Node (Leaf 31,
Leaf 21))))
= 4)
and b7 = (candidate (Node (Leaf 10,
Node (Leaf 20,
Node (Leaf 30,
Node (Leaf 40,
Node (Leaf 50,
Node (Leaf 60,
Node (Leaf 70,
Leaf 71))))))))
= 7)
and b8 = (candidate (Node (Node (Node (Node (Node (Node (Node (Node (Leaf 80,
Leaf 81),
Leaf 70),
Leaf 60),
Leaf 50),
Leaf 40),
Leaf 30),
Leaf 20),
Leaf 10))
= 8)
(* etc. *)
in b0 && b1 && b2 && b3 && b4 && b5 && b6 && b7 && b8;;
Formally, the height function is specified inductively, following the structure of binary trees:
base case:
given any integer n, the height of Leaf n is 0
induction step:
given any tree t1 of height h1 (which is the left induction hypothesis) and given any tree t2 of height h2 (which is the right induction hypothesis), the height of Node (t1, t2) is the maximum of h1 and h2, plus 1
In OCaml, the height function is implemented as a structurally recursive function that follows the inductive specification just above and maps a binary tree to an integer:
let height_v0 t =
(* height_v0 : 'a binary_tree -> int *)
let rec visit t =
match t with
| Leaf n ->
0
| Node (t1, t2) ->
let h2 = visit t2
and h1 = visit t1
in succ (max h1 h2)
in visit t;;
Analysis:
- visit is recursive because it calls itself (and is declared with the keyword rec), and
- it is structurally recursive because it follows the structure of the inductive data type of binary trees; in particular, each of the recursive calls implements an induction hypothesis.
This OCaml function passes the unit tests:
# test_height_int height_v0;;
- : bool = true
#
In the accompanying .ml file, this unit test is automated as an assertion.
One more time, in the induction step, the compound let expression naming the result of the two recursive calls to visit is cosmetic, so it can be unfolded and each name (i.e., h1 and h2) can be replaced with the corresponding definiens (i.e., visit t1 and visit t2) in the body of the let expression (i.e., succ (h1 + h2)).
Mirror¶
How do we implement a function that mirrors any given binary tree?
Intuitively, the unit-test function is simple to write – for any given binary tree, the candidate function should return the mirror image of this tree:
let test_mirror_int candidate =
(* test_mirror_int : (int binary_tree -> int binary_tree) -> bool *)
let b0 = (candidate
(Leaf 10)
= (Leaf 10))
and b1 = (candidate
(Node (Leaf 10,
Leaf 20))
= (Node (Leaf 20,
Leaf 10)))
and b2 = (candidate
(Node (Leaf 10,
Node (Leaf 20,
Leaf 30)))
= (Node (Node (Leaf 30,
Leaf 20),
Leaf 10)))
and b3 = (candidate
(Node (Node (Leaf 10,
Leaf 20),
Node (Leaf 30,
Leaf 40)))
= (Node (Node (Leaf 40,
Leaf 30),
Node (Leaf 20,
Leaf 10))))
(* etc.*)
in b0 && b1 && b2 && b3;;
Formally, the mirror function is specified inductively, following the structure of binary trees:
base case:
given a value v, the mirror image of Leaf v is Leaf v
induction step:
given a binary tree t1 whose mirror image is ih1 (which is the left induction hypothesis) and given a binary tree t2 whose mirror image is ih2 (which is the right induction hypothesis), the mirror image of Node (t1, t2) is Node (ih2, ih1)
In OCaml, the mirroring function is implemented as a structurally recursive function that follows the inductive specification just above and maps a binary tree to another one:
let mirror_v0 t =
(* mirror_v0 : 'a binary_tree -> 'a binary_tree *)
let rec visit t =
match t with
| Leaf v ->
Leaf v
| Node (t1, t2) ->
let ih2 = visit t2
and ih1 = visit t1
in Node (ih2, ih1)
in visit t;;
Analysis:
- visit is recursive because it calls itself (and is declared with the keyword rec), and
- it is structurally recursive because it follows the structure of the inductive data type of binary trees; in particular, each of the recursive calls implements an induction hypothesis.
This OCaml function passes the unit tests:
# test_mirror_int mirror_v0;;
- : bool = true
#
A mirror in a mirror¶
Mirroring a mirrored tree should give back the original tree, prior to the first mirroring. In mathematical terms, the mirror function is involutory, i.e., an involution.
Let us prove that property by structural induction over trees.
Proposition: for all t, visit (visit t) = t, where visit is the local recursive function in the definition of mirror_v0.
Proof: by structural induction on t
base case:
given a value v, we need to show that visit (visit (Leaf v)) = Leaf v:
visit (visit (Leaf v)) = { by definition of visit in the base case } visit (Leaf v) = { by definition of visit in the base case } Leaf vwhich is what we needed to show
induction step:
given a tree t1 such that visit (visit t1) = t1 (which is the left induction hypothesis) and given a tree t2 such that visit (visit t2) = t2 (which is the right induction hypothesis), we need to show that visit (visit (Node (t1, t2))) = Node (t1, t2):
visit (visit (Node (t1, t2))) = { by definition of visit in the induction step } visit (Node (visit t2, visit t1)) = { by definition of visit in the induction step } Node (visit (visit t1), visit (visit t2)) = { by the first induction hypothesis } Node (t1, visit (visit t2)) = { by the second induction hypothesis } Node (t1, t2)which is what we needed to show
So the proposition holds for all possible binary trees, and we can extend the definition of the unit-test function with this property:
let test_mirror_int candidate =
(* test_mirror_int : (int binary_tree -> int binary_tree) -> bool *)
...
and b4 = (let t = (Node (Node (Leaf 10,
Leaf 20),
Node (Leaf 30,
Node (Leaf 40,
Leaf 50))))
in candidate (candidate t) = t)
(* etc. *)
in b0 && b1 && b2 && b3 && b4;;
Generating random binary trees of integers¶
Let us write an OCaml function generating a random tree of at most a given height. We cannot write a unit-test function for it, since its output will be random, so the only thing we can warrant is its type, in that it should map a given non-negative integer to a binary tree of integers.
Let us specify this function by induction over an upper bound of the height of the resulting tree:
base case (the height is 0)
a tree of height 0 is a leaf
induction step (the height is n’ + 1, for some n’)
given two trees t1 and t2 of height at most n’, the resulting tree is either a leaf or a node with t1 and t2 as its left subtree and right subtree
In OCaml:
let generate_random_binary_tree_int n =
let () = assert (n >= 0) in
let rec visit n =
if n = 0
then Leaf (Random.int 10)
else match Random.int 3 with
| 0 ->
Leaf (pred (- (Random.int 5)))
| _ ->
let n' = pred n
in Node (visit n', visit n')
in visit n;;
Analysis:
- generate_random_binary_tree_int expects a non-negative integer
- in the base case, it returns a leaf containing a random integer between 0 and 9
- in the induction step,
- in one case out of three, it returns a leaf containing a random integer between -5 and -1
- in two cases out of three, and given two random trees, one of height at most h1 - 1, and the other of height at most h2 - 1, it returns a node containing these two trees, and whose height is the largest of h1 and h2
To wit:
# pretty_print_binary_tree show_int (generate_random_binary_tree_int 5);;
Leaf ~-1
- : unit = ()
# pretty_print_binary_tree show_int (generate_random_binary_tree_int 5);;
Node (Leaf 0,
Node (Node (Leaf ~-6,
Node (Leaf 0,
Node (Leaf 8,
Leaf 4))),
Node (Leaf ~-8,
Leaf ~-4)))
- : unit = ()
# pretty_print_binary_tree show_int (generate_random_binary_tree_int 5);;
Leaf ~-6
- : unit = ()
# pretty_print_binary_tree show_int (generate_random_binary_tree_int 5);;
Node (Leaf ~-5,
Node (Node (Leaf ~-4,
Node (Node (Leaf 0,
Leaf 2),
Leaf ~-1)),
Node (Node (Node (Leaf 0,
Leaf 4),
Node (Leaf 5,
Leaf 4)),
Node (Node (Leaf 3,
Leaf 8),
Node (Leaf 6,
Leaf 7)))))
- : unit = ()
#
The resource file accompanying the present lecture note also contains a polymorphic generator of random binary trees of type (int -> 'a) -> int -> 'a binary_tree:
# pretty_print_binary_tree show_string (generate_random_binary_tree string_of_int 5);;
Node (Node (Leaf "-1",
Leaf "-3"),
Node (Node (Node (Node (Leaf "7",
Leaf "0"),
Node (Leaf "2",
Leaf "4")),
Node (Node (Leaf "4",
Leaf "1"),
Leaf "-5")),
Node (Node (Node (Leaf "1",
Leaf "7"),
Node (Leaf "7",
Leaf "0")),
Node (Node (Leaf "2",
Leaf "2"),
Node (Leaf "9",
Leaf "7")))))
- : unit = ()
# pretty_print_binary_tree show_bool (generate_random_binary_tree (fun n -> n mod 2 = 0) 5);;
Node (Node (Node (Node (Leaf true,
Node (Leaf false,
Leaf true)),
Node (Leaf false,
Leaf true)),
Node (Node (Node (Leaf false,
Leaf true),
Leaf true),
Leaf true)),
Leaf true)
- : unit = ()
#
Analysis:
- in the first interaction, a random binary tree of strings is generated and then rendered, and
- in the second interaction, a random binary tree of Booleans is generated and then rendered.
The mirror function, revisited¶
We are now in position to flesh out the unit-test function with random binary trees:
let test_mirror_int candidate =
(* test_mirror_int : (int binary_tree -> int binary_tree) -> bool *)
let b0 = (candidate
(Leaf 10)
= (Leaf 10))
...
and b5 = (let t = generate_random_binary_tree_int 10
in if candidate (candidate t) = t
then true
else let () = Printf.printf "The mirror-mirror test failed on %s\n" (show_binary_tree show_int t) in
false)
(* etc. *)
in b0 && b1 && b2 && b3 && b4 && b5;;
Interlude¶
Alfrothul: Did you see how the test_mirror_int now prints out the random tree that failed the test?
Harald: Well, it would be pretty useless to be told that a random test failed without being told about the failure point.
Alfrothul: Frustrating, even. Let’s test this test function, shall we?
Harald: Good idea. We need an erroneous mirror function.
Alfrothul: How about the identity function:
# test_mirror_int (fun t -> t);;
- : bool = false
#
Alfrothul: Yay, false.
Harald: But where is the error message?
Alfrothul: Oops. Where is the error message?
Brynja: Nowhere, since the identity function is also involutory.
Alfrothul: Ahem.
Harald: Er... How about we compose the mirror function an odd number of times? No, wait, that won’t work, because composing it with itself yields it being applied an even number of times.
Alfrothul: And since it is involutory...
Harald: How about we program a distorted mirror function?
Alfrothul: A distorted mirror function.
Harald: Well, yes, one that randomly negates the integers in the leaves:
let distorted_mirror_int t =
(* distorted_mirror_int : int binary_tree -> int binary_tree *)
let rec visit t =
match t with
| Leaf n ->
Leaf (if Random.bool ()
then n
else -n)
| Node (t1, t2) ->
let ih2 = visit t2
and ih1 = visit t1
in Node (ih2, ih1)
in visit t;;
Alfrothul: Right, that ought to do it:
# test_mirror_int distorted_mirror_int;;
The mirror-mirror test failed on Leaf ~-2
- : bool = false
#
Harald: And indeed it does.
Alfrothul: That’s a big hammer. How about a constant function:
# test_mirror_int (fun t -> Leaf 42);;
The mirror-mirror test failed on Node (Leaf ~-1, Node (Node (Node (Leaf ~-5, Node (Node (Node (Node (Leaf ~-3, Node (Leaf ~-5, Leaf ~-5)), Node (Leaf ~-1, Leaf ~-4)), Node (Node (Node (Node (Leaf 6, Leaf 7), Leaf ~-5), Node (Node (Leaf 5, Leaf 0), Node (Leaf 4, Leaf 1))), Node (Node (Node (Leaf 9, Leaf 5), Node (Leaf 1, Leaf 8)), Node (Node (Leaf 0, Leaf 4), Leaf ~-5)))), Leaf ~-5)), Node (Node (Node (Leaf ~-3, Leaf ~-5), Node (Node (Node (Node (Node (Leaf 9, Leaf 3), Node (Leaf 1, Leaf 8)), Leaf ~-5), Node (Leaf ~-5, Leaf ~-4)), Node (Node (Leaf ~-3, Leaf ~-5), Node (Node (Node (Leaf 6, Leaf 6), Node (Leaf 8, Leaf 8)), Node (Node (Leaf 8, Leaf 9), Node (Leaf 8, Leaf 3)))))), Node (Node (Node (Leaf ~-4, Node (Node (Node (Leaf 6, Leaf 0), Node (Leaf 6, Leaf 4)), Node (Node (Leaf 9, Leaf 9), Node (Leaf 3, Leaf 1)))), Node (Node (Node (Leaf ~-5, Node (Leaf 6, Leaf 9)), Node (Leaf ~-2, Leaf ~-4)), Node (Node (Node (Leaf 2, Leaf 6), Leaf ~-3), Leaf ~-3))), Leaf ~-2))), Node (Node (Node (Leaf ~-5, Node (Node (Node (Node (Leaf ~-4, Node (Leaf 5, Leaf 8)), Leaf ~-1), Node (Node (Node (Leaf 8, Leaf 6), Node (Leaf 3, Leaf 8)), Node (Node (Leaf 9, Leaf 8), Node (Leaf 1, Leaf 7)))), Leaf ~-3)), Node (Leaf ~-1, Node (Node (Node (Node (Node (Leaf 5, Leaf 0), Node (Leaf 1, Leaf 1)), Node (Node (Leaf 5, Leaf 3), Node (Leaf 4, Leaf 2))), Node (Node (Node (Leaf 4, Leaf 7), Node (Leaf 1, Leaf 3)), Leaf ~-5)), Leaf ~-5))), Leaf ~-1)))
- : bool = false
#
Harald: And you call that a smaller hammer?
Alfrothul: The hammer is smaller, but the result of smashing the unit-test function with it is just as big as with your distorted mirror:
# test_mirror_int distorted_mirror_int;;
The mirror-mirror test failed on Node (Node (Node (Node (Leaf ~-3, Node (Leaf ~-2, Node (Node (Node (Leaf ~-1, Node (Leaf ~-3, Node (Leaf 6, Leaf 9))), Node (Leaf ~-2, Node (Leaf ~-5, Node (Leaf 8, Leaf 3)))), Node (Leaf ~-4, Node (Node (Node (Leaf 3, Leaf 9), Leaf ~-4), Node (Node (Leaf 1, Leaf 7), Node (Leaf 5, Leaf 4))))))), Node (Node (Node (Leaf ~-4, Leaf ~-5), Leaf ~-3), Node (Node (Leaf ~-2, Node (Node (Node (Node (Leaf 3, Leaf 6), Leaf ~-1), Node (Node (Leaf 6, Leaf 6), Node (Leaf 1, Leaf 7))), Leaf ~-5)), Node (Node (Node (Node (Node (Leaf 1, Leaf 7), Node (Leaf 9, Leaf 8)), Leaf ~-2), Leaf ~-3), Node (Node (Node (Leaf ~-5, Leaf ~-2), Node (Node (Leaf 3, Leaf 7), Leaf ~-5)), Node (Node (Node (Leaf 7, Leaf 9), Node (Leaf 4, Leaf 9)), Node (Leaf ~-1, Leaf ~-2))))))), Node (Node (Leaf ~-3, Node (Leaf ~-5, Node (Node (Node (Node (Node (Leaf 4, Leaf 3), Leaf ~-4), Node (Node (Leaf 0, Leaf 3), Node (Leaf 9, Leaf 9))), Node (Leaf ~-1, Node (Node (Leaf 2, Leaf 4), Leaf ~-5))), Node (Node (Node (Node (Leaf 5, Leaf 8), Node (Leaf 1, Leaf 8)), Node (Node (Leaf 9, Leaf 8), Node (Leaf 3, Leaf 0))), Leaf ~-3)))), Leaf ~-4)), Node (Leaf ~-5, Node (Node (Leaf ~-4, Node (Node (Node (Leaf ~-3, Node (Node (Node (Leaf 6, Leaf 8), Node (Leaf 5, Leaf 3)), Node (Node (Leaf 1, Leaf 5), Node (Leaf 2, Leaf 7)))), Node (Node (Leaf ~-2, Node (Leaf ~-4, Node (Leaf 6, Leaf 7))), Leaf ~-2)), Node (Node (Leaf ~-4, Node (Leaf ~-4, Leaf ~-3)), Leaf ~-1))), Node (Node (Leaf ~-1, Node (Leaf ~-4, Leaf ~-3)), Leaf ~-1))))
- : bool = false
#
Harald: I was just saying. Still, your smaller hammer may fail to make the unit test fail, in case Leaf 42 is one of the tested trees.
Alfrothul: That can’t be, since it isn’t one of the trees (I checked), and the random generator can’t generate it, since it only generates leaves between 0 and 9 and between -5 and -1 (I also checked).
Harald: Shall we move on?
Calder mobiles¶
A mobile is a kinetic sculpture that can be represented as a binary tree: the nodes are the (weightless) bars, and the leaves are the weighted objects.
A binary tree of integers represents a well-balanced mobile whenever for each node, the weight of the left subtree is the same as the weight of the right subtree:
let test_well_balanced candidate =
let b0 = (candidate (Leaf 1)
= true)
and b1 = (candidate (Node (Leaf 1,
Leaf 1))
= true)
and b2 = (candidate (Node (Leaf 1,
Leaf 2))
= false)
and b3 = (candidate (Node (Leaf 2,
Leaf 1))
= false)
and b4 = (candidate (Node (Node (Leaf 1,
Leaf 1),
Leaf 2))
= true)
and b5 = (candidate (Node (Leaf 2,
Node (Leaf 1,
Leaf 1)))
= true)
and b6 = (candidate (Node (Node (Leaf 2,
Node (Leaf 1,
Leaf 1)),
Node (Node (Node (Leaf 1,
Leaf 1),
Node (Leaf 1,
Leaf 1)),
Leaf 4)))
= false)
and b7 = (candidate (Node (Node (Leaf 2,
Node (Leaf 1,
Leaf 1)),
Node (Node (Node (Leaf 1,
Leaf 1),
Node (Leaf 1,
Leaf 1)),
Leaf 6)))
= false)
and b8 = (candidate (Node (Node (Leaf 4,
Node (Leaf 2,
Leaf 2)),
Node (Node (Node (Leaf 2,
Leaf 1),
Node (Leaf 1,
Leaf 2)),
Leaf 6)))
= false)
(* etc. *)
in b0 && b1 && b2 && b3 && b4 && b5 && b6 && b7 && b8;;
Exercise 29¶
Specify and implement a function that tests whether a given binary tree of integers represents a well-balanced mobile. How many recursive calls are involved to carry out this test?
Hint: a solution exists that operates in one pass over the input tree.
The map function over polymorphic binary trees¶
Like String.map in Week 05 and like map_list (and List.map) in Week 09, a polymorphic map function exists for binary trees. Given a function and a binary tree, this map function applies this function to each of the payloads of this binary tree and collects the results in a new tree which is isomorphic to (i.e., has the same structure as) the given tree:
let test_map_binary_tree_int candidate =
let b0 = (candidate succ
(Leaf 0)
= Leaf 1)
and b1 = (candidate pred
(Leaf 0)
= Leaf ~-1)
and b2 = (candidate succ
(Node (Leaf 0,
Leaf 1))
= Node (Leaf 1,
Leaf 2))
and b3 = (candidate pred
(Node (Leaf 0,
Leaf 1))
= Node (Leaf ~-1,
Leaf 0))
and b4 = (candidate (fun n -> n * n)
(Node (Node (Leaf 1,
Leaf 2),
Leaf 3))
= Node (Node (Leaf 1,
Leaf 4),
Leaf 9))
(* etc. *)
in b0 && b1 && b2 && b3 && b4;;
Anakin (opening really big eyes): Is it possible to use this expressive power?The Supreme Chancellor: Not with a while loop.
In words:
- applying map_binary_tree to the successor function and a binary tree of integers should yield a binary tree that has the same shape as the given binary tree but where each of the payloads in the leaves is incremented by 1;
- applying map_binary_tree to the predecessor function and a binary tree of integers should yield a binary tree that has the same shape as the given binary tree but where each of the payloads in the leaves is decremented by 1; and
- applying map_binary_tree to the squaring function and a binary tree of integers should yield a binary tree that has the same shape as the given binary tree but where each of the payloads in the leaves is squared.
Since a map function implements a homomorphism (i.e., preserves the structure of its input), given a function and a binary tree, map_binary_tree copies this tree and applies this given function to the payload in each of the leaves:
let map_binary_tree f t =
(* map_binary_tree : ('a -> 'b) -> 'a binary_tree -> 'b binary_tree *)
let rec visit t =
match t with
| Leaf v ->
Leaf (f v)
| Node (t1, t2) ->
Node (visit t1, visit t2)
in visit t;;
And it passes the unit test too:
# test_map_binary_tree_int map_binary_tree;;
- : bool = true
#
The logical counterpart of the map function for binary trees¶
In the particular case where the function to map over a binary tree is a predicate (i.e., a Boolean-valued function), we often want to compute not the binary tree of its results but their conjunction or their disjunction:
let andmap_binary_tree p t =
(* andmap_binary_tree : ('a -> bool) -> 'a binary_tree -> bool *)
let rec visit t =
match t with
| Leaf v ->
p v
| Node (t1, t2) ->
visit t1 && visit t2
in visit t;;
let ormap_binary_tree p t =
(* ormap_binary_tree : ('a -> bool) -> 'a binary_tree -> bool *)
let rec visit t =
match t with
| Leaf v ->
p v
| Node (t1, t2) ->
visit t1 || visit t2
in visit t;;
These definitions embody Boolean short-cut evaluation, in that the first occurrence of an absorbing element (false for conjunction and true for disjunction) determines the result of the function, disregarding the remaining payloads in the tree. If that is a problem, just name the result of each recursive call with a let-expression, as in the accompanying resource file (see strict_andmap_binary_tree and strict_ormap_binary_tree):
# andmap_binary_tree (fun n -> if n < 0 then false else 1/0 = 0) (Node (Leaf ~-1, Leaf 1));;
- : bool = false
# strict_andmap_binary_tree (fun n -> if n < 0 then false else 1/0 = 0) (Node (Leaf ~-1, Leaf 1));;
Exception: Division_by_zero.
#
Exercise 30¶
The goal of this exercise is to study polymorphic binary trees where the payloads are stored in the nodes. For example:
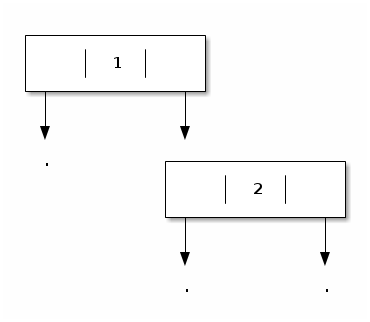
- Declare the data type of these polymorphic binary trees.
- Specify and implement a function that mirrors any given such binary trees.
Partial solution for Exercise 30¶
In this type,
- the leaves contain nothing and therefore their constructor is constant, and
- the payload is in the nodes and therefore their constructor takes a triple: the left subtree, the payload, and the right subtree.
Concretely:
type 'a binary_tree_with_payloads_in_the_nodes =
| Leaf_bare
| Node_with_payload of 'a binary_tree_with_payloads_in_the_nodes * 'a * 'a binary_tree_with_payloads_in_the_nodes;;
(The names “binary_tree_with_payloads_in_the_nodes”, “Leaf_bare”, and “Node_with_payload” are of our own choosing.)
The example depicted above is obtained by evaluating:
Node_with_payload
(Leaf_bare,
1,
Node_with_payload
(Leaf_bare,
2,
Leaf_bare))
Exercise 31¶
The goal of this exercise is to study polymorphic binary trees where the payloads are stored both in the leaves and in the nodes. For example:
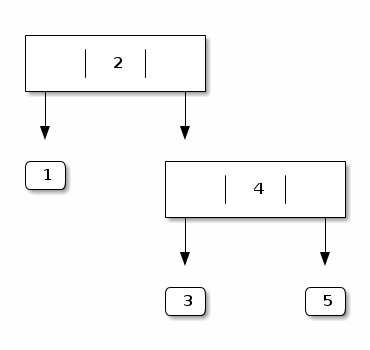
- Declare the data type of these polymorphic binary trees.
- As a continuation of Exercise 29, specify and implement a function that tests whether such a given binary tree of integers represents a well-balanced mobile.
Partial solution for Exercise 31¶
In this type,
- the leaves contain a payload and therefore their constructor takes an argument (namely the payload), and
- the nodes also contain a payload and therefore their constructor takes a triple: the left subtree, the payload, and the right subtree.
Concretely:
type 'a binary_tree_with_payloads_in_the_leaves_and_in_the_nodes =
| Leaf_with_payload of 'a
| Node_also_with_payload of 'a binary_tree_with_payloads_in_the_leaves_and_in_the_nodes * 'a * 'a binary_tree_with_payloads_in_the_leaves_and_in_the_nodes;;
(The names “binary_tree_with_payloads_in_the_leaves_and_in_the_nodes”, “Leaf_with_payload”, and “Node_also_with_payload” are of our own choosing.)
The example depicted above is obtained by evaluating:
Node_also_with_payload
(Leaf_with_payload 1,
2,
Node_also_with_payload
(Leaf_with_payload 3,
4,
Leaf_with_payload 5))
Alternative partial solution for Exercise 31¶
For more flexibility, we may want distinct types of payloads in the leaves and in the nodes:
type ('a, 'b) binary_tree_alt =
| Leaf_alt of 'a
| Node_alt of ('a, 'b) binary_tree_alt * 'b * ('a, 'b) binary_tree_alt;;
To wit:
# Node_alt (Leaf_alt 1, "2", Node_alt (Leaf_alt 3, "4", Leaf_alt 5));;
- : (int, string) binary_tree_alt = Node_alt (Leaf_alt 1, "2", Node_alt (Leaf_alt 3, "4", Leaf_alt 5))
#
The accompanying resource file also contains
- a function that maps a binary tree of type ('a, 'a) binary_tree_alt to a binary tree of type 'a binary_tree_with_payloads_in_the_leaves_and_in_the_nodes and
- a function that maps a binary tree of type 'a binary_tree_with_payloads_in_the_leaves_and_in_the_nodes to a binary tree of type ('a, 'a) binary_tree_alt.
Using structural induction, one can prove that these two functions are inverses of each other, which means that the two types ('a, 'a) binary_tree_alt and 'a binary_tree_with_payloads_in_the_leaves_and_in_the_nodes are isomorphic.
Resources¶
- The OCaml code for the present lecture note (latest version: 02 Apr 2020).
Version¶
Fixed two typos in the narrative, thanks to Syed Muhammad Maaz’s eagle eye [09 May 2020]
Updated the accompanying resource file to reflect the additions [02 Apr 2020]
Added the partial solutions for Exercises 30 and 31 [02 Apr 2020]
Regrouped [24 Mar 2020]
Fixed three typos in the narrative, thanks to Yunjeong Lee’s eagle eye [11 Jun 2019]
Added the section about map_binary_tree [31 Mar 2019]
Fixed a typo in the unit-test function for well-balanced mobile, thanks to Juwon Lee’s eagle eye [30 Mar 2019]
Completed with exercises [30 Mar 2019]
Updated [29 Mar 2019]
Created [28 Mar 2019]