Concrete data types

The goal of this lecture note is to describe how to declare new types in OCaml.

Resources

• The OCaml code for the present lecture note (latest version: 14 Mar 2020).

Declaring new types in OCaml

OCaml also lets us declare new types, be it

• to alias a pre-existing type,
• to name a compound type, or
• to define a sum type.

This expressive power is accounted for by the following refined BNF:

<toplevel-expression> ::= <expression>
                        | let <formal> = <definiens>
                        | type <variable> = <type-definiens>

<type-definiens>      ::= <type>
                        | {| <constructor> {of <type>}?}

<type>                ::= <variable>
                        | <type>{ * <type>}*
                        | <type> -> <type>

Let us study each of these constructs in turn.

Aliasing a pre-existing type

Say that we want to define a type to represent names, and that concretely this representation is that of strings. We could keep it in mind and mentally read “name” whenever we come across a string. However, that is not convenient since not all strings represent names. So instead, we can alias strings with the following type declaration:

type name = string;;

This declaration puts us in position to use name as a type. It extends the current type environment with a new binding, just like a let-expression extends the current value environment with a new binding.

Aliasing a compound type

For convenience, we can alias the type of Boolean transformers:

type boolean_transformer : bool -> bool;;

Likewise, say that we need to associate names and integers by pairing them:

name * int

For convenience, we can declare this assocation as such:

type association = name * int;;

More complex examples can be found in Exercise 4:

type triple_of_int_and_char_and_bool = int * char * bool;;

type pair_of_pair_of_int_and_bool_and_of_triple_of_char_and_string_and_char = (int * bool) * (char * string * char);;

Aliasing a polymorphic type

To alias a polymorphic type, one prefixes its type declaration with the corresponding type variables. For example:

type 'a singleton = 'a;;

type ('a, 'b) pair = 'a * 'b;;

type ('a, 'b, 'c) triple = 'a * 'b * 'c;;

Power and limitations of aliasing types

Aliasing types can clarify things but OCaml, left to itself, does not use our aliases unless we tell it to. To wit, the type of the swap function, fun (x, y) -> (y, x) is 'a * 'b -> 'b * 'a, not ('a, 'b) pair -> ('b, 'a) pair:

# fun (x, y) -> (y, x);;
- : 'a * 'b -> 'b * 'a = <fun>
#

Type constructors

To tell OCaml which type we mean, we declare these types so that they have type constructors:

type 'a singleton =
  | Singleton of 'a;;

type ('a, 'b) pair =
  | Pair of 'a * 'b;;

type ('a, 'b, 'c) triple =
  | Triple of 'a * 'b * 'c;;

These three declarations have the effect of extending the BNF of types with three new types, and the language of terms with three new constructors:

SINGLETON	G |- e : t
	G |- Singleton e : t singleton

PAIR	G |- e1 : t1	G |- e2 : t2
	G |- Pair (e1, e2) : (t1, t2) pair

TRIPLE	G |- e1 : t1	G |- e2 : t2	G |- e3 : t3
	G |- Triple (e1, e2, e3) : (t1, t2, t3) triple

The three type constructors Singleton, Pair, and Triple can now be used:

# Singleton 10;;
- : int singleton = Singleton 10
# Pair (true, "hello");;
- : (bool, string) pair = Pair (true, "hello")
#

And now the swap function can have a meaningful type that involves pairs:

# fun (Pair (x, y)) -> Pair (y, x);;
- : ('a, 'b) pair -> ('b, 'a) pair = <fun>
#

Analysis:

• the formal parameter, (Pair (x, y)), tells OCaml that the argument is expected to be constructed with the Pair constructor, and that the components of this pair should be named x and y; and
• the body of the function, Pair (y, x), tells OCaml to construct a pair out of y and x and to let this pair have the type pair.

The swap function expects a pair constructed using Pair:

# let swap (Pair (x, y)) = Pair (y, x);;
val swap : ('a, 'b) pair -> ('b, 'a) pair = <fun>
# swap (Pair (1, true));;
- : (bool, int) pair = Pair (true, 1)
#

The polymorphic option type

We have programmed several partial functions – functions that are only defined over part of their input (see Section Partial functions – a reminder in the lecture notes of Week 03). For example, the factorial function and the fibonacci function are only defined over non-negative integers. We implemented these partial functions as impure functions in OCaml:

let fac n =
 (* fac : int -> int *)
  let () = assert (n >= 0) in
  let rec loop n a =
    if n = 0
    then a
    else loop (pred n) (n * a)
  in loop n 1;;

let fib n =
 (* fib : int -> int *)
  let () = assert (n >= 0) in
  let rec visit n =
    if n = 0
    then (0, 1)
    else let n' = n - 1
         in let (fib_n', fib_n) = visit n'
            in (fib_n, fib_n' + fib_n)
  in let (fib_n, fib_succ_n) = visit n
     in fib_n;;

Applying them to a negative integer raises an error.

OCaml’s type system does not help us here because it only offers the type of integers, not the type of natural numbers.

But what if it could?

OCaml offers a type construct called an “option type” to account for such partial functions and implement them as total functions (see Section Total functions – a reminder in the lecture notes of Week 03). The option type has two constructors, None, which is nullary (i.e., that takes no arguments), and Some, which is unary (i.e., that takes one argument). It is predefined in OCaml.

Using this option type, we can implement total versions of the factorial and fibonacci functions as pure OCaml functions:

let pure_fac n =
 (* pure_fac : int -> int option *)
  if n < 0
  then None
  else Some (fac n);;

let pure_fib n =
 (* pure_fib : int -> int option *)
  if n < 0
  then None
  else Some (fib n);;

Whereas fac has type int -> int, pure_fac has type int -> int option, and it is well defined on all integers, whether negative, zero, or positive. (“Well defined” means that applying fac to any integer will return a value.)

Exercise 24

The goal of this exercise is to implement a function that returns the last element of a list, if any:

let test_list_last_int candidate =
  let b0 = (candidate [] = None)
  and b1 = (candidate [1] = Some 1)
  and b2 = (candidate [1; 2] = Some 2)
  and b3 = (candidate [1; 2; 3] = Some 3)
  (* etc. *)
  in b0 && b1 && b2 && b3;;

1. Use ordinary recursion over the given list.
2. Use fold_right_list.
3. What would happen if you used fold_left_list instead of fold_right_list in your second definition? Explain.

Analysis of Exercise 24, in the form of an interlude

Alfrothul: I know! I know!

Halcyon: Ah, Cloud Atlas...

Harald (patiently): What do you know now?

Alfrothul: I know how to program this function, look:

let list_last_int vs_given =
  let rec visit vs =
    match vs with
    | [] ->
       None
    | v :: vs' ->
       if vs' = []
       then Some v
       else visit vs'
  in visit vs_given;;

Vigfus (helpful as ever): And it passes the unit test too:

# test_list_last_int list_last_int;;
- : bool = true
#

Harald: What’s the type of your function?

Alfrothul: Easy-peasy:

# list_last_int;;
- : 'a list -> 'a option = <fun>
#

Harald: It’s a polymorphic type.

Alfrothul: Well, yes.

Harald: So why the name list_last_int?

Alfrothul: Drat. Right, the first unit-test function is named test_list_last_int, but of course that is because it has to be monomorphic. OK, let me rename this function, and add another unit-test function to boot:

let list_last vs_given =
  let rec visit vs =
    match vs with
    | [] ->
       None
    | v :: vs' ->
       if vs' = []
       then Some v
       else visit vs'
  in visit vs_given;;

let test_list_last_char candidate =
  let b0 = (candidate [] = None)
  and b1 = (candidate ['a'] = Some 'a')
  and b2 = (candidate ['a'; 'b'] = Some 'b')
  and b3 = (candidate ['a'; 'b'; 'c'] = Some 'c')
  (* etc. *)
  in b0 && b1 && b2 && b3;;

Vigfus: Good news, it still passes the first unit test, and it passes the new unit test too:

# test_list_last_int list_last;;
- : bool = true
# test_list_last_char list_last;;
- : bool = true
#

Alfrothul: Thank you very much.

Harald: Your definition doesn’t look right.

Alfrothul: Well, it passes the unit tests.

Harald: For sure, but it is testing vs' in the cons-case.

Alfrothul: Well, yes it does. It’s, like, its raison d’être.

Halcyon: Alfrothul, you are so full of joie de vivre.

Jacques Clouseau: What is all this French speaking all of a sudden?

Harald (heedlessly): How would you write it using fold_right_list? What is its inductive specification?

Alfrothul: Give me a chance:

let list_last vs =
  let rec visit vs =
    match vs with
    | [] ->
       None
    | v :: [] ->
       Some v
    | v :: vs' ->
       visit vs'
  in visit vs;;

Harald: Three clauses now? But there are only two list constructors. Plus, match-expressions are desugared into nested if-expressions, so your two definitions are the same.

Alfrothul: Harumph.

Brynja: Hi guys. You look challenged.

Halcyon: Only temporarily.

Harald: We need to define the last element of the list denoted by vs by structural induction over this list.

Brynja: I see.

Alfrothul: The base case: vs = [] first. There is no element in the empty list, and therefore no last element either. So the result must be None.

Brynja: The induction step: vs = v :: vs' now. The induction hypothesis over vs' is either Some v' (in which case the last element of vs' is v') or None (in which case vs' has no last element). And then the question is, in each case, what is the last element of v :: vs'?

Harald: Well, under the hypothesis that the last element of vs' is v', I guess that the last element of v :: vs' is still v'. The last shall remain the last, or something. So the result must also be Some v'.

Alfrothul: And under the hypothesis that vs' has no element, v is not only the first element of v :: vs', but its only element, and therefore also its last. The first shall be the last in a singleton list, or something. So the result must be Some v.

Vigfus: And that’s it?

Halcyon: Je vous l’avais bien dit les gars.

Alfrothul: Yes, you had told us, but still, let me see:

let list_last vs =
  let rec visit vs =
    match vs with
    | [] ->
       None
    | v :: vs' ->
       match visit vs' with
       | None ->
          Some v
       | Some v' ->
          Some v'
  in visit vs;;

Vigfus (swift): Good news, it passes the unit tests:

# test_list_last_int list_last;;
- : bool = true
# test_list_last_char list_last;;
- : bool = true
#

Harald: And now it is simple to express using fold_right_list, look:

let list_last_alt vs =
  fold_right_list None
                  (fun v ih ->
                    match ih with
                    | None ->
                       Some v
                    | Some v' ->
                       Some v')
                  vs;;

Vigfus: Well, believe it or not, this one also passes the unit tests:

# test_list_last_int list_last_alt;;
- : bool = true
# test_list_last_char list_last_alt;;
- : bool = true
#

Alfrothul: So that’s the solution?

Mimer: That’s a solution. But is it a nice solution?

Brynja: I guess not, considering the option-typed value that is tested each time visit returns.

Harald: You mean there is a solution where visit directly returns the last element, not the last element, optionally?

Mimer: Yup.

Brynja: Can you be less elliptic?

Mimer: Yes.

Brynja: Pray be.

Mimer: Less elliptic?

Brynja: Less elliptic.

Mimer: Well, look at the unit-test function.

Brynja (soberly): Looking here:

let test_list_last_char candidate =
  let b0 = (candidate [] = None)
  and b1 = (candidate ['a'] = Some 'a')
  and b2 = (candidate ['a'; 'b'] = Some 'b')
  and b3 = (candidate ['a'; 'b'; 'c'] = Some 'c')
  (* etc. *)
  in b0 && b1 && b2 && b3;;

Mimer: And?

Brynja: Well, there are two cases.

Vigfus (helpfully): The result is optional, so yes, there are two cases: None or Some v, where v is the last element of the given list.

Harald: None is used when the given list is empty, and Some when the given list is not empty.

Alfrothul: Guys, that’s something we can do a priori:

let list_last vs_given =
  match vs_given with
  | [] ->
     None
  | v :: vs ->
     Some ...;;

Halcyon (cleverly): You just wrote an ellipsis. Is that less elliptic?

Harald (heedless): Ah... Now we can declare and use a recursive function that traverses the tail of given list, since it is nonempty.

Alfrothul: And this recursive function takes two arguments – the current tail of the given list, to be traversed, and the element that precedes this current list in the given list.

Harald: I kind of see how to implement this recursive function, but how are we then going to express it using fold_right_list?

Mimer: You guys are doing good. Keep thinking.

Brynja: The same pattern applies to test whether a given list of integers is sorted, doesn’t it?

Mimer (soberly): Smiling here.

Declaring a sum type

Booleans, being either true or false, provide a prototypical example of a sum type. OCaml being implemented in OCaml, the type for Booleans is initially defined as follows:

type boolean = True
             | False;;

This declaration extends the current type environment with a new bindings and the language with two new data constructors: the type boolean now exists, together with its two constructors, True and False.

Notes:

• in actuality, boolean is called bool and its two constructors are literals in OCaml (namely the lexical units true and false);

• by lexical convention, types are written in lower case and data constructors are capitalized; and

• in the definition of a sum type, the vertical bar before the first constructor is optional. So one could also write:

  type boolean =
    | True
    | False;;
  

To decide which summand (i.e., which of True or False) one is given, one uses a match-expression. For example, here is an unparsing function for values of type boolean:

let show_boolean b =
 (* show_boolean : boolean -> string *)
  match b with
  | True -> "True"
  | False -> "False";;

And here are conversion functions between bool and boolean:

let boolean_to_bool b =
 (* boolean_to_bool : boolean -> bool *)
  match b with
  | True -> true
  | False -> false;;

let bool_to_boolean b =
 (* bool_to_boolean : bool -> boolean *)
  match b with
  | true -> True
  | false -> False;;

The match-expression enumerates all the possible constructors, and selects which one it is being given:

# bool_to_boolean true;;
- : boolean = True
# bool_to_boolean false;;
- : boolean = False
# boolean_to_bool True;;
- : bool = true
# boolean_to_bool False;;
- : bool = false
#

Truth be told, a match-expression in OCaml is merely an abbreviation for an if-expression, so bool_to_boolean can be equivalently declared with an if-expression:

let bool_to_boolean' b =
 (* bool_to_boolean' : bool -> boolean *)
  if b
  then True
  else False;;

So for example, we can implement two versions of the negation function over values of type boolean – either directly, or indirectly by detouring via the bool type:

let test_boolean_not candidate =
 (* test_boolean_not : (boolean -> boolean) -> bool *)
  let b0 = (candidate True = False)
  and b1 = (candidate False = True)
  in b0 && b1;;

let direct_not b =
 (* direct_not : boolean -> boolean *)
  match b with
  | True -> False
  | False -> True;;

let indirect_not b =
 (* indirect_not : boolean -> boolean *)
  bool_to_boolean (not (boolean_to_bool b));;

Both versions pass the unit test:

# test_boolean_not direct_not;;
- : bool = true
# test_boolean_not indirect_not;;
- : bool = true
#

The idea of detouring is explored further in Exercise 25.

A side remark

In match-expressions, the vertical bar before the first constructor is optional. So each of the following definitions is syntactically correct:

let minimum i j =
 (* minimum : int -> int -> bool *)
  match i < j with
  | true -> i    (* with a vertical bar before true *)
  | false -> j;;

let maximum i j =
 (* maximum : int -> int -> bool *)
  match i < j with
    true -> j    (* without a vertical bar before true *)
  | false -> i;;

Harald (grumbling): How many more hairs are we going to split here?

Loki (serene): The gods are in the details, Harald.

A useful sum type with 3 constructors

Often, when comparing two ordered values v1 and v2, we need to distinguish 3 cases:

• v1 < v2
• v1 = v2
• v1 > v2

To this end, we nest two conditional expressions, and the resulting layout is not very pleasing to the eye.

Instead, we can define a sum type that captures this comparison:

type comparison = Lt | Eq | Gt;;

let compare v1 v2 =
 (* compare : 'a -> 'a -> comparison *)
  if v1 < v2 then Lt else if v1 = v2 then Eq else Gt;;

And now the program layout is more pleasing to the eye and therefore readable:

match compare v1 v2 with
| Lt ->
   ...
| Eq ->
   ...
| Gt ->
   ...

Beware of the Turing tar-pit

in which everything is possible

but nothing of interest is easy.

—Alan Perlis‘s programming epigram #54

Declaring a sum type, continued

So sum types are declared by enumerating its constructors. These constructors can be parameterized. For example, here is the sum type for integers and strings:

type integer_or_string =
| Integer of int
| String of string;;

For example, here is an unparsing function for values of type integer_or_string:

let show_integer_or_string v =
 (* show_integer_or_string : integer_or_string -> string *)
  match v with
  | Integer n -> "Integer " ^ show_int n
  | String s -> "String " ^ show_string s;;

Likewise here are two predicates to test whether a value of type integer_or_string is an integer or a string:

let is_integer v =
 (* is_integer : integer_or_string -> bool *)
  match v with
  | Integer n -> true
  | String s -> false;;

let is_string v =
 (* is_string : integer_or_string -> bool *)
  match v with
  | Integer n -> false
  | String s -> true;;

The option type, revisited

The option type (see Section The polymorphic option type just above) is predefined in OCaml, but still here its definition anyhow:

type 'a option =
| Some of 'a
| None;;

Applying the constructor Some to a value of type t yields a value of type t option:

# Some 33;;
- : int option = Some 33
# Some true;;
- : bool option = Some true
# Some "thing or other";;
- : string option = Some "thing or other"
# Some (Some (Some "stuttering"));;
- : string option option option = Some (Some (Some "stuttering"))
#

The list type, revisited

The list type is predefined in OCaml, but still here a definition anyhow:

type 'a homemade_list =
| Nil
| Cons of 'a * 'a homemade_list;;

Using these two constructors, we can construct our own lists:

# Nil;;
- : 'a homemade_list = Nil
# Cons (1, Nil);;
- : int homemade_list = Cons (1, Nil)
# Cons (2, Cons (1, Nil));;
- : int homemade_list = Cons (2, Cons (1, Nil))
# Cons ("2", Cons ("1", Nil));;
- : string homemade_list = Cons ("2", Cons ("1", Nil))
#

Exercise 25

Here is the type of polymorphic right-to-left lists (hereby: “tsils”):

type 'a tsil =
| Lin
| Snoc of 'a tsil * 'a;;

Halcyon: On behalf of all the left-handed people in the world, thank you.

For example, evaluating Snoc (Snoc (Lin, 1), 2) gives rise to the following construct, where Lin is depicted with ][ and Snoc with a box with two entries:

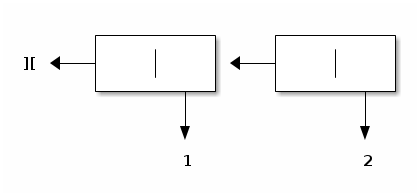
1. Specify and implement a htgnel function that computes the length of a tsil in the same manner as length computes the length of a list.

2. Specify and implement a dneppa function that computes the concatenation of two tsils in the same manner as append computes the concatenation of two lists.

3. Specify and implement a pam_tsil function that maps a function to each of the elements of a tsil and construct the tsil of the results, in the same manner as map_list maps a function to each of the elements of a list and construct the corresponding list with the results.

4. Implement two versions of a esrever function that reverses a tsil: one without an accumulator that uses dneppa, and one with an accumulator that only uses Snoc.

5. Specify and implement two conversion functions list_to_tsil and tsil_to_list that convert lists to tsils and vice versa:

   let test_list_to_tsil candidate =
     let b0 = (candidate [] = Lin)
     and b2 = (candidate (2 :: 1 :: []) = Snoc (Snoc (Lin, 1), 2))
     (* etc. *)
     in b0 && b2;;
   
   let test_tsil_to_list candidate =
     let b0 = (candidate Lin = [])
     and b2 = (candidate (Snoc (Snoc (Lin, 1), 2)) = 2 :: 1 :: [])
     (* etc. *)
     in b0 && b2;;
   

Vigfus: It is at moments like this that I am glad we don’t have an oral exam here.

6. Using list_to_tsil and tsil_to_list, implement
   • htgnel in terms of length,
   • length in terms of htgnel,
   • pam_tsil in terms of map_list, and
   • map_list in terms of pam_tsil.

7. Time permitting, implement the tsil counterparts of fold_right_list and of fold_left_list.

Prelude

Harald: A prelude at the end of a lecture note, now.

Brynja: Unless this ‘lude is meant to be read before embarking on Exercise 25?

Alfrothul: That could well be.

Brynja: Well, along the same line, and since time is short, I think we should start this exercise with its last question.

Harald (O_o): Its last question.

Brynja: Well, yes – start by implementing list_to_tsil and tsil_to_list.

Alfrothul: Why?

Brynja: Well, because tsils are the right-to-left analogue of lists – and vice versa), and therefore it only makes sense that what a function does on lists, its analogue should do on tsils, and vice versa too. Look:

let make_tsil_to_tsil_analogue f =
 (* make_tsil_to_tsil_analogue : ('a list -> 'b list) -> 'a tsil -> 'b tsil *)
  fun sv -> list_to_tsil (f (tsil_to_list sv));;

let make_list_to_list_analogue f =
 (* make_list_to_list_analogue : ('a tsil -> 'b tsil) -> 'a list -> 'b list *)
  fun vs -> tsil_to_list (f (list_to_tsil vs));;

Harald: Oh. You mean that esrever should do the analogue of reverse, for example?

Brynja: Sure do:

# make_tsil_to_tsil_analogue List.rev (Snoc (Snoc (Snoc (Lin, 3), 2), 1));;
- : int tsil = Snoc (Snoc (Snoc (Lin, 1), 2), 3)
#

Harald: I see – applying the tsil analogue of the reverse function to the tsil analogue of a list yields the tsil analogue of the reverse of this list.

Halcyon (cringing): Headache!

Vigfus (beaming): This is _so_ convenient for writing our unit tests.

Alfrothul: Actually, the same idea works for functions that produce lists or tsils:

let make_to_tsil_analogue f =
  (* make_to_tsil_analogue : ('a -> 'b list) -> 'a -> 'b tsil *)
  fun v -> list_to_tsil (f v);;

let make_to_list_analogue f =
  (* make_to_list_analogue : ('a -> 'b tsil) -> 'a -> 'b list *)
  fun v -> tsil_to_list (f v);;

Brynja: Yup. Applying make_to_tsil_analogue to atoi, for example, yields a function that maps a non-negative integer to the tsil of its successive predecessors.

Harald: Ditto for functions that take lists as input, and tsils too:

let make_tsil_to_analogue f =
 (* make_tsil_to_analogue : ('a list -> 'b) -> 'a tsil -> 'b *)
 fun sv -> f (tsil_to_list sv);;

let make_list_to_analogue f =
  (* make_list_to_analogue : ('a tsil -> 'b) -> 'a list -> 'b *)
  fun vs -> f (list_to_tsil vs);;

Vigfus: You were right, this prelude should be read before embarking on Exercise 25.

Mutually recursive types

Just as functions can be defined in a mutually recursive fashion (e.g., the even / odd predicates over natural numbers are defined in terms of each other), types can be defined in a mutually recursive fashion using the and keyword.

[...]

Resources

• The OCaml code for the present lecture note (latest version: 14 Mar 2020).

Version

Added the section about A useful sum type with 3 constructors [02 Apr 2020]

Expanded the interlude [02 Apr 2020]

Sketched the section about mutually recursive types [02 Apr 2020]

Created [14 Mar 2020]