Imperative lists¶
The goal of this lecture note is to study imperative lists, i.e., lists whose tails are mutable:
type 'a ilist = Inil
| Icons of 'a * 'a ilist ref;;
Resources¶
- The OCaml code for the present lecture note (latest version: 10 Apr 2020).
Warmup¶
The empty list is constructed by evaluating Inil and is depicted as follows:
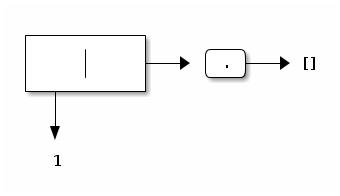
The singleton list containing 1 is constructed by evaluating Icons (1, ref Inil) and is depicted as follows:
The 2-elements list containing 2 and then 1 is constructed by evaluating Icons (2, ref (Icons (1, ref Inil))) and is depicted as follows:

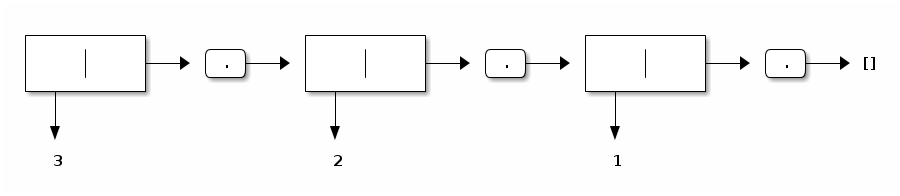
The 3-elements list containing 3, and then 2, and then 1 is constructed by evaluating Icons (3, ref (Icons (2, ref (Icons (1, ref Inil))))) and is depicted as follows:
The tail of each successive sublist is a mutable reference, and therefore can be mutated to point to another imperative list.
Unparsing imperative lists¶
Let us unparse imperative lists and render them as ordinary lists. Since imperative lists can be arbitrarily long, let us parameterize the unparsing function with a length:
let test_show_ilist_int candidate =
let b0 = (candidate Inil 10
= "[]")
and b1 = (candidate (Icons (1, ref Inil)) 10
= "[1]")
and b2 = (candidate (Icons (2, ref (Icons (1, ref Inil)))) 10
= "[2; 1]")
and b3 = (candidate (Icons (3, ref (Icons (2, ref (Icons (1, ref Inil)))))) 10
= "[3; 2; 1]")
and b4 = (candidate (Icons (3, ref (Icons (2, ref (Icons (1, ref Inil)))))) 2
= "[3; 2; ...")
and b5 = (candidate (Icons (3, ref (Icons (2, ref (Icons (1, ref Inil)))))) 1
= "[3; ...")
in b0 && b1 && b2 && b3 && b4 && b5;;
The unparsing function is defined by mathematical induction over the length of the imperative list to unparse, with the proviso that this list might be shorter than the given length:
let show_ilist show_yourself ivs n =
assert (n >= 0);
match ivs with
| Inil ->
"[]"
| Icons (v, rivs') ->
let rec show_ilist_aux v ivs' n =
if n = 0
then "..."
else match ivs' with
| Inil ->
show_yourself v ^ "]"
| Icons (v', rivs'') ->
(show_yourself v) ^ "; " ^ (show_ilist_aux v' !rivs'' (pred n))
in "[" ^ show_ilist_aux v !rivs' n;;
This implementation passes the unit tests:
# test_show_ilist_int (show_ilist show_int);;
- : bool = true
#
For convenience when implementing further unit-test functions, let us also define two auxiliary functions for tracing:
let print_ilist show_yourself ivs n =
Printf.printf "%s\n" (show_ilist show_yourself ivs n);;
let print_ilist_int_fixed silent ivs =
if silent
then ()
else print_ilist show_int ivs 20;;
The last one is parameterized with a Boolean flag.
Circular lists¶
The raison d’être for imperative lists is the ability to construct circular lists such as the following ones:
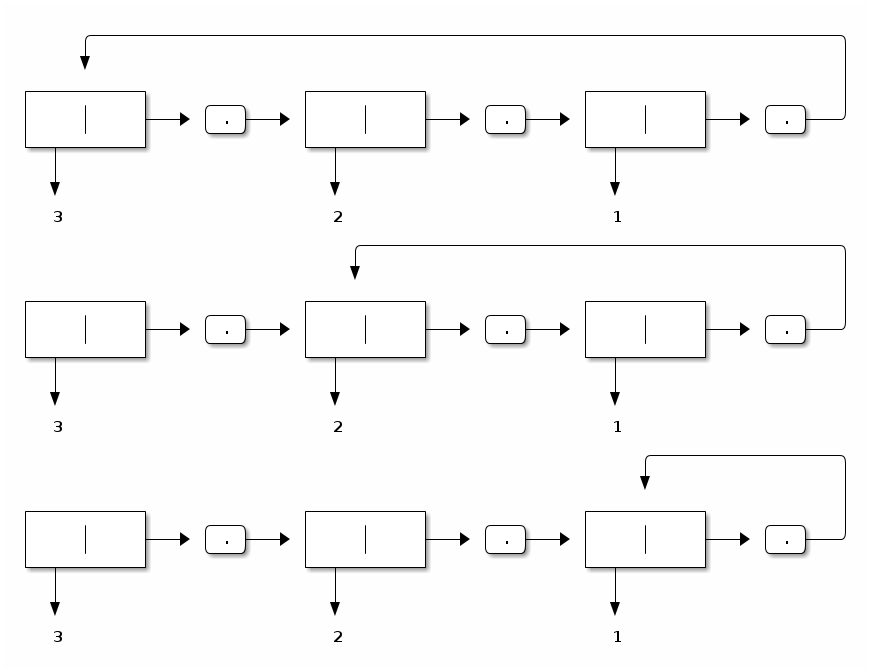
Computing with imperative lists raises a whole bunch of new challenges, because we can’t just traverse them recursively since they might be circular and therefore the traversal would not terminate.
The rest of this lecture note investigates
- how to construct circular lists,
- how to detect whether an imperative list is circular,
- how to compute the length of an imperative list, if it is not circular,
- how to abstract the corresponding programming pattern into two functionals, fold_right_ilist and fold_left_ilist that are respectively recursive and tail recursive with an accumulator, and
- how to use fold_right_ilist and fold_left_ilist to implement
functions that
- detect whether an imperative list is circular,
- compute the length of an imperative list, if it is not circular,
- concatenate an imperative list to another, if the first one is not circular,
- reverse an imperative list, if it is not circular, and
- map a function over the elements of an imperative list and yield the corresponding imperative list of results, if the given list is not circular.
This lecture note does not cover how to
- imperatively concatenate a (non-circular) list to another by mutating the last reference of the first list so that it points to the second,
- reverse an imperative list in place, so that its last pair becomes the first pair of the result, and its first pair becomes the last pair of the result, and
- map a function over a circular list into a corresponding circular list.
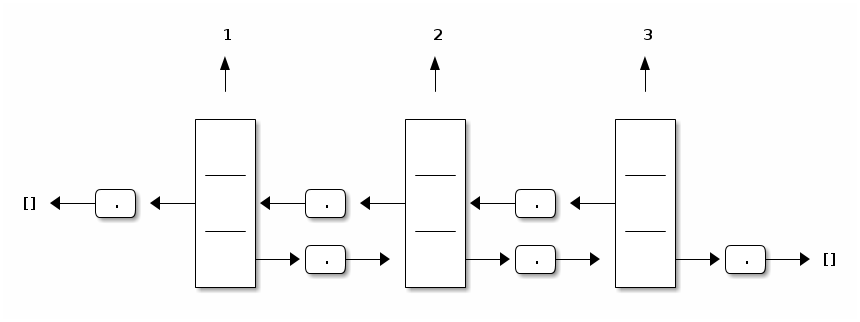
Also out of scope are imperative doubly linked lists, where each component of the list points both to the previous component of the list and to the following one:
type 'a idllist = Dnil
| Dcons of 'a * 'a idllist ref * 'a idllist ref;;
For example, the imperative doubly linked list containing 1, 2, and 3 is depicted as follows:
How to construct a circular list¶
To start, here is a question – how, using the ilist constructors, can one construct the following simplest circular list?
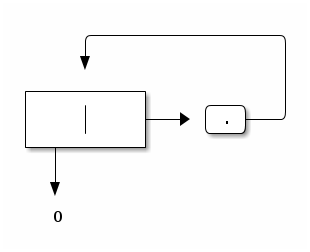
In other words, we need to write an OCaml expression such that evaluating it yields the value depicted above.
Interlude¶
Harald: That looks like a job for us.
Alfrothul: Let’s see. There is a pair, and there is a reference, so here is the skeleton of the expression:
Icons (1, ref ...)
Harald: Right. Now all we need is to replace ... by the name of the resulting value:
# let c = Icons (1, ref c);;
Characters 22-23:
let c = Icons (1, ref c);;
^
Error: Unbound value c
#
Alfrothul: Wait – we need to first name the value.
Harald: No, we first need to construct this value.
Loki: Which came first – the chicken or the egg?
Halcyon: You mean we need the Coq proof assistant?
Brynja: Guys, guys – this is a case for recursion:
let rec c = Icons (1, ref c)
Mimer: I am afraid you can’t do that – OCaml only lets us define recursive functions, not recursive values.
Brynja: Well, I don’t know about that:
# let rec c = Icons (1, ref c);;
val c : int ilist =
Icons (1,
{contents =
Icons (1,
{contents =
Icons (1,
{contents =
Icons (1,
{contents =
Icons (1,
{contents =
Icons (1,
{contents =
Icons (1,
{contents =
Icons (1,
{contents =
Icons (1,
{contents =
Icons (1,
{contents =
Icons (1,
{contents =
Icons (1,
{contents =
Icons (1,
{contents =
Icons (1,
{contents =
Icons (1,
{contents =
Icons (1,
{contents =
Icons (1,
{contents =
Icons (1,
{contents =
Icons (1,
{contents =
Icons (1,
{contents =
Icons (1,
{contents =
Icons (1,
{contents =
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons (1,
{contents
=
Icons
(...)})})})})})})})})})})})})})})})})})})})})})})})})})})})})})})})})})})})})})})})})})})})})})})})})})})
#
Mimer (smiling): I didn’t see this one coming. OK, that’s a feature. What I was expecting is a two-time process where first the value is constructed with a reference to Inil, and then this reference is mutated to the value:
let temporary_reference = ref Inil
in let temporary_value = Icons (1, temporary_reference)
in temporary_reference := temporary_value;
temporary_value;;
Brynja: Fair enough. You made the point that recursion can be implemented by self-reference, which requires sequencing and mutation.
A generic unit-test function for circular lists¶
In preparation for testing unary functions of type 'b ilist -> 'a, let us write a generic unit-test function for imperative lists of integers and parameterize it with the result that is expected if these lists are circular. The circular lists to be successively tested are the following ones.
iv0s, iv1s, iv2s, iv3s, iv4s, iv5s:

iv0s, iv1s, iv2s, iv3s, iv4s, iv5s:

iv0s, iv1s, iv2s, iv3s, iv4s, iv5s:

iv0s, iv1s, iv2s, iv3s, iv4s, iv5s:

iv0s, iv1s, iv2s, iv3s, iv4s, iv5s:

iv0s, iv1s, iv2s, iv3s, iv4s, iv5s:

The generic function is also parameterized with a Boolean flag so that we can visualize the successive lists as they are mutated:
let make_stress_test_int result silent candidate =
(* make_stress_test_int: 'a -> bool -> (int ilist -> 'a) -> bool *)
let join = ref Inil
in let iv0s = Icons (0, join)
in let iv1s = Icons (1, ref iv0s)
in let iv2s = Icons (2, ref iv1s)
in let iv3s = Icons (3, ref iv2s)
in let iv4s = Icons (4, ref iv3s)
in let iv5s = Icons (5, ref iv4s)
in print_ilist_int_fixed silent iv5s;
join := iv0s;
print_ilist_int_fixed silent iv5s;
let b00 = (candidate iv0s = result)
and b01 = (candidate iv1s = result)
and b02 = (candidate iv2s = result)
and b03 = (candidate iv3s = result)
and b04 = (candidate iv4s = result)
and b05 = (candidate iv5s = result)
in join := iv1s;
print_ilist_int_fixed silent iv5s;
let b10 = (candidate iv0s = result)
and b11 = (candidate iv1s = result)
and b12 = (candidate iv2s = result)
and b13 = (candidate iv3s = result)
and b14 = (candidate iv4s = result)
and b15 = (candidate iv5s = result)
in join := iv2s;
print_ilist_int_fixed silent iv5s;
let b20 = (candidate iv0s = result)
and b21 = (candidate iv1s = result)
and b22 = (candidate iv2s = result)
and b23 = (candidate iv3s = result)
and b24 = (candidate iv4s = result)
and b25 = (candidate iv5s = result)
in join := iv3s;
print_ilist_int_fixed silent iv5s;
let b30 = (candidate iv0s = result)
and b31 = (candidate iv1s = result)
and b32 = (candidate iv2s = result)
and b33 = (candidate iv3s = result)
and b34 = (candidate iv4s = result)
and b35 = (candidate iv5s = result)
in join := iv4s;
print_ilist_int_fixed silent iv5s;
let b40 = (candidate iv0s = result)
and b41 = (candidate iv1s = result)
and b42 = (candidate iv2s = result)
and b43 = (candidate iv3s = result)
and b44 = (candidate iv4s = result)
and b45 = (candidate iv5s = result)
in join := iv5s;
print_ilist_int_fixed silent iv5s;
let b50 = (candidate iv0s = result)
and b51 = (candidate iv1s = result)
and b52 = (candidate iv2s = result)
and b53 = (candidate iv3s = result)
and b54 = (candidate iv4s = result)
and b55 = (candidate iv5s = result)
in let b0 = b00 && b01 && b02 && b03 && b04 && b05
and b1 = b10 && b11 && b12 && b13 && b14 && b15
and b2 = b20 && b21 && b22 && b23 && b24 && b25
and b3 = b30 && b31 && b32 && b33 && b34 && b35
and b4 = b40 && b41 && b42 && b43 && b44 && b45
and b5 = b50 && b51 && b52 && b53 && b54 && b55
in b0 && b1 && b2 && b3 && b4 && b5;;
To visualize the successive lists, we can instantiate the generic function at string type:
# make_stress_test_int "whatever" false (fun _ -> "some string or another");;
[5; 4; 3; 2; 1; 0]
[5; 4; 3; 2; 1; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; ...
[5; 4; 3; 2; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; ...
[5; 4; 3; 2; 1; 0; 2; 1; 0; 2; 1; 0; 2; 1; 0; 2; 1; 0; 2; 1; ...
[5; 4; 3; 2; 1; 0; 3; 2; 1; 0; 3; 2; 1; 0; 3; 2; 1; 0; 3; 2; ...
[5; 4; 3; 2; 1; 0; 4; 3; 2; 1; 0; 4; 3; 2; 1; 0; 4; 3; 2; 1; ...
[5; 4; 3; 2; 1; 0; 5; 4; 3; 2; 1; 0; 5; 4; 3; 2; 1; 0; 5; 4; ...
- : bool = false
#
And indeed the sample imperative list evolves from not being circular to
- being circular and pointing back at the node containing 0,
- being circular and pointing back at the node containing 1,
- being circular and pointing back at the node containing 2,
- being circular and pointing back at the node containing 3,
- being circular and pointing back at the node containing 4, and
- being circular and pointing back at the node containing 5.
How to detect whether an imperative list is circular: the unit-test functions¶
The stress-test function is immediate to write:
let stress_test_icircular_int =
make_stress_test_int true;;
Ditto for a unit-test function for finite imperative lists:
let test_icircular_int candidate =
let ivs = Inil
in let b0 = (candidate ivs = false)
and ivs = Icons (1, ref ivs)
in let b1 = (candidate ivs = false)
and ivs = Icons (2, ref ivs)
in let b2 = (candidate ivs = false)
and ivs = Icons (3, ref ivs)
in let b3 = (candidate ivs = false)
and ivs = Icons (4, ref ivs)
in let b4 = (candidate ivs = false)
in b0 && b1 && b2 && b3 && b4;;
How to detect whether an imperative list is circular: Take 0¶
As a first shot, let us program a function that uses an accumulator to list all the nodes that have been encountered before in the given imperative list: if a new node occurs in this list, the imperative list is circular. Otherwise, sooner or later, we will encounter the end of the imperative list:
let icircular_v0 ivs =
let occurs ivs ivss =
let rec traverse ivss =
match ivss with
| [] ->
false
| ivs' :: ivss' ->
if ivs == ivs' (* <-- physical equality *)
then true
else traverse ivss'
in traverse ivss
in let rec loop ivs a =
match ivs with
| Inil ->
false
| Icons (v, rivs') ->
if occurs ivs a
then true
else loop !rivs' (ivs :: a)
in loop ivs [];;
This implementation passes the unit tests:
# test_icircular_int icircular_v0;;
- : bool = true
# stress_test_icircular_int true icircular_v0;;
- : bool = true
#
As for its computational complexity, it is linear in space, due to the accumulated list of the successive nodes, and it is quadratic in time, due to the successive traversals of the accumulator, which grows at each iteration.
How to detect whether an imperative list is circular: Take 1¶
There is actually no need for the accumulator, since the given list already contains the nodes that have been encountered so far. We however need to keep a count of the nodes traversed so far, to distinguish between the end of the test and the actual detection of a circularity:
exception Impossible_case of string;;
let icircular_v1 ivs_init =
let occurs ivs_current n_current =
let rec traverse ivs n =
if ivs == ivs_current (* <-- physical equality *)
then if n = n_current
then false
else true
else match ivs with
| Inil ->
raise (Impossible_case "icircular_v1")
| Icons (_, rivs') ->
traverse !rivs' (succ n)
in traverse ivs_init 0
in let rec loop ivs n =
match ivs with
| Inil ->
false
| Icons (_, rivs') ->
if occurs ivs n
then true
else loop !rivs' (succ n)
in loop ivs_init 0;;
In the definition of occurs, the Inil case is impossible because traverse is applied to a suffix of the given imperative list.
This implementation passes the unit tests:
# test_icircular_int icircular_v1;;
- : bool = true
# stress_test_icircular_int true icircular_v1;;
- : bool = true
#
As for its computational complexity, it is constant in space but it is still quadratic in time, due to the successive increasing traversals of the initial imperative list.
Programmatically, the implementation can be made to work iteratively by declaring occurs and loop as mutually tail-recursive functions and by supplying occurs with the two future parameters of loop:
let icircular_v2 ivs_init =
let rec occurs ivs_current n_current ivs_next n_next =
let rec traverse ivs n =
if ivs == ivs_current (* <-- physical equality *)
then if n = n_current
then loop ivs_next n_next
else true
else match ivs with
| Inil ->
raise (Impossible_case "icircular_v2")
| Icons (_, rivs') ->
traverse !rivs' (succ n)
in traverse ivs_init 0
and loop ivs n =
match ivs with
| Inil ->
false
| Icons (_, rivs') ->
occurs ivs n !rivs' (succ n)
in loop ivs_init 0;;
(The last parameter of occurs is unnecessary since it can be deduced from its second parameter.)
This implementation also passes the unit tests:
# test_icircular_int icircular_v2;;
- : bool = true
# stress_test_icircular_int true icircular_v2;;
- : bool = true
#
The computational complexity remains the same.
How to detect whether an imperative list is circular: Take 2¶
The following implementation is based on the two-pronged idea of
- a slow pointer to traverse the given imperative list one node at a time, and
- a fast pointer to traverse the given imperative list two nodes at a time.
If the fast pointer reaches Inil, the list is not circular. If the slow and the fast pointer refer to the same node, the list is circular:
exception Slow_pointer of string;;
let icircular_v3 ivs =
match ivs with
| Inil ->
false
| Icons (v, rivs') ->
let rec loop ivs iws =
if ivs == iws (* <-- physical equality *)
then true
else match ivs with
| Inil ->
false
| Icons (v, rivs') ->
match !rivs' with
| Inil ->
false
| Icons (v', rivs'') ->
match iws with
| Inil ->
raise (Slow_pointer "icircular_v3")
| Icons (w, riws') ->
loop !rivs'' !riws'
in loop !rivs' ivs;;
This implementation passes the unit tests:
# test_icircular_int icircular_v3;;
- : bool = true
# stress_test_icircular_int true icircular_v3;;
- : bool = true
#
How to compute the length of an imperative list¶
The stress-test function is immediate to write:
let stress_test_ilength_int =
make_stress_test_int None;;
Ditto for a unit-test function for finite imperative lists:
let test_ilength_int candidate =
let ivs = Inil
in let b0 = (candidate ivs = Some 0)
and ivs = Icons (1, ref ivs)
in let b1 = (candidate ivs = Some 1)
and ivs = Icons (2, ref ivs)
in let b2 = (candidate ivs = Some 2)
and ivs = Icons (3, ref ivs)
in let b3 = (candidate ivs = Some 3)
and ivs = Icons (4, ref ivs)
in let b4 = (candidate ivs = Some 4)
in b0 && b1 && b2 && b3 && b4;;
Let us reuse the idea of traversing the imperative list with both a slow pointer and a fast pointer:
let ilength_v0 ivs =
match ivs with
| Inil ->
Some 0
| Icons (v, rivs') ->
let rec loop ivs iws a =
if ivs == iws
then None
else match ivs with
| Inil ->
Some a
| Icons (v, rivs') ->
match !rivs' with
| Inil ->
Some (a + 1)
| Icons (v', rivs'') ->
match iws with
| Inil ->
raise (Slow_pointer "ilength_v0")
| Icons (w, riws') ->
loop !rivs'' !riws' (a + 2)
in loop !rivs' ivs 1;;
This implementation passes the unit tests:
# test_ilength_int ilength_v0;;
- : bool = true
# stress_test_ilength_int true ilength_v0;;
- : bool = true
#
Since the definition of ilength_v0 is very similar to that of icircular_v3, let us abstract their programming pattern into a fold-right function and a fold-left function.
How to fold right over imperative lists¶
Generalizing, let us abstract the Inil case, the Icons case, and the circularity case:
let fold_right_ilist inil_case icons_case circular_case ivs =
(* fold_right_ilist : 'a -> ('b -> 'a -> 'a) -> ('b -> 'a) -> 'b ilist -> 'a *)
match ivs with
| Inil ->
inil_case
| Icons (v, rivs') ->
let rec loop ivs iws =
if ivs == iws
then circular_case v
else match ivs with
| Inil ->
inil_case
| Icons (v, rivs') ->
icons_case v (match !rivs' with
| Inil ->
inil_case
| Icons (v', rivs'') ->
icons_case v' (loop !rivs'' (match iws with
| Inil ->
raise (Slow_pointer "fold_right_ilist")
| Icons (w, riws') ->
!riws')))
in icons_case v (loop !rivs' ivs);;
How to fold left over imperative lists¶
Likewise for the tail-recursive counterpart with an accumulator:
let fold_left_ilist inil_case icons_case circular_case ivs =
(* fold_left_ilist : 'a -> ('b -> 'a -> 'a) -> ('b -> 'a) -> 'b ilist -> 'a *)
match ivs with
| Inil ->
inil_case
| Icons (v, rivs') ->
let rec loop ivs iws a =
if ivs == iws
then circular_case v
else match ivs with
| Inil ->
a
| Icons (v, rivs') ->
match !rivs' with
| Inil ->
icons_case v a
| Icons (v', rivs'') ->
loop !rivs''
(match iws with
| Inil ->
raise (Slow_pointer "fold_left_ilist")
| Icons (w, riws') ->
!riws')
(icons_case v' (icons_case v a))
in loop !rivs' ivs (icons_case v inil_case);;
How to detect whether an imperative list is circular using fold-right¶
It is now simple to implement a predicate detecting whether an imperative list is circular, using fold_right_ilist:
let icircular_v4 ivs =
fold_right_ilist false (fun v ih -> ih) (fun v -> true) ivs;;
This implementation passes the unit tests:
# test_icircular_int icircular_v4;;
- : bool = true
# stress_test_icircular_int true icircular_v4;;
- : bool = true
#
How to detect whether an imperative list is circular using fold-left¶
And it is just as simple to implement a predicate detecting whether an imperative list is circular, using fold_left_ilist:
let icircular_v5 ivs =
fold_left_ilist false (fun v ih -> ih) (fun v -> true) ivs;;
This implementation passes the unit tests:
# test_icircular_int icircular_v5;;
- : bool = true
# stress_test_icircular_int true icircular_v5;;
- : bool = true
#
How to compute the length of an imperative list using fold-left¶
Ditto for computing the length of an imperative list, using fold_left_ilist:
let ilength_v1 ivs =
(* ilength_v1 : 'a ilist -> int option *)
fold_left_ilist (Some 0)
(fun v ih ->
match ih with
| None ->
None
| Some n ->
Some (succ n))
(fun _ -> None)
ivs;;
This implementation passes the unit tests:
# test_ilength_int ilength_v1;;
- : bool = true
# stress_test_ilength_int true ilength_v1;;
- : bool = true
#
How to compute the length of an imperative list using fold-right¶
For the same price, we can use fold_right_ilist:
let ilength_v2 ivs =
(* ilength_v2 : 'a ilist -> int option *)
fold_right_ilist (Some 0)
(fun v ih ->
match ih with
| None ->
None
| Some n ->
Some (succ n))
(fun _ -> None)
ivs;;
This implementation passes the unit tests:
# test_ilength_int ilength_v2;;
- : bool = true
# stress_test_ilength_int true ilength_v2;;
- : bool = true
#
How to compute the length of an imperative list using an exception¶
Rather than using an option type, we can raise an exception in case of a circularity:
exception Circular of string;;
let ilength_v3 ivs =
try Some (fold_right_ilist 0
(fun v ih -> succ ih)
(fun v -> raise (Circular "ilength_v3"))
ivs)
with
| Circular _ -> None;;
let ilength_v4 ivs =
try Some (fold_left_ilist 0
(fun v ih -> succ ih)
(fun v -> raise (Circular "ilength_v4"))
ivs)
with
| Circular _ -> None;;
Both implementations pass the unit tests.
How to concatenate two imperative lists¶
From the comfort of fold_right_ilist, it is simple to define an append function for imperative lists that is the analogue of the append function for lists:
let test_iappend_int candidate =
let b0 = (show_option (fun v -> show_ilist show_int v 10)
(candidate (Icons (4, ref (Icons (3, ref Inil))))
(Icons (2, ref (Icons (1, ref (Icons (0, ref Inil)))))))
= "Some [4; 3; 2; 1; 0]")
in b0;;
let iappend ixs iys =
try Some (fold_right_ilist iys
(fun v ih -> Icons (v, ref ih))
(fun v -> raise (Circular "iappend"))
ixs)
with
| Circular _ -> None;;
This implementation passes the unit tests:
# test_iappend_int iappend;;
- : bool = true
#
How to reverse an imperative list¶
From the comfort of fold_left_ilist, it is simple to define a reverse function for imperative lists that is the analogue of the reverse function for lists:
let test_ireverse_int candidate =
let b0 = (show_option (fun v -> show_ilist show_int v 10)
(candidate (Icons (1, ref (Icons (2, ref (Icons (3, ref Inil)))))))
= "Some [3; 2; 1]")
in b0;;
let ireverse ivs =
try Some (fold_left_ilist Inil
(fun v ih -> Icons (v, ref ih))
(fun v -> raise (Circular "ireverse"))
ivs)
with
| Circular _ -> None;;
This implementation passes the unit tests:
# test_ireverse ireverse;;
- : bool = true
#
How to map a function over an imperative list¶
From the comfort of fold_right_ilist, it is simple to define a map function for imperative lists that is the analogue of the map function for lists:
let test_imap_int candidate =
let b0 = (show_option (fun v -> show_ilist show_int v 10)
(candidate succ (Icons (1, ref (Icons (2, ref (Icons (3, ref Inil)))))))
= "Some [2; 3; 4]")
in b0;;
let imap f ivs =
try Some (fold_right_ilist Inil
(fun v ih -> Icons (f v, ref ih))
(fun v -> raise (Circular "imap"))
ivs)
with
| Circular _ -> None;;
This implementation passes the unit tests:
# test_imap imap;;
- : bool = true
#
Exercise 6¶
By analogy with Section Example: duplicating the elements of a list in Week 09, define a function that duplicates the elements of an imperative list, unit-test function and all.
Exercise 7¶
Define a function that, given two lists, prepends the reverse of the first to the second:
let test_prepend_reverse candidate = let b0 = (candidate [1; 2; 3] [4; 5; 6] = [3; 2; 1; 4; 5; 6]) in b0;;(Be a sport and do not use List.append nor List.rev.)
Define a function that, given two imperative lists, prepends the reverse of the first to the second.
(Be a sport and do not use iappend nor ireverse.)
Exercise 8¶
Define a function that, given two lists, prepends the first to the reverse of the second:
let test_postpend_reverse candidate = let b0 = (candidate [1; 2; 3] [4; 5; 6] = [1; 2; 3; 6; 5; 4]) in b0;;(Be a sport and do not use List.append nor List.rev.)
Define a function that, given two imperative lists, postpends the first to the reverse of the second.
(Be a sport and do not use iappend nor ireverse.)
Resources¶
- The OCaml code for the present lecture note (latest version: 10 Apr 2020).
Version¶
Fixed a typo in the definition of make_stress_test_int, thanks to Jonathan Chia’s eagle eye [10 Apr 2020]
Created [24 Mar 2020]