Exercises for Week 04

Exercise 0

1. At the top right and at the bottom right of the present page, there is a clickable word, “index”, to access the index of the current version of the lecture notes. Click on it and then peruse the index, making sure that its entries make sense to you (otherwise, click on them to check them out).

2. The lecture notes start with updates (Chapter Lecture Notes for Intro to CS, updates). Make sure to check them out regularly, as they reflect the development of the lecture.

3. Briefly explain, in your own words, the concept of commuting diagram, as presented in the postlude of Chapter Towards OCaml.

   For one more example (which could be connected to Exercise 7.i):

   

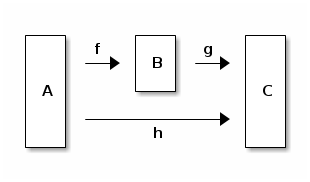
Mandatory exercises

• Exercise 0: perusing the index and checking the updates
• Exercise 5: implementing and testing exclusive disjunction
• Exercise 8 (from Week 03): exhibiting expressions of a given monomorphic type
• Exercise 6: exhibiting expressions of a given polymorphic type
• Exercise 7: exhibiting more expressions of a given polymorphic type
• Exercise 8: lexical scope at work
• Exercise 12: an all-too-common error
• Exercise 13 implementing and testing polynomials of degree 4
• Exercise 14: tinkering with the generator of random proofs
• Exercise 16: associating left and right

Recommended exercises

• Exercise 9: exhibiting even more expressions of a given type
• Exercise 11: a gorgeous unit-test function for string concatenation
• Exercise 15: implementing Strachey’s generator of love letters

Exercise for the over-achievers (this means you)

• Exercise 19: exhibiting a family of expressions of a family of given types; did we see these types before?

Exercise 16

A question about the design of OCaml:

• in its language of expressions, applications implicitly associate to the left, i.e., String.get "hello world" 0 is parsed as (String.get "hello world") 0;
• in its language of types, function types implicitly associate to the right, i.e., string -> int -> char is parsed as string -> (int -> char).

Justify this choice.

Hint: contemplate the APP typing rule.

Richard Feynman: I believe that has some significance for [y]our problem.

Mimer: Professor Feynman! Thanks for stopping by!

Exercise 17

Consider the following definition:

let length_of_string_self_concatenation s =
  String.length (s ^ s) = 2 * String.length s;;

What is the result of applying length_of_string_concatenation to any string?

• true, always?
• false, always?
• sometimes true, sometimes false?

Justify your answer.

Solution for Exercise 17

The answer is true, always, because concatenating a string to itself yields a string which is twice as long.

The computation carried out by length_of_string_self_concatenation can be depicted with the following commuting diagram:

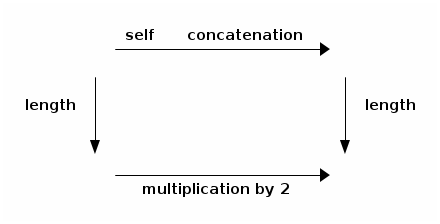
Exercise 18

Consider the following definition:

let length_of_string_concatenation s1 s2 =
  String.length (s1 ^ s2) = String.length s1 + String.length s2;;

What is the result of applying length_of_string_concatenation to any two strings?

• true, always?
• false, always?
• sometimes true, sometimes false?

Justify your answer.

Exercise 19

1. Exhibit an expression of type ('a * 'b * 'c * 'd * 'e -> 'f) -> unit -> 'a * 'b * 'c * 'd * 'e -> 'f. Justify your answer.
2. Exhibit an expression of type ('a * 'b * 'c * 'd * 'e -> 'f) -> 'a -> 'b * 'c * 'd * 'e -> 'f. Justify your answer.
3. Exhibit an expression of type ('a * 'b * 'c * 'd * 'e -> 'f) -> 'a * 'b -> 'c * 'd * 'e -> 'f. Justify your answer.
4. Exhibit an expression of type ('a * 'b * 'c * 'd * 'e -> 'f) -> 'a * 'b * 'c -> 'd * 'e -> 'f. Justify your answer.
5. Exhibit an expression of type ('a * 'b * 'c * 'd * 'e -> 'f) -> 'a * 'b * 'c * 'd -> 'e -> 'f. Justify your answer.
6. Exhibit an expression of type ('a * 'b * 'c * 'd * 'e -> 'f) -> 'a * 'b * 'c * 'd * 'e -> unit -> 'f. Justify your answer.

Déjà vu, anyone?

Strange.

—Grace Jones

Version

Added the commuting diagram in Exercise 0 [13 Feb 2021]

Fixed a second typo in Exercise 19, again thanks to Ann Chen’s eagle eye [09 Feb 2021]

Fixed a typo in Exercise 19, thanks to Ann Chen’s eagle eye [08 Feb 2021]

Added Exercise 17 and its solution [07 Feb 2021]

Created [06 Feb 2021]