OCaml: a language with lexical scope and stuff¶
OCaml is a statically typed language. Its syntactic units are expressions, and evaluating a syntactically correct and type-correct expression yields a value that has the same type as this expression.
Resources¶
- The OCaml code for the present lecture note (latest version: 02 Sep 2022).
Recap¶
So OCaml is a language of algebraic expressions, and these expressions are evaluated in the OCaml toplevel loop, if they are syntactically correct and type correct:
# 1 + 10;;
- : int = 11
# 1 +;;
Characters 3-5:
1 +;;
^^
Error: Syntax error
# 1 + "10";;
Characters 4-8:
1 + "10";;
^^^^
Error: This expression has type string but an expression was expected of type
int
#
It is a language where we can name the result of evaluating an expression (using the let construct), and where we can write our own functions (using the fun construct). For example,
here is a function from integers to integers that squares its argument: fun n -> n * n:
# (fun n -> n * n) 0;; - : int = 0 # (fun n -> n * n) (-1);; - : int = 1 # (fun n -> n * n) 2;; - : int = 4 # (fun n -> n * n) (-3);; - : int = 9 # (fun n -> n * n) 4;; - : int = 16 # (fun n -> n * n) (-5);; - : int = 25 #
here is one way to name this squaring function:
# let square = fun n -> n * n;; val square : int -> int = <fun> # square 6;; - : int = 36 # square (-7);; - : int = 49 #
and here is a more concise way to name this function:
# let square n = n * n;; val square : int -> int = <fun> # square 8;; - : int = 64 # square (-9);; - : int = 81 #
Furthermore functions can take functions as arguments and return functions as results, and this ability lets us write unit-test functions. A unit-test function is used to test another function in predefined cases. For example, here is a unit-test function for a function that maps two integers to the square of their sum. So applying this function to 0 and 0 should return 0, applying this function to 0 and any integer should return the square of this integer, applying this function to any integer and 0 should return the square of this integer, applying this function to 1 and 2 should return 9, etc. All of these cases partially recapitulate in our mind what this function should do, and it is these partial cases that we put into our unit-test function, literally as we are thinking of them, for if we are thinking them, they are worth testing:
let test_squared_sum candidate =
(candidate 0 0 = 0)
&& (candidate 0 1 = 1)
&& (candidate 0 2 = 4)
&& (candidate 1 0 = 1)
&& (candidate 2 0 = 4)
&& (candidate 1 2 = 9)
&& (candidate 2 1 = 9)
&& (candidate 5 5 = 100)
(* etc. *);;
We can then implement squared_sum to our heart’s content:
let squared_sum_v1 i j =
square (i + j);;
let squared_sum_v2 i j =
(i + j) * (i + j);;
let squared_sum_v3 i j =
square i + 2 * i * j + square j;;
let squared_sum_v4 i j =
i * (i + 2 * j) + j * j;;
let squared_sum_v5 i j =
i * i + (2 * i + j) * j;;
(Version 3 is based on the binomial theorem at rank 2, Version 4 factors i on the left in the binomial expansion, and Version 5 factors j on the right in the binomial expansion.)
And then we can check whether they pass the unit test, which they all do:
# test_squared_sum squared_sum_v1;;
- : bool = true
# test_squared_sum squared_sum_v2;;
- : bool = true
# test_squared_sum squared_sum_v3;;
- : bool = true
# test_squared_sum squared_sum_v4;;
- : bool = true
# test_squared_sum squared_sum_v5;;
- : bool = true
#
Turning to Code coverage, the bodies of square and squared_sum do not contain a conditional expression, and therefore these two OCaml functions are exhaustively tested with one application.
Summing up¶
So all in all, OCaml is (a superset of) the language of algebraic expressions from earlier math courses. The unknowns (i.e., the variables such as x, y, etc.) are names that are either
- predeclared (e.g., min_int and max_int),
- declared globally with a let construct, or
- as the formal parameter of a function.
In a functional language, like in mathematics and unlike in imperative programming languages, there is no assignment construct: once declared, variables are immutable. They can be re-declared, but they don’t vary. So we can reason about OCaml expressions the way we reason about algebraic expressions, and the OCaml implementation offers us a way to evaluate these expressions.
Anton: Ah, that’s why functional languages are so popular with students.Alfrothul: How’s that?Anton: No assignments.Alfrothul: No assignments?Anton: Yes. It’s, like, a pun.Halcyon: More like a homonym, no?Anton (conceding Halcyon’s point): Yes. But still a pun.
Declaring several global names at once¶
In OCaml, several (distinct) global names can be defined simultaneously:
- <toplevel-expression> ::= <expression> | let <formal> = <definiens> | let <formal> = <definiens> and ... and <formal> = <definiens>
When let x1 = d1 and x2 = d2 and ... and xN = dN is evaluated in the current environment, and assuming x1, x2, ..., and xN to be all distinct, each of d1, d2, ..., and dN is evaluated in this environment, yielding the values v1, v2, ..., and vN of types t1, t2, ..., tN if these evaluations complete. The subsequent iteration of the toplevel loop takes place with an extended type environment where each xi is bound to the corresponding type ti and an extended value environment where each xi is bound to the corresponding value vi.
In the following interactive session, one name is declared, and then two, and then three. At every iteration of the toplevel loop, for each declared name, the system prints the newly declared name, its type, and the resulting value – or an error message:
For example:
# let a = 1;;
val a : int = 1
# let b = 10 and c = 100;;
val b : int = 10
val c : int = 100
# let d = 1000 and e = 10000 and f = 100000;;
val d : int = 1000
val e : int = 10000
val f : int = 100000
# (a, b, c, d, e);;
- : int * int * int * int * int = (1, 10, 100, 1000, 10000)
#
Attempting to declare the same global name twice gives rise to an error:
# let same = true and same = false;;
Characters 20-24:
let same = true and same = false;;
^^^^
Error: Variable same is bound several times in this matching
#
Since the names are distinct, they cannot shadow each other, and the type environment and the (value) environment can be extended in any order.
Simultaneous declarations make it simple, for example, to (re-)declare each of, e.g., a and f to denote the previous value of the other:
# let a = f and f = a;;
val a : int = 100000
val f : int = 1
# let b = e and c = d and d = c and e = b;;
val b : int = 10000
val c : int = 1000
val d : int = 100
val e : int = 10
# (a, b, c, d, e);;
- : int * int * int * int * int = (100000, 10000, 1000, 100, 10)
#
Interlude about functions¶
Alfrothul: Can we revisit function abstractions and applications?
Mimer: Sure thing.
- <type_environment> ::= . | (<name> : <type>), <type_environment>
- <type> ::= ...
- <expression> ::= ... | <name> | fun <formal> -> <expression> | <expression> <expression>
- <name> ::= a concatenation of characters starting with a lowercase character
- <formal> ::= <name>
| FUN | (x1 : t1), G |- e2 : t2 | |
| G |- fun x1 -> e2 : t1 -> t2 |
| APP | G |- e0 : t1 -> t2 | G |- e1 : t1 | |
| G |- e0 e1 : t2 | |||
Alfrothul: So how are functions applied exactly?
Anton: The previous lecture note said it:
- evaluating fun x1 -> e2 in an environment yields a function; and
- to evaluate e0 e1 in an environment, we first evaluate e0 and
e1 in this environment:
- if either of these first evaluations does not terminate, then evaluating e0 e1 does not terminate;
- if either of these first evaluations raises an error, then evaluating e0 e1 also raises this error; and
- if e0 and e1 evaluate to v0 and v1, then since OCaml is statically typed, v0 denotes a function; evaluating e0 e1 reduces to applying this function to v1.
Alfrothul: Right. But it didn’t say how this function is applied to v1.
Anton: Well, if this function is the negation function or the successor function, which are predefined, this application is an internal matter. What matters to us is that they are applied, and that they return a result.
Alfrothul: Indeed. But if this function is the result of evaluating fun x1 -> e2, for example, then what happens?
Mimer: What happens is that if fun x1 -> e2 was evaluated in the value environment Gv, e2 is evaluated in an extension of Gv where x1 denotes v1.
Dana: Aha, so if v1 represents v1, then e2 is evaluated in (x1 = v1), Gv.
Mimer: Precisely.
Alfrothul: That is consistent with the typing rules. If v1 has type t1, and if the type of fun x1 -> e2 was inferred in the type environment Gt, the type of e2 is inferred in an extension of Gt where x1 denotes t1.
Dana: Right. If t1 represents t1, the type of e2 is inferred in (x1 : t1), Gt.
Mimer: Again, yes.
Dana: I see...
Alfrothul: You see?
Dana: Hum.
Alfrothul: Yes?
Dana: Well, both the type environment and the value environment are extended every time we declare a name at the toplevel.
Alfrothul: Yes.
Dana: But when the value of a function abstraction is applied, its body is evaluated in the environments that were in place when this function abstraction was declared.
Alfrothul: I see what you mean:
# let x = 1;;
val x : int = 1
# let foo = fun y -> x + y;;
val foo : int -> int = <fun>
# foo 10;;
- : int = 11
#
Dana: Right. The denotation of foo is declared in the scope of x.
Pablito: Scope?
Dana: The scope of a name is all the expressions that are evaluated in an environment that binds this name. These expressions occur in the scope of this name.
Pablito: Thanks. I see. So the occurrence of x in the declaration of foo refers to the x that was just declared.
Dana: Yes.
Alfrothul: So what happens if we redeclare x?
Dana: Let’s try:
# let x = "something completely different";;
val x : string = "something completely different"
#
Alfrothul: The type of foo does not change:
# foo;;
- : int -> int = <fun>
#
Dana: Which is good, considering that OCaml is statically typed.
Alfrothul: And if we apply foo, it still behaves as before we redeclared x:
# foo 10;;
- : int = 11
#
Dana: Right – the body of fun y -> x + y is processed in an extension of the environments where x has type int and denotes 1.
Mimer: A property that is named lexical scope: fun y -> x + y was evaluated in a value environment where x was declared, and when the body of fun y -> x + y is evaluated, it is in an extension of this environment, not in an extension of another environment.
Pablito: OK...
Mimer: Stay strong, Pablito, some graphical support for lexical scope comes next.
Bong-sun: Fighting!
Declaring a local name with a local let-expression¶
OCaml also features local let-expressions to declare local names:
- <expression> ::= ... | let <formal> = <definiens> in <expression>
The corresponding typing rule reads as follows, where G stands for <type_environment>, x1 stands for <formal>, e0 and e1 stand for <expression>, and t0 and t1 stand for <type>:
| LET | G |- e1 : t1 | (x1 : t1), G |- e0 : t0 | |
| G |- let x1 = e1 in e0 : t0 | |||
In words,
- in any type environment G, the expression let x1 = e1 in e0 has type t0 whenever (1) in that environment, e1 has type t1 and (2) e0 has type t0 in an extension of this environment where x1 has type t1.
Furthermore,
to evaluate let x1 = e1 in e0 in an environment, we first evaluate e1 in this environment:
if this first evaluation does not terminate, then evaluating let x1 = e1 in e0 does not terminate either;
if this first evaluation raises an error, then evaluating let x1 = e1 in e0 also raises this error;
if e1 evaluates to v1, then evaluating let x1 = e1 in e0 in an environment reduces to evaluating e0 in an extension of this environment where x1 denotes v1;
graphically:

the binding of x1 is local: it vanishes once e0 is evaluated.
Whereas a toplevel let-expression let x = d declares x to be a global name, a let-expression let x = d in e declares x to be local to e.
Vocabulary:
- x, d, and e are often referred to as the formal parameter, the definiens, and the body of let x = d in e, respectively.
Concretely, in the standard global environment (where the addition function is denoted by a name, and this name is implicitly referred to by the infix notation +):
# let x = 1;;
val x : int = 1
# x + 100;;
- : int = 101
# let x = 10 in x + 100;;
- : int = 110
# x;;
- : int = 1
#
In this interaction, and assuming the specialized typing rule for addition from Week 03, ADD, for simplicity,
we declare x globally to denote 1, thereby extending the global environment with one more binding;
we verify that the expression x + 100, which refers to the global name x, evaluates to 101:
LOOKUP_FOUND ----------------------- INT ------------------------- (x : int), G |- x : int (x : int), G |- 100 : int ADD -------------------------------------------------------- (x : int), G |- x + 100 : intwe declare x locally to denote 10, and we verify that the expression x + 100, which refers to the local name x, evaluates to 110;
graphically:

the expression x + 100 is evaluated in an environment where x is bound to 10; this local binding shadows the global binding of x to 1:
LOOKUP_FOUND ---------------------------------- INT ------------------------------------ (x : int), (x : int), G |- x : int (x : int), (x : int), G |- 100 : int ADD ------------------------------------------------------------------------------ (x : int), G |- 10 : int (x : int), (x : int), G |- x + 100 : int LET ------------------------------------------------------------------------ (x : int), G |- let x = 10 in x + 100 : intwe verify that the global name x is unaffected by the previous local declaration:
LOOKUP_FOUND ----------------------- (x : int), G |- x : int
Let-expressions can be nested. This nesting is regulated by lexical scope: the most recently declared name is the one whose binding is in effect.
For example:
# let a = 1 in let b = 10 in a + b;; - : int = 11 #
Graphically:

The expression a + b is evaluated in an environment where b denotes 10, a denotes 1, and the addition function is globally declared:
LOOKUP_FOUND ----------------------- (a : int), G |- a : int LOOKUP_NOT_FOUND_YET ---------------------------------- LOOKUP_FOUND ---------------------------------- (b : int), (a : int), G |- a : int (b : int), (a : int), G |- b : int ADD ------------------------------------------------------------------------------------- (a : int), G |- 10 : int (b : int), (a : int), G |- a + b : int LET --------------------------------------------------------------------------------------- G |- 1 : int (a : int), G |- let b = 10 in a + b : int LET ------------------------------------------------------------- G |- let a = 1 in let b = 10 in a + b : int
When two nested let-expressions declare the same name, the inner binding shadows the outer binding in the extended environment.
For example:
# let a = 1 in let a = 10 in a;; Characters 4-5: let a = 1 in let a = 10 in a;; ^ Warning 26: unused variable a. - : int = 10 #(More about the reason for this gentle warning just below.)
Graphically:

The expression a is evaluated in an environment where a denotes 10 and the addition function is globally declared. The inner binding of a (to 10) shadows its outer binding (to 1), which de facto becomes unused, which the implementation of OCaml gently warned us:
LOOKUP_FOUND --------------------------------- (a : int), G |- 10 : int (a, int), (a : int), G |- a : int LET -------------------------------------------------------------------------- G |- 1 : int (a : int), G |- let a = 10 in a : int LET ---------------------------------------------------------- G |- let a = 1 in let a = 10 in a : intFor another example of nested let-expressions:
# let x = true;; val x : bool = true # let x = 10 in (let x = 1000 in x + 10000) + x;; - : int = 11010 # x;; - : bool = true #
In this interaction,
we (re-)declare x globally to denote true, thereby extending the global environment with one more binding (that shadows the previous bindings of x):
LOOKUP_FOUND -------------------------------------- (x : bool), (x : int), ... |- x : boolwe nest two let-expressions;
graphically:

the expression x + 10000 is evaluated in an environment where x is bound to 1000; this local binding shadows the outer bindings (both the local one to 10 and the global one to true);
the expression ... + x is evaluated in an environment where x is bound to 10; this local binding shadows the outer, global one to true:
LOOKUP_FOUND ---------------------------------------------- INT -------------------------------------------------- (x : int), (x : int), (x : bool), G |- x : int (x : int), (x : int), (x : bool), G |- 10000 : int INT -------------------------------------- ADD -------------------------------------------------------------------------------------------------------- (x : int), (x : bool), G |- 1000 : int (x : int), (x : int), (x : bool), G |- x + 10000 : int LET ------------------------------------------------------------------------------------------------------------- LOOKUP_FOUND ----------------------------------- (x : int), (x : bool), G |- let x = 1000 in x + 10000 : int (x : int), (x : bool), G |- x : int ADD ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- (x : bool), G |- 10 : int (x : int), (x : bool), G |- (let x = 1000 in x + 10000) + x : int LET -------------------------------------------------------------------------------------------------- (x : bool), G |- let x = 10 in (let x = 1000 in x + 10000) + x : int
we verify that the global name x is unaffected by the previous nested local declarations:
LOOKUP_FOUND ------------------------- (x : bool), G |- x : bool
We can also name functions locally:
# let identity = fun x -> x
in (identity 1) + (identity 10);;
- : int = 11
# (let x = fun x -> x + 1 in x 10) + (let x = fun x -> x + 100 in x 1000);;
- : int = 1111
#
Food for thought:
Here is a graphical rendition of the first interaction:

Make sure you understand why the result is 11.
Here is a graphical rendition of the second interaction:

Make sure you understand why the result is 1111.
Here is the same scenario with the more concise way of declaring functions:
# let identity x = x in (identity 1) + (identity 10);; - : int = 11 # (let x x = x + 1 in x 10) + (let x x = x + 100 in x 1000);; - : int = 1111 #
The overloading of x makes the last expression unnecessarily hard to read. In practice, better use different names and write:
# (let f x = x + 1 in f 10) + (let g y = y + 100 in g 1000);; - : int = 1111 #
Juliet (heartbreakingly): What’s in a name?Halcyon: Aww...
Another example of shadowing¶
Anton: What if we shadowed a name that has one type with a name that has another type?
Alfrothul: Well, it should work.
Pablito: Er... An example, perhaps?
Anton: How about something like this:
fun x n -> (let x = n in x > 0) || x
Alfrothul: OK, so since || is logical disjunction, x must have type bool.
Dana: And since n is aliased to x and then x is compared to 0, n must have type int.
Anton: Right. So all it all, it should have type, well, bool -> int -> bool, right?
Pablito (fast on his feet): Let’s ask OCaml:
# fun x n -> (let x = n in x > 0) || x;;
- : bool -> int -> bool = <fun>
#
Alfrothul: Yup, that does it.
Halcyon: But what does this OCaml function do?
Dana (kindly): That doesn’t really matter. The point is that we now have an inner occurrence of x that shadows the outer one and has another type.
Halcyon: Ah, OK.
Alfrothul: The question is how OCaml comes up with this type.
Anton: And to answer this question, let’s construct the proof tree. Here is its root and two typing rules for disjunction and comparison:
. |- fun x n -> (let x = n in x > 0) || x : bool -> int -> bool
| DISJ | G |- e1 : bool | G |- e2 : bool | |
| G |- e1 || e2 : bool | |||
| GREATER | G |- e1 : int | G |- e2 : int | |
| G |- e1 > e2 : bool | |||
Alfrothul: Either that, or bind the names of these operators in the given environment:
((||) : bool -> bool -> bool), ((>) : int -> int -> bool), . |- fun x n -> (let x = n in x > 0) || x : bool -> int -> bool
Anton: Right, and then using the APP rule. Let’s go with the two extra rules.
Alfrothul: Sure. Anyway, fun x n -> ... is syntactic sugar for fun x -> fun n -> ..., so let’s apply the FUN rule twice:
(n : int), (x : bool), . |- (let x = n in x > 0) || x : bool
FUN -----------------------------------------------------------------
(x : bool), . |- fun n -> (let x = n in x > 0) || x : int -> bool
FUN ----------------------------------------------------------------------
. |- fun x -> fun n -> (let x = n in x > 0) || x : bool -> int -> bool
Anton: And now for the DISJ rule, where G is instantiated with (n : int), (x : bool), ., e1 is instantiated with let x = n in x > 0, and e2 is instantiated with x:
(n : int), (x : bool), . |- let x = n in x > 0 : bool (n : int), (x : bool), . |- x : bool
DISJ ---------------------------------------------------------------------------------------------
(n : int), (x : bool), . |- (let x = n in x > 0) || x : bool
FUN -----------------------------------------------------------------
(x : bool), . |- fun n -> (let x = n in x > 0) || x : int -> bool
FUN ----------------------------------------------------------------------
. |- fun x -> fun n -> (let x = n in x > 0) || x : bool -> int -> bool
Alfrothul: OK, this is where the action is. We apply the LET rule on the left subtree, where G is instantiated with (n : int), (x : bool), ., x1 is instantiated with x, e1 is instantiated with n, t1 is instantiated with int, e2 is instantiated with x > 0, and t2 is instantiated with bool:
(n : int), (x : bool), . |- n : int (x : int), (n : int), (x : bool), . |- x > 0 : bool
LET ------------------------------------------------------------------------------------------
(n : int), (x : bool), . |- let x = n in x > 0 : bool (n : int), (x : bool), . |- x : bool
DISJ ----------------------------------------------------------------------------------------------------------------------------------
(n : int), (x : bool), . |- (let x = n in x > 0) || x : bool
FUN -----------------------------------------------------------------
(x : bool), . |- fun n -> (let x = n in x > 0) || x : int -> bool
FUN ----------------------------------------------------------------------
. |- fun x -> fun n -> (let x = n in x > 0) || x : bool -> int -> bool
Anton: The left subtree begs one to apply LOOKUP_FOUND:
LOOKUP_FOUND -----------------------------------
(n : int), (x : bool), . |- n : int (x : int), (n : int), (x : bool), . |- x > 0 : bool
LET ------------------------------------------------------------------------------------------
(n : int), (x : bool), . |- let x = n in x > 0 : bool (n : int), (x : bool), . |- x : bool
DISJ ----------------------------------------------------------------------------------------------------------------------------------
(n : int), (x : bool), . |- (let x = n in x > 0) || x : bool
FUN -----------------------------------------------------------------
(x : bool), . |- fun n -> (let x = n in x > 0) || x : int -> bool
FUN ----------------------------------------------------------------------
. |- fun x -> fun n -> (let x = n in x > 0) || x : bool -> int -> bool
Alfrothul: Next step, the comparison, for which we apply the GREATER rule:
(x : int), (n : int), (x : bool), . |- x : int (x : int), (n : int), (x : bool), . |- 0 : int
LOOKUP_FOUND ----------------------------------- GREATER ------------------------------------------------------------------------------------------------
(n : int), (x : bool), . |- n : int (x : int), (n : int), (x : bool), . |- x > 0 : bool
LET --------------------------------------------------------------------------------------------------
(n : int), (x : bool), . |- let x = n in x > 0 : bool (n : int), (x : bool), . |- x : bool
DISJ ---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
(n : int), (x : bool), . |- (let x = n in x > 0) || x : bool
FUN -----------------------------------------------------------------
(x : bool), . |- fun n -> (let x = n in x > 0) || x : int -> bool
FUN ----------------------------------------------------------------------
. |- fun x -> fun n -> (let x = n in x > 0) || x : bool -> int -> bool
Anton: And now we can simply apply the LOOKUP_FOUND rule and the INT rule for the left subtree of the disjunction to be complete:
LOOKUP_FOUND ---------------------------------------------- INT ----------------------------------------------
(x : int), (n : int), (x : bool), . |- x : int (x : int), (n : int), (x : bool), . |- 0 : int
LOOKUP_FOUND ----------------------------------- GREATER ----------------------------------------------------------------------------------------------------
(n : int), (x : bool), . |- n : int (x : int), (n : int), (x : bool), . |- x > 0 : bool
LET -------------------------------------------------------------------------------------------------------
(n : int), (x : bool), . |- let x = n in x > 0 : bool (n : int), (x : bool), . |- x : bool
DISJ ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
(n : int), (x : bool), . |- (let x = n in x > 0) || x : bool
FUN -----------------------------------------------------------------
(x : bool), . |- fun n -> (let x = n in x > 0) || x : int -> bool
FUN ----------------------------------------------------------------------
. |- fun x -> fun n -> (let x = n in x > 0) || x : bool -> int -> bool
Pablito: As for the right subtree of the disjunction, we need to apply LOOKUP_NOT_FOUND_YET and then LOOKUP_FOUND to complete it:
LOOKUP_FOUND ---------------------------------------------- INT ----------------------------------------------
(x : int), (n : int), (x : bool), . |- x : int (x : int), (n : int), (x : bool), . |- 0 : int
LOOKUP_FOUND ----------------------------------- GREATER ---------------------------------------------------------------------------------------------------- LOOKUP_FOUND -------------------------
(n : int), (x : bool), . |- n : int (x : int), (n : int), (x : bool), . |- x > 0 : bool (x : bool), . |- x : bool
LET ------------------------------------------------------------------------------------------------------- LOOKUP_NOT_FOUND_YET ------------------------------------
(n : int), (x : bool), . |- let x = n in x > 0 : bool (n : int), (x : bool), . |- x : bool
DISJ ---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
(n : int), (x : bool), . |- (let x = n in x > 0) || x : bool
FUN -----------------------------------------------------------------
(x : bool), . |- fun n -> (let x = n in x > 0) || x : int -> bool
FUN ----------------------------------------------------------------------
. |- fun x -> fun n -> (let x = n in x > 0) || x : bool -> int -> bool
Anton: And now the proof tree is complete.
Alfrothul: It’s kind of a downer, isn’t it?
Anton: You mean there is nothing new here?
Alfrothul: Right. We just applied the rules, and once the environment was extended with a new binding for x, that was it, the previous occurrence of x was shadowed.
Dana: Guys, the glass is also half full – if you can use what you already know to explain something new, it’s evidence that what you know is useful.
Mimer: Correct. It also means that not everything new is novel. It would be unsettling to always need new things to explain new things, wouldn’t it?
Loki: Self-reference and Aristotle in the same sentence, Mimer. You’re doing good!
Dana (unfazed): So, Mimer, you prefer the other root, don’t you:
((||) : bool -> bool -> bool), ((>) : int -> int -> bool), . |- fun x n -> (let x = n in x > 0) || x : bool -> int -> bool
Pablito: Ah, right, because then we use the APP rule twice, instead of needing two new rules.
Mimer: Yup.
Loki (indefatigable): Well, you have to use the APP rule four times, instead of each DISJ and GREATER once, so there is that too.
Anton: True, but that is because one is general, and the two others are specialized.
Halcyon (coughing in his hand): S-m-n.
Alfrothul: Wait. I guess we could derive the two other in terms of APP, couldn’t we?
Anton: Let’s try. Here is the root:
(b2 : bool), (b1 : bool), . |- b1 || b2 : bool
Alfrothul: Well, actually, (||) is a name, so here is the root:
(b2 : bool), (b1 : bool), ((||) : bool -> bool -> bool). |- (||) b1 b2 : bool
Pablito (jumping in): Ah, right, we should apply the APP rule:
(b2 : bool), (b1 : bool), ((||) : bool -> bool -> bool). |- (||) b1 : bool -> bool (b2 : bool), (b1 : bool), ((||) : bool -> bool -> bool). |- b2 : bool
APP -----------------------------------------------------------------------------------------------------------------------------------------------------------
(b2 : bool), (b1 : bool), ((||) : bool -> bool -> bool). |- (||) b1 b2 : bool
Anton: Right. And we can take care of the right subtree straight off, using the LOOKUP_FOUND rule:
LOOKUP_FOUND ---------------------------------------------------------------------
(b2 : bool), (b1 : bool), ((||) : bool -> bool -> bool). |- (||) b1 : bool -> bool (b2 : bool), (b1 : bool), ((||) : bool -> bool -> bool). |- b2 : bool
APP ------------------------------------------------------------------------------------------------------------------------------------------------------------------------
(b2 : bool), (b1 : bool), ((||) : bool -> bool -> bool). |- (||) b1 b2 : bool
Pablito: For the left subtree, we should apply the APP rule again:
(b2 : bool), (b1 : bool), ((||) : bool -> bool -> bool). |- (||) : bool -> bool -> bool (b2 : bool), (b1 : bool), ((||) : bool -> bool -> bool). |- b1 : bool
APP ---------------------------------------------------------------------------------------------------------------------------------------------------------------- LOOKUP_FOUND ---------------------------------------------------------------------
(b2 : bool), (b1 : bool), ((||) : bool -> bool -> bool). |- (||) b1 : bool -> bool (b2 : bool), (b1 : bool), ((||) : bool -> bool -> bool). |- b2 : bool
APP ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
(b2 : bool), (b1 : bool), ((||) : bool -> bool -> bool). |- (||) b1 b2 : bool
Alfrothul: Now we just need to apply LOOKUP_NOT_FOUND_YET and LOOKUP_FOUND, and we are done.
Dana: So yes, DISJ and GREATER are derived rules, and yes, for each of them, we need to apply APP twice.
Mimer: It’s a trade-off.
Exercise 09¶
Consider the following series of definitions:
let g = 1;; let foo h = g + h;; let g = true;;
What does if g then foo 10 else 11 evaluate to? To an integer or is there a type error? Why is that?
Consider the following expression:
let g = 1 in let foo h = g + h in let g = true in if g then foo 10 else 11;;What does this expression evaluate to? To an integer or is there a type error? Why is that?
Consider the following expression:
let x = 1 in let foo y = x + y in let x = 100 in if true then foo 10 else x;;What does this expression evaluate to? To 11 or to 110? Why is that?
Food for thought about Exercise 09¶
The toplevel loop constructs increasingly nested scopes. For example, let G_init denote OCaml’s initial value environment. The first declaration expands this environment:
OCaml version 4.01.0
# let a = 1;;
val a : int = 1
#
Graphically:
G_init
+------------
| a : int = 1
|
The second declaration expands this expanded environment:
# let b = 10 and c = 100;;
val b : int = 10
val c : int = 100
#
Graphically:
G_init
+------------
| a : int = 1
| +--------------
| | b : int = 10
| | c : int = 100
| |
The third declaration further expands this expanded environment:
# let d = 1000 and e = 10000 and f = 100000;;
val d : int = 1000
val e : int = 10000
val f : int = 100000
#
Graphically:
G_init
+------------
| a : int = 1
| +--------------
| | b : int = 10
| | c : int = 100
| | + --------------------
| | | val d : int = 1000
| | | val e : int = 10000
| | | val f : int = 100000
| | |
Likewise for the fourth declaration:
# let a = f and f = a;;
val a : int = 100000
val f : int = 1
#
Graphically:
G_init
+------------
| a : int = 1
| +--------------
| | b : int = 10
| | c : int = 100
| | +---------------------
| | | val d : int = 1000
| | | val e : int = 10000
| | | val f : int = 100000
| | | +------------------------
| | | | val a : int = 100000
| | | | val f : int = 1
| | | |
And so on, until the end of this OCaml interactive session.
Declaring several names with a local let-expression¶
In OCaml, several (distinct) local names can be defined simultaneously:
- <expression> ::= ... | let <formal> = <definiens> in <expression> | let <formal> = <definiens> and ... and <formal> = <definiens> in <expression>
When let x1 = d1 and x2 = d2 and ... and xN = dN in e is evaluated in an environment, and assuming x1, x2, ..., and xN to be all distinct, each of d1, d2, ..., and dN is evaluated in this environment, yielding the values v1, v2, ..., and vN of types t1, t2, ..., tN if these evaluations complete. The body, i.e., e is then evaluated in an environment where x1, x2, ..., and xN respectively denote v1, v2, ..., and vN, yielding a value w if this evaluation completes. The result of evaluating the let expression is w. The bindings of the formals are local: they vanish once the let-expression is evaluated.
The corresponding typing rule reads as follows, where G stands for <type_environment>, x1, ..., and xN stand for <formal> and are all distinct, e0, e1, ..., and eN stand for <expression>, and t0, t1, ..., and tN stand for <type>:
| LET+ | G |- e1 : t1 | ... | G |- eN : tN | (x1 : t1), ..., (xN : tN), G |- e0 : t0 | |
| G |- let x1 = e1 and ... and xN = eN in e0 : t0 | |||||
In words,
- in any type environment G, the expression let x1 = e1 and ... xN = eN in e0 has type t0 whenever (1) in that environment, e1 has type t1, e2 has type t2, ..., and eN has type tN, and (2) e0 has type t0 in an extension of this environment where x1 has type t1, x2 has type t2, ..., and xN has type tN.
Furthermore,
to evaluate let x1 = e1 and ... xN = eN in e0 in the current environment, we first evaluate the definienses, i.e., e1, ..., and eN in this current environment:
if either of these first evaluations does not terminate, then evaluating let x1 = e1 and ... xN = eN in e0 does not terminate;
if either of these first evaluations raises an error, then evaluating let x1 = e1 and ... xN = eN in e0 also raises this error;
if e1, ..., and eN in the current environment respectively evaluate to v1, ... and vN, then evaluating let x1 = e1 and ... xN = eN in e0 in the current environment reduces to evaluating e0 in an extended environment where x1 denotes v1, ..., and xN denotes vN;
the bindings of x1, ..., and xN are local: they vanish once e0 is evaluated;
Let us review each of these points.
For example:
# let x = 1;; val x : int = 1 # let x = 10 and y = 100 in x + y;; - : int = 110 # x;; - : int = 1 # y;; Characters 0-1: y;; ^ Error: Unbound value y #
Graphically:

Naturally, let-expressions that declare several names can be nested:
# let a = 1 and b = 10 and c = 100 in let c = b in a + b + c;; Characters 25-26: let a = 1 and b = 10 and c = 100 in let c = b in a + b + c;; ^ Warning 26: unused variable c. - : int = 21 #The result is 21 because the inner declaration of c binds it to the denotation of b, which is 10. The inner binding of c (to 10) shadows its outer binding (to 100), which de facto becomes unused, which the implementation of OCaml gently tells us with a warning.
Graphically:

The expression a + b + c is evaluated in an environment where c denotes 10, b denotes 10, a denotes 1, and the addition function is globally declared. (The outer binding of c to 100 is shadowed.)
In the previous example, even if b is re-declared in the scope of c, the denotation of c is unaffected:
# let a = 1 and b = 10 and c = 100 in let c = b in let b = 1000 in a + b + c;; Characters 25-26: let a = 1 and b = 10 and c = 100 in let c = b in let b = 1000 in a + b + c;; ^ Warning 26: unused variable c. - : int = 1011 #Graphically:

The expression a + b + c is evaluated in an environment where b denotes 1000, c denotes 10, a denotes 1, and the addition function is globally declared. (The outer bindings of c to 100 and of b to 10 are shadowed.)
Each of the definienses is independent of the others and of the formals. In the following example, we put this independence to use:
# let x = 10 and y = 100 in let x = y and y = x in y - x;; - : int = -90 #
Graphically:

Environment extensions co-exist without interference. For example:
# let x = 10 in (let y = 100 in x + y) + (let y = 1000 in x + y);; - : int = 1120 #
Graphically:
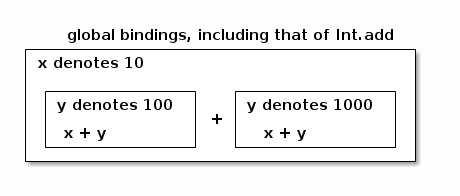
- The first occurrence of x + y is evaluated in an environment where y denotes 100, x denotes 10, and the addition function is globally declared.
- The second occurrence of x + y is evaluated in an environment where y denotes 1000, x denotes 10, and the addition function is globally declared.
Note: the order in the boxes does not matter, what matters is their nesting. For example, the boxes above can be drawn just as well as follows:

Likewise, the OCaml expression could also have been variously written as follows:
let x = 10 in (let y = 100 in x + y) + (let y = 1000 in x + y);; let x = 10 in (let y = 100 in x + y) + (let y = 1000 in x + y);; let x = 10 in (let y = 100 in x + y) + (let y = 1000 in x + y);;One should write and draw whatever is simplest and most readable.
Finally, shadowed bindings in lexical scope and non-interfering co-existence of environment extensions combine harmoniously. So for example, an expression such as:
let x = 1 in (let y = 10 in let x = 100 in x + y) + x + (let y = 1000 in let y = 10000 in x + y);;
evaluates to 10112.
Graphically:
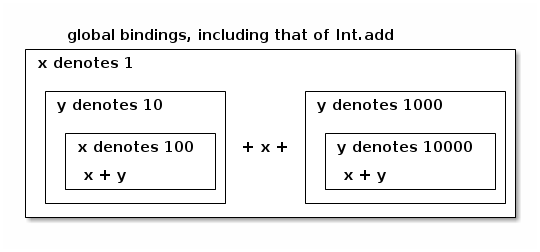
- The first occurrence of x + y, on the left, is evaluated in an environment where x denotes 100, y denotes 10, and the addition function is globally declared. (The outer binding of x to 1 is shadowed.)
- The expression x, in the middle, is evaluated in an environment where x denotes 1 and the addition function is globally declared.
- The second occurrence of x + y, on the right, is evaluated in an environment where y denotes 10000, x denotes 1, and the addition function is globally declared. (The outer binding of y to 1000 is shadowed.)
Pairs, revisited¶
Two values can be grouped into a pair of values:
Introduction:
A pair is constructed by grouping its components between parentheses and separating them with a comma:
# (1, 10);; - : int * int = (1, 10) #
Pairs can be nested:
# (1, (10, 100));; - : int * (int * int) = (1, (10, 100)) # ((1, 10), 100);; - : (int * int) * int = ((1, 10), 100) #
Elimination:
A pair is deconstructed (or again: destructured) using a mild notational extension of the formals in a let-expression:
# let (a, b) = (1, 10) in a + b;; - : int = 11 # let p = (1, 10);; val p : int * int = (1, 10) # let (a, b) = p in a + b;; - : int = 11 # let (a, (b, c)) = (1, (10, 100)) in a + b + c;; - : int = 111 # let ((a, b), c) = ((1, 10), 100) in a + b + c;; - : int = 111 #
This notational extension scales to the formals in functions:
# (fun (a, b) -> a + b) (1, 10);; - : int = 11 # let plus (a, b) = a + b;; val plus : int * int -> int = <fun> # plus (1, 10);; - : int = 11 #
So formals can reflect the structure of the domain of a function:
# (fun (a, (b, c)) -> a + b + c) (1, (10, 100));; - : int = 111 # (fun ((a, b), c) -> a + b + c) ((1, 10), 100);; - : int = 111 #
For example, the following function maps pairs of integers and Booleans to pairs of Booleans and integers:
# let swap_pair_of_int_and_bool (i, b) = (not b, i + 1);; val swap_pair_of_int_and_bool : int * bool -> bool * int = <fun> #
Tuples, revisited¶
Any number (greater than 2) of values can be grouped into a tuple of values:
Introduction:
A tuple is constructed by grouping its components between parentheses and separating them with a comma:
# (1, 10, 100);; - : int * int * int = (1, 10, 100) # (1, 10, 100, 1000);; - : int * int * int * int = (1, 10, 100, 1000) #
Tuples can be nested:
# ((1, 10), (2, 20, 200));; - : (int * int) * (int * int * int) = ((1, 10), (2, 20, 200)) # ((1, 10), (2, 20, 200), (3, 30, 300, 3000));; - : (int * int) * (int * int * int) * (int * int * int * int) = ((1, 10), (2, 20, 200), (3, 30, 300, 3000)) #
Elimination:
A tuple is deconstructed (or again: destructured) using a similar notational extension of the formals in a let-expression:
# let (a, b, c) = (1, 10, 100) in a + b + c;; - : int = 111 # let t3 = (1, 10, 100);; val t3 : int * int * int = (1, 10, 100) # let (a, b, c) = t3 in a + b + c;; - : int = 111 # let (a, b, c, d) = (1, 10, 100, 1000) in a + b + c + d;; - : int = 1111 # let t4 = (1, 10, 100, 1000);; val t4 : int * int * int * int = (1, 10, 100, 1000) # let (a, b, c, d) = t4 in a + b + c + d;; - : int = 1111 #
Again, this notational extension scales to the formals in functions:
# let foo (a, b, c, d) = a + b + c + d;; val foo : int * int * int * int -> int = <fun> # foo t4;; - : int = 1111 #
The empty tuple, revisited¶
The empty tuple has the singleton type unit:
# ();;
- : unit = ()
#
(“Singleton” because there is only one value of that type.)
Both let-expressions and functions admit an empty tuple as formal:
# let the_empty_tuple = ();;
val the_empty_tuple : unit = ()
# let () = the_empty_tuple in 42;;
- : int = 42
# let the_ultimate_answer = fun () -> 42;;
val the_ultimate_answer : unit -> int = <fun>
# the_ultimate_answer the_empty_tuple;;
- : int = 42
# let the_ultimate_answer' () = 42;;
val the_ultimate_answer' : unit -> int = <fun>
# the_ultimate_answer' the_empty_tuple;;
- : int = 42
#
Formals, formally¶
The mild notational extension of the formals in lambda-abstractions and in let expressions is accounted for by the following refined BNF:
In this grouping, all the names must be distinct.
For example, this extension provides an alternative to declaring several global names at once using a single declaration instead of a double one:
# let x = 10 and y = 100;;
val x : int = 10
val y : int = 100
# let (x, y) = (10, 100);;
val x : int = 10
val y : int = 100
#
Likewise for (re-)declaring each of x and y to denote the previous value of the other:
# let x = y and y = x;;
val x : int = 100
val y : int = 10
# let (x, y) = (y, x);;
val x : int = 10
val y : int = 100
#
As for _, it is used as placeholder for a formal parameter that is unused. So for example, the constant function that returns 42 can be equivalently written as fun x -> 42 or as fun _ -> 42.
As seen earlier, OCaml gently warns us about unused formal parameters in let expressions:
# let a = 1 in let a = 10 in a;;
Characters 4-5:
let a = 1 in let a = 10 in a;;
^
Warning 26: unused variable a.
- : int = 10
#
This warning is lifted by replacing the unused formal with _:
# let _ = 1 in let a = 10 in a;;
- : int = 10
#
It is considered good style to not have warnings.
Interlude¶
Alfrothul: Neat extension.
Anton: Right. It makes it possible to implement a swap function really concisely:
# fun (a, b) -> (b, a);;
- : 'a * 'b -> 'b * 'a = <fun>
#
Alfrothul: And projections too.
Anton (o_o): Projections.
Alfrothul: Well, yes – given a pair, return one of its first components:
# let fst (a, _) = a;;
val fst : 'a * 'b -> 'a = <fun>
#
Anton: The first projection of a pair, I see. And likewise for the second projection:
# let snd (_, b) = b;;
val snd : 'a * 'b -> 'b = <fun>
#
Alfrothul: Yup.
Pablito: But how do we write the corresponding proof tree? The FUN rule and the LET rule are stated for names, not for groupings of names.
Mimer: Well spotted, Pablito. These two rules need to be adapted to account for the mild extension of formals.
Loki: The extension doesn’t look mild.
Mimer: But it is essentially simple, since the extension is syntactic sugar. For example, look at Anton’s swap function:
(a : 'a), (b : 'b), . |- (b, a) : 'b * 'a
FUN ----------------------------------------------
. |- fun (a, b) -> (b, a) : 'a * 'b -> 'b * 'a
Loki: Shouldn’t it be:
(b : 'b), (a : 'a), . |- (b, a) : 'b * 'a
FUN ----------------------------------------------
. |- fun (a, b) -> (b, a) : 'a * 'b -> 'b * 'a
Mimer: It doesn’t matter because all the names in a grouping are distinct.
Alfrothul: I see. And then we don’t extend the environment for the placeholder:
LOOKUP_FOUND ---------------------
(a : 'a), . |- a : 'a
FUN ------------------------------------
. |- fun (a, _) -> a : 'a * 'b -> 'a
Pablito: Goodbye, LOOKUP_NOT_FOUND_YET.
Dana: Not just that – we can also program functions that curry and uncurry other functions.
Anton (o_o): Curry and uncurry.
Mimer: The names come after Haskell Curry, and are due to Christopher Strachey.
Dana: An uncurried function of arity 2 has type 'a * 'b -> 'c whereas the corresponding curried function has type 'a -> 'b -> 'c.
Alfrothul: So you mean that the curry function has type ('a * 'b -> 'c) -> 'a -> 'b -> 'c?
Anton: And that the uncurry function has type ('a -> 'b -> 'c) -> 'a * 'b -> 'c?
Dana: Yes I do.
Pablito: I think I know how to construct the corresponding OCaml function.
Halcyon: You do?
Pablito: I think so, yes. We just need to construct a proof tree. Here is its root, writing ? to stand for the expression we are looking for:
G |- ? : ('a * 'b -> 'c) -> 'a -> 'b -> 'c
Alfrothul: Right. Since the type is that of a function, we have no other choice but using the FUN rule, which forces ? to be fun ... -> .... Since the type in the domain of this function is that of a function, let us name the corresponding formal parameter something intuitive, like, f, and write ?? to stand for the sub-expression we are looking for:
(f : 'a * 'b -> 'c), G |- ?? : 'a -> 'b -> 'c
FUN ----------------------------------------------------
G |- fun f -> ?? : ('a * 'b -> 'c) -> 'a -> 'b -> 'c
Anton: Well, since 'a -> 'b -> 'c is the type of a function, we have no other choice but using the FUN rule, which forces ?? to be fun ... -> ....
Pablito (judiciously): Actually, we have no other choice but using the FUN rule twice in a row, since the codomain of 'a -> 'b -> 'c is 'b -> 'c, i.e., the type of another function. So ?? is forced to be fun ... -> fun ... -> ....
Halcyon: Can I choose the name of the two formal parameters?
Dana: Pray do.
Halcyon: How about a and b? We could also write ??? to stand for the sub-expression we are looking for.
Pablito: That’s pretty intuitive indeed. All in all, fun a -> fun b -> ??? replaces ??:
(f : 'a * 'b -> 'c), G |- fun a -> fun b -> ??? : 'a -> 'b -> 'c
FUN -----------------------------------------------------------------------
G |- fun f -> fun a -> fun b -> ??? : ('a * 'b -> 'c) -> 'a -> 'b -> 'c
Halcyon: Thank you.
Pablito: So let’s use the FUN rule twice in a row:
(b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- ??? : 'c
FUN -----------------------------------------------------------
(a : 'a), (f : 'a * 'b -> 'c), G |- fun b -> ??? : 'b -> 'c
FUN ----------------------------------------------------------------
(f : 'a * 'b -> 'c), G |- fun a -> fun b -> ??? : 'a -> 'b -> 'c
FUN -----------------------------------------------------------------------
G |- fun f -> fun a -> fun b -> ??? : ('a * 'b -> 'c) -> 'a -> 'b -> 'c
Anton: Now we need to conjure up an expression of type 'c in the stead of ???.
Alfrothul: We need to apply f to something – which we can write ???? – so let’s replace ??? by f ???? and use the APP rule:
(b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- f : 'a * 'b -> 'c (b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- ???? : 'a * 'b
APP -------------------------------------------------------------------------------------------------------------------------------
(b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- f ???? : 'c
FUN --------------------------------------------------------------
(a : 'a), (f : 'a * 'b -> 'c), G |- fun b -> f ???? : 'b -> 'c
FUN -------------------------------------------------------------------
(f : 'a * 'b -> 'c), G |- fun a -> fun b -> f ???? : 'a -> 'b -> 'c
FUN --------------------------------------------------------------------------
G |- fun f -> fun a -> fun b -> f ???? : ('a * 'b -> 'c) -> 'a -> 'b -> 'c
Pablito: The left branch is easy to build:
LOOKUP_FOUND -------------------------------------------
(f : 'a * 'b -> 'c), G |- f : 'a * 'b -> 'c
LOOKUP_NOT_FOUND_YET -----------------------------------------------------
(a : 'a), (f : 'a * 'b -> 'c), G |- f : 'a * 'b -> 'c
LOOKUP_NOT_FOUND_YET ---------------------------------------------------------------
(b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- f : 'a * 'b -> 'c (b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- ???? : 'a * 'b
APP -------------------------------------------------------------------------------------------------------------------------------
(b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- f ???? : 'c
FUN --------------------------------------------------------------
(a : 'a), (f : 'a * 'b -> 'c), G |- fun b -> f ???? : 'b -> 'c
FUN -------------------------------------------------------------------
(f : 'a * 'b -> 'c), G |- fun a -> fun b -> f ???? : 'a -> 'b -> 'c
FUN --------------------------------------------------------------------------
G |- fun f -> fun a -> fun b -> f ???? : ('a * 'b -> 'c) -> 'a -> 'b -> 'c
Anton: As for ????, it has the type of a pair, so we need a pair constructor. Let’s write (?????, ??????) in the stead of ????:
LOOKUP_FOUND -------------------------------------------
(f : 'a * 'b -> 'c), G |- f : 'a * 'b -> 'c
LOOKUP_NOT_FOUND_YET -----------------------------------------------------
(a : 'a), (f : 'a * 'b -> 'c), G |- f : 'a * 'b -> 'c
LOOKUP_NOT_FOUND_YET ---------------------------------------------------------------
(b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- f : 'a * 'b -> 'c (b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- (?????, ??????) : 'a * 'b
APP -------------------------------------------------------------------------------------------------------------------------------------------
(b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- f (?????, ??????) : 'c
FUN -------------------------------------------------------------------------
(a : 'a), (f : 'a * 'b -> 'c), G |- fun b -> f (?????, ??????) : 'b -> 'c
FUN ------------------------------------------------------------------------------
(f : 'a * 'b -> 'c), G |- fun a -> fun b -> f (?????, ??????) : 'a -> 'b -> 'c
FUN -------------------------------------------------------------------------------------
G |- fun f -> fun a -> fun b -> f (?????, ??????) : ('a * 'b -> 'c) -> 'a -> 'b -> 'c
Alfrothul: Well, we have no other choice but using the PAIR rule:
LOOKUP_FOUND -------------------------------------------
(f : 'a * 'b -> 'c), G |- f : 'a * 'b -> 'c
LOOKUP_NOT_FOUND_YET -----------------------------------------------------
(a : 'a), (f : 'a * 'b -> 'c), G |- f : 'a * 'b -> 'c (b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- ????? : 'a (b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- ?????? : 'b
LOOKUP_NOT_FOUND_YET --------------------------------------------------------------- PAIR ---------------------------------------------------------------------------------------------------------------------
(b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- f : 'a * 'b -> 'c (b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- (?????, ??????) : 'a * 'b
APP -----------------------------------------------------------------------------------------------------------------------------------------------
(b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- f (?????, ??????) : 'c
FUN -------------------------------------------------------------------------
(a : 'a), (f : 'a * 'b -> 'c), G |- fun b -> f (?????, ??????) : 'b -> 'c
FUN ------------------------------------------------------------------------------
(f : 'a * 'b -> 'c), G |- fun a -> fun b -> f (?????, ??????) : 'a -> 'b -> 'c
FUN -------------------------------------------------------------------------------------
G |- fun f -> fun a -> fun b -> f (?????, ??????) : ('a * 'b -> 'c) -> 'a -> 'b -> 'c
Alfrothul: So we need something of type 'a and something of type 'b.
Pablito: According to the type environment, a and b fit the bill, so let’s replace ????? with a and ?????? with b:
LOOKUP_FOUND -------------------------------------------
(f : 'a * 'b -> 'c), G |- f : 'a * 'b -> 'c
LOOKUP_NOT_FOUND_YET -----------------------------------------------------
(a : 'a), (f : 'a * 'b -> 'c), G |- f : 'a * 'b -> 'c (b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- a : 'a (b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- b : 'b
LOOKUP_NOT_FOUND_YET --------------------------------------------------------------- PAIR ------------------------------------------------------------------------------------------------------------
(b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- f : 'a * 'b -> 'c (b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- (a, b) : 'a * 'b
APP --------------------------------------------------------------------------------------------------------------------------------------
(b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- f (a, b) : 'c
FUN ----------------------------------------------------------------
(a : 'a), (f : 'a * 'b -> 'c), G |- fun b -> f (a, b) : 'b -> 'c
FUN ---------------------------------------------------------------------
(f : 'a * 'b -> 'c), G |- fun a -> fun b -> f (a, b) : 'a -> 'b -> 'c
FUN ----------------------------------------------------------------------------
G |- fun f -> fun a -> fun b -> f (a, b) : ('a * 'b -> 'c) -> 'a -> 'b -> 'c
Anton: And now we only need to use LOOKUP_NOT_FOUND_YET and LOOKUP_FOUND to complete the proof tree:
LOOKUP_FOUND ------------------------------------------- LOOKUP_FOUND ------------------------------------------
(f : 'a * 'b -> 'c), G |- f : 'a * 'b -> 'c (a : 'a), (f : 'a * 'b -> 'c), G |- a : 'a
LOOKUP_NOT_FOUND_YET ----------------------------------------------------- LOOKUP_NOT_FOUND_YET ---------------------------------------------------- LOOKUP_FOUND ----------------------------------------------------
(a : 'a), (f : 'a * 'b -> 'c), G |- f : 'a * 'b -> 'c (b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- a : 'a (b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- b : 'b
LOOKUP_NOT_FOUND_YET --------------------------------------------------------------- PAIR -------------------------------------------------------------------------------------------------------------------------
(b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- f : 'a * 'b -> 'c (b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- (a, b) : 'a * 'b
APP ------------------------------------------------------------------------------------------------------------------------------------------------------
(b : 'b), (a : 'a), (f : 'a * 'b -> 'c), G |- f (a, b) : 'c
FUN ----------------------------------------------------------------
(a : 'a), (f : 'a * 'b -> 'c), G |- fun b -> f (a, b) : 'b -> 'c
FUN ---------------------------------------------------------------------
(f : 'a * 'b -> 'c), G |- fun a -> fun b -> f (a, b) : 'a -> 'b -> 'c
FUN ----------------------------------------------------------------------------
G |- fun f -> fun a -> fun b -> f (a, b) : ('a * 'b -> 'c) -> 'a -> 'b -> 'c
Alfrothul: The proof tree is complete, we are done. This is the expression we were looking for.
Halcyon (mysteriously gesturing in the background): Whoosh.
Pablito: Let me check, let me check:
# fun f -> fun a -> fun b -> f (a, b);;
- : ('a * 'b -> 'c) -> 'a -> 'b -> 'c = <fun>
#
Mimer: Meet the curry function.
Dana (all of a sudden): Do we really need to construct a proof tree to devise the definition?
Anton: It sure would be nice if we didn’t.
Dana: Let’s try. The given type is ('a * 'b -> 'c) -> 'a -> 'b -> 'c, or again ('a * 'b -> 'c) -> ('a -> ('b -> 'c)) since the arrow associates to the right. So the term must start with 3 consecutive occurrences of fun:
fun ... -> fun ... -> fun ... -> ...
Alfrothul: The first formal parameter has type 'a * 'b -> 'c, which is the type of a function, so let’s pick f, and for the two others, let’s pick a and b since their type is 'a and 'b:
fun f -> fun a -> fun b -> ...
Dana: The body of the function, i.e., ..., must have type 'c so that the overall type of this expression is the given type.
Anton: We could apply f to something, and the result would be of type 'c:
fun f -> fun a -> fun b -> f ...
Dana: f expects a pair, so its argument should be one:
fun f -> fun a -> fun b -> f (..., ...)
Alfrothul: The first component of this pair must have type 'a, and the second 'b. Let’s just use a and b:
fun f -> fun a -> fun b -> f (a, b)
Anton: Look Ma, no proof tree.
Alfrothul: No explicit proof tree, yes, but this construction follows the shape of one.
Dana: I guess we are building muscle memory.
Anton: So the same construction should work for the uncurry function, no?
Alfrothul: I guess. The given type is ('a -> 'b -> 'c) -> 'a * 'b -> 'c, or again ('a -> 'b -> 'c) -> ('a * 'b -> 'c) since the arrow associates to the right. So the term must start with 2 consecutive occurrences of fun:
fun ... -> fun ... -> ...
Anton: The first formal parameter has type 'a -> 'b -> 'c, which is the type of a function, so let’s pick f, and for the other, it’s a pair, so how about we use p:
fun f -> fun p -> ...
Dana: Well, we could be more precise, since the type is 'a * 'b:
fun f -> fun (a, b) -> ...
Alfrothul: Good point. And from then on it’s the same story: the body of the function must have type 'c, so let’s apply f:
fun f -> fun (a, b) -> f ... ...
Anton: And since the first argument of f must be of type 'a and the second of type 'b, it’s not like we have any choice:
fun f -> fun (a, b) -> f a b
Alfrothul: I am liking this muscle memory.
Pablito (out of the blue): I think the curry function can be written more concisely:
# fun f a b -> f (a, b);;
- : ('a * 'b -> 'c) -> 'a -> 'b -> 'c = <fun>
#
Halcyon (fast on his feet too): So, the uncurry function...
Pablito: ...can be similarly written, yes:
# fun f (a, b) -> f a b;;
- : ('a -> 'b -> 'c) -> 'a * 'b -> 'c = <fun>
#
Halcyon (making sure): And what about functions of arity 3?
Pablito: Same same:
# fun f a b c -> f (a, b, c);;
- : ('a * 'b * 'c -> 'd) -> 'a -> 'b -> 'c -> 'd = <fun>
# fun f (a, b, c) -> f a b c;;
- : ('a -> 'b -> 'c -> 'd) -> 'a * 'b * 'c -> 'd = <fun>
#
Alfrothul: Neat extension.
Exercise 10¶
- Exhibit an expression of type 'a * 'b -> 'b * 'a. Justify your answer.
- Exhibit an expression of type ('a -> 'b) -> ('c -> 'd) -> 'a * 'c -> 'b * 'd. Justify your answer.
Exercise 11¶
- Implement the three projections for a triple.
- Implement the four projections for a quadruple.
- Implement the five projections for a quintuple.
- Short of a general implementation of projections for tuples, suggest a logical naming scheme for the projections you just implemented.
Aliasing formal parameters¶
When declaring formal parameters, we can also alias them (i.e., give them another name) using the as keyword:
Examples:
We can give two names to the same parameter:
# fun (x as y) -> (x, y);; - : 'a -> 'a * 'a = <fun> # (fun (x as y) -> (x, y)) 0;; - : int * int = (0, 0) # let (x as y) = 0 in (x, y);; - : int * int = (0, 0) #
We can give three names to the same parameter:
# fun ((x as y) as z) -> (x, y, z);; - : 'a -> 'a * 'a * 'a = <fun> # (fun ((x as y) as z) -> (x, y, z)) "hello";; - : string * string * string = ("hello", "hello", "hello") # let ((x as y) as z) = "hello" in (x, y, z);; - : string * string * string = ("hello", "hello", "hello") #We can name a pair and the components of this pair:
# fun ((a, b) as p) -> (a, b, p);; - : 'a * 'b -> 'a * 'b * ('a * 'b) = <fun> # (fun ((a, b) as p) -> (a, b, p)) (true, false);; - : bool * bool * (bool * bool) = (true, false, (true, false)) # let ((a, b) as p) = (true, false) in (a, b, p);; - : bool * bool * (bool * bool) = (true, false, (true, false)) #To wit:
LOOKUP_FOUND ------------------------------- (p : 'a * 'b), . |- p : 'a * 'b LOOKUP_FOUND ------------------------------------ LOOKUP_NOT_FOUND ----------------------------------------- (b : 'b), (p : 'a * 'b), . |- b : 'b (b : 'b), (p : 'a * 'b), . |- p : 'a * 'b LOOKUP_FOUND ---------------------------------------------- LOOKUP_NOT_FOUND ---------------------------------------------- LOOKUP_NOT_FOUND ---------------------------------------------- (a : 'a), (b : 'b), (p : 'a * 'b), . |- a : 'a (a : 'a), (b : 'b), (p : 'a * 'b), . |- b : 'b (a : 'a), (b : 'b), (p : 'a * 'b), . |- p : 'a * 'b TUPLE ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- (a : 'a), (b : 'b), (p : 'a * 'b), . |- (a, b, p) : 'a * 'b * ('a * 'b) FUN ----------------------------------------------------------------------- . |- fun ((a, b) as p) -> (a, b, p) : 'a * 'b -> 'a * 'b * ('a * 'b)We can name a triple and the components of this pair:
# fun ((a, b, c) as t) -> (a, b, c, t);; - : 'a * 'b * 'c -> 'a * 'b * 'c * ('a * 'b * 'c) = <fun> # (fun ((a, b, c) as t) -> (a, b, c, t)) (1, 2, 3);; - : int * int * int * (int * int * int) = (1, 2, 3, (1, 2, 3)) # let ((a, b, c) as t) = (1, 2, 3) in (a, b, c, t);; - : int * int * int * (int * int * int) = (1, 2, 3, (1, 2, 3)) #We can nest aliases:
# let ((x as y), ((a, b, (c as d)) as t)) = (0, (1, 2, 3)) in (x, y, a, b, c, d, t);; - : int * int * int * int * int * int * (int * int * int) = (0, 0, 1, 2, 3, 3, (1, 2, 3)) #
To wit:
INT ------------ INT ------------ INT ------------ . |- 1 : int . |- 2 : int . |- 3 : int INT ------------ TUPLE ---------------------------------------------------- LOOKUP_FOUND ----------------------------------------------------------------------------------------------------- . |- 0 : int . |- (1, 2, 3) : int * int * int (x : int), (y : int), (a : int), (b : int), (c : int), (d : int), (t : int * int * int), . |- x : int ... PAIR ------------------------------------------------------ TUPLE --------------------------------------------------------------------------------------------------------------------------------------------------------------------------- . |- (0, (1, 2, 3)) : int * (int * int * int) (x : int), (y : int), (a : int), (b : int), (c : int), (d : int), (t : int * int * int), . |- (x, y, a, b, c, d, t) : int * int * int * int * int * int * (int * int * int) LET --- . |- let ((x as y), ((a, b, (c as d)) as t)) = (0, (1, 2, 3)) in (x, y, a, b, c, d, t) : int * int * int * int * int * int * (int * int * int)
Halcyon: What. No Stevie Wonder quote?
Resources¶
- The OCaml code for the present lecture note (latest version: 02 Sep 2022).
Version¶
Added the terse analogy with onions and shallots at the end of Section Declaring several names with a local let-expression [08 Feb 2023]
Refined the description of the interactive session in Section Declaring several global names at once, based on an observation due to Ryan Lee [07 Feb 2023]
Removed the Kleene stars in the BNF [02 Feb 2023]
Polished the narrative [01 Feb 2023]
Added proof trees in Section Aliasing formal parameters [01 Feb 2023]
Added some food for thought about Exercise 09 [01 Feb 2023]
Added an interlude about functions [01 Feb 2023]
Moved Section Declaring several global names at once from Week 03 to Week 04 and expanded its narrative [01 Feb 2023]
Quantified the variables in the type-inference rules [23 Jan 2023]
Created [02 Sep 2022]