Unit tests, revisited

The goal of this lecture note is to introduce a smoother way to carry out the unit tests.

Resources

• The OCaml code for the present lecture note (latest version: 02 Sep 2022).
• The OCaml code for the present lecture note, modified (latest version: 02 Sep 2022).

Unit-test functions, more conveniently

So far we have written unit-test functions as conjunctions. For example, here is the (uncorrected) unit-test function for the factorial function as presented in the chapter about Unit tests:

let test_fac candidate =
     (candidate 0 = 1)
  && (candidate 1 = 1)
  && (candidate 2 = 2)
  && (candidate 3 = 6)
  && (candidate 4 = 24)
  && (candidate 5 = 121)
  (* etc. *);;

This notation is inconvenient for two reasons:

• it doesn’t mesh well with the default indentation provided by emacs; and
• if one of the tests fails, the result is uninformative.

For both reasons, we are better off naming the result of each test using a let-expression:

let test_fac' candidate =
  let b0 = (candidate 0 = 1)
  and b1 = (candidate 1 = 1)
  and b2 = (candidate 2 = 2)
  and b3 = (candidate 3 = 6)
  and b4 = (candidate 4 = 24)
  and b5 = (candidate 5 = 121)
  (* etc. *)
  in b0 && b1 && b2 && b3 && b4 && b5;;

This notation is more convenient for two reasons:

• it benefits from emacs’s auto-indentation; and

• in case applying test_fac to a candidate factorial function yields false, it can easily be edited to visualize which test failed by constructing a tuple of the resulting Booleans instead of computing their conjunction:

  let test_fac'' candidate =
    let b0 = (candidate 0 = 1)
    and b1 = (candidate 1 = 1)
    and b2 = (candidate 2 = 2)
    and b3 = (candidate 3 = 6)
    and b4 = (candidate 4 = 24)
    and b5 = (candidate 5 = 121)
    (* etc. *)
    in (b0, b1, b2, b3, b4, b5);;
  

In the present case, a correct candidate will fail the last test, for good reason since while 121 is the square of 11, it is not the Factorial number corresponding to 5.

Here is the corrected unit-test function for the factorial function:

let test_fac' candidate =
  let b0 = (candidate 0 = 1)
  and b1 = (candidate 1 = 1)
  and b2 = (candidate 2 = 2)
  and b3 = (candidate 3 = 6)
  and b4 = (candidate 4 = 24)
  and b5 = (candidate 5 = 120)    (* <-- correction *)
  (* etc. *)
  in b0 && b1 && b2 && b3 && b4 && b5;;

Likewise, here are the unit-test functions for the Fibonacci function (cf. Unit tests) and for boolean negation (cf. Exercise 15 in Week 03):

let test_fib candidate =
  let b0 = (candidate 0 = 0)
  and b1 = (candidate 1 = 1)
  and b2 = (candidate 2 = 1)
  and b3 = (candidate 3 = 2)
  and b4 = (candidate 4 = 3)
  and b5 = (candidate 5 = 5)
  and b6 = (candidate 6 = 8)
  (* etc. *)
  in b0 && b1 && b2 && b3 && b4 && b5 && b6;;

let test_not candidate =
  let b0 = (candidate true = false)
  and b1 = (candidate false = true)
  in b0 && b1;;

Random numbers

OCaml provides a generator of random non-negative integers such that for any non-negative integer n, applying the generator to succ n returns a random number between 0 and n:

# (Random.int 5, Random.int 5, Random.int 5, Random.int 5);;
- : int * int * int * int = (1, 2, 0, 4)
#

Whatever.

—Halcyon

Using random numbers to test the factorial function

Remembering the inductive definition of factorial numbers, i.e.,

• base case: 0! = 1
• induction step: for any natural number k, (k + 1)! = k! * (k + 1)

we can integrate them in the unit-test function for the factorial function using random numbers:

let test_fac candidate =
  (* intuitive numbers: *)
  let b1 = (candidate 1 = 1)
  and b2 = (candidate 2 = 2)
  and b3 = (candidate 3 = 6)
  and b4 = (candidate 4 = 24)
  and b5 = (candidate 5 = 120)
  (* base case: *)
  and bc = (candidate 0 = 1)
  (* random instance of the induction step: *)
  and is = (let k = Random.int 20
            in candidate (k + 1) = (candidate k) * (k + 1))
  (* etc. *)
  in b1 && b2 && b3 && b4 && b5 && bc && is;;

This unit-test function now features

• intuitive tests that make sense,
• a test that implements the base case, and
• a test that implements an instance of the induction step, for a randomly picked non-negative integer in lieu of the universally quantified variable.

A few observations:

• If the random number lies between 0 and 4, chances are the last test will be redundant compared to the previous one. On the other hand, there could be a bug in the tests over the intuitive numbers.
• It would make sense to repeat the test corresponding to the induction step.
• The unit-test function is still incomplete: it would not detect a fake factorial function that misbehaves for integers greater than 20.

Using random numbers to test expected properties

Let us revisit the function that computes a squared sum:

let square n =
  n * n;;

let squared_sum i j =
  square (i + j);;

We can strengthen its unit-test function by checking that the candidate function satisfies the binomial theorem at rank 2 as well as any algebraic identity we fancy:

let test_squared_sum candidate =
      (* intuitive numbers: *)
  let b0 = (candidate 0 0 = 0)
  and b1 = (candidate 0 1 = 1)
  and b2 = (candidate 0 2 = 4)
  and b3 = (candidate 1 0 = 1)
  and b4 = (candidate 2 0 = 4)
  and b5 = (candidate 1 2 = 9)
  and b6 = (candidate 2 1 = 9)
  and b7 = (candidate 5 5 = 100)
      (* instance of the binomial theorem at rank 2: *)
  and bt = (let i = Random.int 1000
            and j = Random.int 1000
            in candidate i j = square i + 2 * i * j + square j)
      (* twice the same integer: *)
  and twice = (let i = Random.int 1000
               in candidate i i = square (2 * i))
  (* etc. *)
  in b0 && b1 && b2 && b3 && b4 && b5 && b6 && b7 && bt && twice (* etc. *);;

But again, this unit-test function is still incomplete: it would not detect a fake function that misbehaves for integers greater than 999.

For a mouthful of other examples,

• addition is both commutative and associative, and has an identity element (namely 0);
• multiplication is both commutative and associative, and has an identity element (namely 1) as well as an absorbing element (namely 0); and
• multiplication distributes over addition.

All of these properties we can check in a unit-test function parameterized with an upper bound for the random numbers:

let test_add_mul n add mul =
      (* commutativity of addition: *)
  let a0 = (let x = Random.int n
            and y = Random.int n
            in add x y = add y x)
      (* associativity of addition: *)
  and a1 = (let x = Random.int n
            and y = Random.int n
            and z = Random.int n
            in add x (add y z) = add (add x y) z)
      (* identity element: *)
  and a2 = (let x = Random.int n
            in add 0 x = x)
  and a3 = (let x = Random.int n
            in add x 0 = x)
      (* commutativity of multiplication: *)
  and m0 = (let x = Random.int n
            and y = Random.int n
            in mul x y = mul y x)
      (* associativity of multiplication: *)
  and m1 = (let x = Random.int n
            and y = Random.int n
            and z = Random.int n
            in mul x (mul y z) = mul (mul x y) z)
      (* identity element: *)
  and m2 = (let x = Random.int n
            in mul 1 x = x)
  and m3 = (let x = Random.int n
            in mul x 1 = x)
      (* absorbing element: *)
  and m4 = (let x = Random.int n
            in mul x 0 = 0)
  and m5 = (let x = Random.int n
            in mul 0 x = 0)
      (* distributivity: *)
  and d0 = (let x = Random.int n
            and y = Random.int n
            and z = Random.int n
            in mul (add x y) z = add (mul x z) (mul y z))
  and d1 = (let x = Random.int n
            and y = Random.int n
            and z = Random.int n
            in mul x (add y z) = add (mul x y) (mul x z))
  in a0 && a1 && a2 && a3 && m0 && m1 && m2 && m3 && m4 && m5 && d0 && d1;;

For the sake of sanity, let us test this unit-test function with reference implementations of addition and multiplication:

# test_add_mul 100 ( + ) ( * );;
- : bool = true
# test_add_mul 1000 ( + ) ( * );;
- : bool = true
# test_add_mul 10000 ( + ) ( * );;
- : bool = true
#

Alfrothul: Watch these spaces.

Anton: No comments.

A character-encoding standard: ASCII

In the 1960’s, the ASCII standard was developed to represent characters as integers between 0 and 127. OCaml features two functions, int_of_char and char_of_int that map characters to their ASCII encoding and ASCII encodings to the corresponding character, respectively:

# int_of_char;;
- : char -> int = <fun>
# char_of_int;;
- : int -> char = <fun>
#

For example, the space character is encoded as 32:

# int_of_char ' ';;
- : int = 32
# char_of_int 32;;
- : char = ' '
#

One can then proceed to discover in which order other characters are encoded:

# char_of_int 33;;
- : char = '!'
# char_of_int 34;;
- : char = '"'
# char_of_int 35;;
- : char = '#'
# char_of_int 36;;
- : char = '$'
#

Ditto for brackets, be them round, square, or curly:

# int_of_char '(';;
- : int = 40
# int_of_char ')';;
- : int = 41
# int_of_char '[';;
- : int = 91
# int_of_char '\\';;
- : int = 92
# int_of_char ']';;
- : int = 93
# int_of_char '{';;
- : int = 123
# int_of_char '|';;
- : int = 124
# int_of_char '}';;
- : int = 125
#

For example, the lowercase letters are encoded consecutively and in alphabetic order:

# int_of_char 'a';;
- : int = 97
# char_of_int (int_of_char 'a' + 1);;
- : char = 'b'
# char_of_int (int_of_char 'a' + 2);;
- : char = 'c'
# char_of_int (int_of_char 'a' + 24);;
- : char = 'y'
# char_of_int (int_of_char 'a' + 25);;
- : char = 'z'
#

Ditto for the uppercase letters:

# int_of_char 'A';;
- : int = 65
# char_of_int (int_of_char 'A' + 1);;
- : char = 'B'
# char_of_int (int_of_char 'A' + 2);;
- : char = 'C'
# char_of_int (int_of_char 'A' + 25);;
- : char = 'Z'
#

Ditto for the digits:

# int_of_char '0';;
- : int = 48
# char_of_int (int_of_char '0' + 1);;
- : char = '1'
# char_of_int (int_of_char '0' + 5);;
- : char = '5'
# char_of_int (int_of_char '0' + 9);;
- : char = '9'
#

Interlude

Pablito: There is a logic, there is a logic.

Dana: Yes, Pablito?

Pablito (absorbed): Lemmesee:

# int_of_char 'a';;
- : int = 97
# int_of_char 'A';;
- : int = 65
# let shift = int_of_char 'a' - int_of_char 'A';;
val shift : int = 32
#

Halcyon (in awe): The ASCII encoding of the space character...

Dana (kindly): ...and a power of 2.

Loki mumbles something about the numerology of the ASCII table, but nobody pays attention.

Pablito (focused): That’s true. But what I am wondering is the effect of the shift key:

# char_of_int (int_of_char 'X' + shift);;
- : char = 'x'
#

Dana: Good one, Pablito.

Pablito: So what happens for the other characters?

Mimer: Don’t look too much into it, Pablito, the world has changed since the ASCII table.

Alfrothul (looking at his keyboard): Actually, not that much:

# char_of_int (int_of_char '[' + shift);;
- : char = '{'
# char_of_int (int_of_char '\\' + shift);;
- : char = '|'
# char_of_int (int_of_char ']' + shift);;
- : char = '}'
#

Halcyon (thunderingly): AHA!

Everybody jumps up.

Mimer (prudently): Yes, Halcyon?

Halcyon (regaining his, you know, suave composure): The order of characters is the order of their ASCII codes, look:

# int_of_char 'A';;
- : int = 65
# int_of_char 'a';;
- : int = 97
# 'A' < 'a';;
- : bool = true
# int_of_char '0';;
- : int = 48
# '0' < 'A';;
- : bool = true
#

Pablito: Well spotted, Halcyon!

Mimer: Yes. That was an authentic Aha! moment.

Halcyon: Thank you. Huh, feels pretty good.

Dana: It does, doesn’t it.

Exercise 12

Implement a gorgeous unit-test function for string concatenation (i.e., (^) in OCaml).

Anton: That’s at least the third time we come across these concepts.

Loki (in a funereal tone): Déjà vu. Again.

Food for thought:

• Is string concatenation commutative?
• Is string concatenation associative?
• Does string concatenation have an identity element on the left? If so, which one?
• Does string concatenation have an identity element on the right? If so, which one?
• Exercise 20 and Exercise 21 might be relevant here too.

The following two OCaml functions could come handy:

• a generator of random characters that exploits the ASCII encoding of characters as integers:

  let random_char () =
    char_of_int (Random.int 32 + int_of_char ' ');;
  

• the library function String.make that has type int -> char -> string and, when given a non-negative integer n and a character c, returns a string of length n containing c, n times:

  # String.make 2 'a';;
  - : string = "aa"
  #
  

Interlude

Anton: Could come handy?

Alfrothul: Maybe to generate a random string?

Anton: Let me try:

# String.make 2 (random_char ());;
- : string = "11"
# String.make 2 (random_char ());;
- : string = "%%"
# String.make 2 (random_char ());;
- : string = "--"
# String.make 2 (random_char ());;
- : string = "66"
#

Alfrothul: That seems to be the case. And if we modify the first argument, we should get a random string of another length:

# String.make 3 (random_char ());;
- : string = "???"
#

Anton: Huh?

Alfrothul (smiling): You mean “Huh?”? It’s just a string with 3 times the character '?'.

Anton: Harrumph. But I think I see what you mean:

# String.make 4 (random_char ());;
- : string = "<<<<"
# String.make 5 (random_char ());;
- : string = "!!!!!"
# String.make 6 (random_char ());;
- : string = "......"
#

Alfrothul: OK. So we can manufacture a string of a given length containing repeated occurrences of the same random character. We could even implement a function to do that:

let random_string n =
  String.make n (random_char ());;

Anton: Well, OCaml says it has type int -> string.

Alfrothul: And it works too:

# random_string 2;;
- : string = "44"
# random_string 3;;
- : string = "%%%"
# random_string 4;;
- : string = "9999"
#

Anton: What if we apply random_string to 0?

Dana: It’s not going to be very random, is it.

Alfrothul: Well, there is only one string of length 0, and it is the empty string, so, yes, not random at all:

# random_string 0;;
- : string = ""
# random_string 0;;
- : string = ""
# random_string 0;;
- : string = ""
#

Anton: On the other hand, we could generate strings of random length:

# random_string (Random.int 10);;
- : string = "   "
# random_string (Random.int 10);;
- : string = "######"
# random_string (Random.int 10);;
- : string = ""
# random_string (Random.int 10);;
- : string = "<<<<<<<<<"
#

Alfrothul: We might as well bake that in the definition of random_string:

let random_string n =
  String.make (Random.int n) (random_char ());;

Anton: That should work:

# random_string 20;;
- : string = "0000000000000000000"
# random_string 20;;
- : string = "//////////"
# random_string 20;;
- : string = "444"
# random_string 20;;
- : string = "444444"
#

Alfrothul: OK. So we now have a function that, given a positive integer, returns a string of random length containing repeated occurrences of the same random character.

Loki (ever the helpful one): And now you are equipped to test whether string concatenation is commutative, for example.

Assertions

OCaml features assert-expressions:

<expression> ::= ...
               | assert <expression>

If e evaluates to true, then assert e evaluates to (), and if e evaluates to false, then OCaml complains:

# assert true;;
- : unit = ()
# assert false;;
Exception: Assert_failure ("//toplevel//", 1573, -52).
#

We can thus treat our unit tests as assertions: if a function passes its unit tests, we don’t want to hear about it, whereas if it doesn’t, we very much do. For example:

# let () = assert (test_successor (fun n -> n + 1) = true);;
# let () = assert (test_successor (fun n -> n) = true);;
Exception: Assert_failure ("//toplevel//", 1573, -43).
#

The second assertion fails because the identity function does not pass the unit tests for the successor function.

More concisely, but less helpfully, we can write:

# let () = assert (test_successor (fun n -> n + 1));;
# let () = assert (test_successor (fun n -> n));;
Exception: Assert_failure ("//toplevel//", 1573, -43).
#

So from now on, instead of writing comments in our .ml files to the effect that a function passes its unit test, we will simply assert that they do:

let () = assert (test_successor (fun n -> n + 1) = true);;

And when the file is loaded, we will be alerted if a function does not pass its unit tests.

In other words, from now on, what goes well goes without showing.

A concrete example

As a concrete example, download the resource file, edit it using Emacs in Tuareg mode, load it in OCaml (by typing #use "week-04_unit-tests.ml"), and observe how:

• test_successor is defined,
• successor_v0 is defined and silently passes the unit test,
• successor_v0' is defined and silently passes the unit test,
• successor_v1 is defined and silently passes the unit test,
• successor_v1' is defined and silently passes the unit test,
• identity' is defined and fails to pass the unit test, and
• the last thing that is printed is the name of the file.

Namely:

# #use "week-04_unit-tests.ml";;
val test_successor : (int -> int) -> bool = <fun>
val successor_v0 : int -> int = <fun>
val successor_v0' : int -> int = <fun>
val successor_v1 : int -> int = <fun>
val successor_v1' : int -> int = <fun>
val identity : 'a -> 'a = <fun>
Exception: Assert_failure ("week-04_unit-tests.ml", 45, 9).
#

The error message tells us that at Line 45, the assertion is not satisfied. (To be precise, the expression assert (test_successor identity = true);; starts at Column 9 of Line 45.)

Expected failures

Sometimes, it is useful to verify that a test fails. In the present case, since we expect that identity will not pass the unit test for the successor function, we can state this as such in the file, and write:

let () = assert (test_successor identity = false);;

instead of:

let () = assert (test_successor identity);;

The resulting modified file loads without any hiccup:

# #use "week-04_unit-tests-modified.ml";;
val test_successor : (int -> int) -> bool = <fun>
val successor_v0 : int -> int = <fun>
val successor_v0' : int -> int = <fun>
val successor_v1 : int -> int = <fun>
val successor_v1' : int -> int = <fun>
val identity : 'a -> 'a = <fun>
- : string = "week-04_unit-tests-modified.ml"
#

Recommended way to compose .ml files

The recommended way to compose one’s .ml file is as follows:

• start with (* name-of-the-file.ml *),
• continue with some identifying data, e.g., your name and a date for the current version,
• define a unit-test function,
• define a first version of a function and assert that it passes the unit test,
• define a second version of a function and assert that it passes the unit test,
• define a third version of a function and assert that it passes the unit test,
• etc.
• write let end_of_file = "name-of-the-file.ml";;, and
• add the digital signature, i.e., a comment that contains what OCaml prints out when it is started afresh and the file is loaded.

This way, the unit tests will be run every time the file is loaded, and in the end, the digital signature will witness that the file was successively and completely loaded.

Exercise 13

1. What does it mean for a .ml file to be digitally signed?
2. What guarantee does a digital signature provide?

Exercise 14

The goal of this exercise is to check whether the following .ml files contain a valid digital signature. Justify your answer and fix the digital signature if it is invalid.

1. week-04_example-a.ml.
2. week-04_example-b.ml.
3. week-04_example-c.ml.

Exercise 15

This exercise assumes that the reader is convinced that unit tests are A Good Thing, and that it is Very Useful to compose one’s .ml file as recommended above, so that (1) the unit-test functions are written before the functions to test are implemented, and (2) the implemented functions are automatically tested when the file is loaded, which guarantees that the latest version of the implementation is tested.

Under this assumption, and besides the fact that the identity function fails the unit test for the successor function, there is an all-too-common error both in this resource file and in this modified resource file. What is this embarrassing error?

Shielding unit tests

Assertions make it possible to verify in passing that conditions are satisfied. For example, the implementation of test_add_mul expects its first argument to be a positive integer. That it is an integer is a typing property, and this property is therefore ensured by OCaml’s type system. But there is no type for positive integers, and therefore this implementation is vulnerable to non-positive integers:

# test_add_mul 0 ( + ) ( * );;
Exception: Invalid_argument "Random.int".
# test_add_mul ~-1 ( + ) ( * );;
Exception: Invalid_argument "Random.int".
#

The error message reports how things went wrong in the implementation of test_add_mul, which is uninformative to the user. It would be more informative to report what went wrong at the point where it went wrong. To this end, let us insert an assertion at the outset of the implementation:

let test_add_mul n add mul =
  let () = assert (n > 0) in
      (* commutativity of addition: *)
  let a0 = ...

This unit-test function was vulnerable to being applied to a non-positive integer. It is now shielded.

Exercise 16

You are given the following OCaml functions:

let power_0 x = (* computes x^0 *)
  1;;

let power_1 x = (* computes x^1 *)
  x;;

let power_2 x = (* computes x^2 *)
  x * x;;

let power_3 x = (* computes x^3 *)
  x * x * x;;

let power_4 x = (* computes x^4 *)
  x * x * x * x;;

In this exercise, we do not worry about OCaml’s fixed-size arithmetic, i.e., that only finitely many integers are representable.

1. implement a function that given an integer x, computes the polynomial 4 * x^4 + 3 * x^3 + 2 * x^2 + 1 * x^1 + 0 * x^0:

   let p x =
     ...
   

2. implement a function that, given an integer x, computes the same polynomial using Horner’s rule, i.e., (((4 * x + 3) * x + 2) * x + 1) * x + 0:

   let h x =
     ...
   

3. implement a simple unit-test function that verifies whether your two implementations of the polynomial are equivalent:

   let test_polynomials candidate_1 candidate_2 =
     let b0 = (candidate_1 0 = candidate_2 0)
     and ...
     in b0 & ...;;
   

   In other words, test_polynomials p h should evaluate to true.

4. implement a fake polynomial function that passes your unit test (i.e., that seems equivalent to either of your implementations) but that is incorrect:

   let fake_polynomial x =
     ...
   

   In other words, both test_polynomials p fake_polynomial and test_polynomials fake_polynomial h should evaluate to true.

5. strengthen your unit-test function using Random.int, as in the section about Using random numbers to test the factorial function:

   let test_polynomials_more_strongly candidate_1 candidate_2 =
     let b0 = (candidate_1 0 = candidate_2 0)
     and ...
     and br = (let x = Random.int ...
               in candidate_1 x = candidate_2 x)
     in b0 & ... & br;;
   

   so that it defeats fake_polynomial

   In other words, both test_polynomials_more_strongly p fake_polynomial and test_polynomials_more_strongly fake_polynomial h should evaluate to false.

   Food for thought:

   • should they always evaluate to false?
   • might they sometimes evaluate to true?

6. implement a more devious fake polynomial function that cheats your strengthened unit-test function:

   let faker_polynomial x =
     ...
   

   In other words, both test_polynomials_more_strongly p faker_polynomial and test_polynomials_more_strongly faker_polynomial h should evaluate to true.

7. strengthen even more your unit-test function by parameterizing it with the argument of Random.int:

   let test_polynomials_even_more_strongly candidate_1 candidate_2 n =
     let b0 = (candidate_1 0 = candidate_2 0)
     and ...
     and br = (let x = Random.int n
               in candidate_1 x = candidate_2 x)
     in b0 & ... & br;;
   

   Use this new unit-test function to defeat faker_polynomial.

8. can you implement an even more devious polynomial function that cheats test_polynomials_even_more_strongly?

   Justify your answer with an implementation:

   let fakest_polynomial x =
     ...
   

   or with an explanation.

Anton: Plenty of opportunities to quote Dijkstra here.

Alfrothul: Yes. It’s a rite of passage.

Interlude about style

Pablito: When writing a local let expression, where should we put the in?

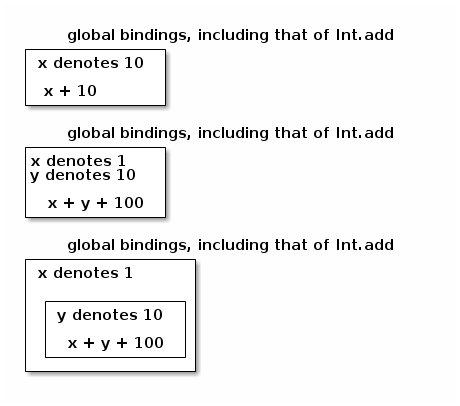
Anton: The lecture notes are very uniform about that positioning. The in is vertically aligned with the let:

let x = 1
in x + 10;;

let x = 1
and y = 10
in x + y + 100;;

let (x, y) = (1, 10)
in x + y + 100;;

let x = 1
in let y = 10
   in x + y + 100;;

Alfrothul: This way, the nested boxes depicting lexical scope are easy to draw mentally:

Dana: And when the local let-expression doesn’t extend the environment, there is no reason to align in vertically with the let. For example, if we want to make sure that the argument of a function is non-negative, we write:

let foo n =
  let () = assert (n >= 0) in
  ...

‘But’ is the way of asking for permission to lay something heavy on one’s head.

—Stevie Wonder

Pablito: But...

Dana: Yes?

Pablito: Well, I read a manual of OCaml style somewhere, and it said that if the let-expression declares only one binding, in should be put at the end of the line, not on the next line.

Mimer: Right. Think of it as the training wheels on a child’s first bicycle. The goal here is to make you associate nested lexical blocks with nested let-expressions. Once this association is clear in your mind, the training wheels can go.

Pablito: OK, thanks.

Resources

• The OCaml code for the present lecture note (latest version: 02 Sep 2022).
• The OCaml code for the present lecture note, modified (latest version: 02 Sep 2022).
• The OCaml code for Exercise 12 and Exercise 16 (latest version: 02 Sep 2022).

Version

Expanded the interlude about the logic of the ASCII table [12 Mar 2023]

Stated that the instance of the induction step was random in test_fac [04 Mar 2023]

Added Halcyon’s Aha! moment about the ordering of characters in OCaml [12 Feb 2023]

Added Section A character-encoding standard: ASCII and the following interlude [10 Feb 2023]

Adjusted the .ml files of Exercise 15 [03 Feb 2023]

Added Exercise 13 and Exercise 14 [23 Jan 2023]

Created [02 Sep 2022]