The Art of Computer Science¶
So data represent information, and are processed to obtain new data, which represent new information:
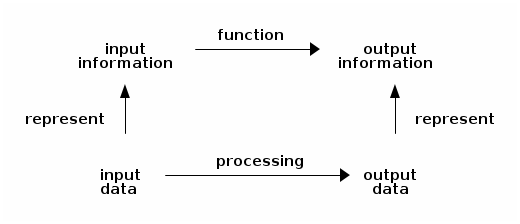
The processing is carried out by a program that computes a function.
The art of Computer Science is to choose a representation that is preferably sound and complete, and that enables an implementation that is preferably sound and complete (i.e., correct) as well as efficient.
Early optimization is the source of a lot of evil.
Resources¶
- The OCaml code for the present lecture note (latest version: 07 Mar 2019).
Representing finite sets as lists without repetitions, Take 0¶
Take our earlier implementation of finite sets as lists of their elements without repetition, for example. This representation is sound because constructing a list of distinct elements represents a finite set, and it is complete because any finite set can be represented as a list of distinct elements.
Then implementing the union function is pretty direct, since a set is either empty or it is the union of a singleton set and another set:
let belongs_to e es =
let rec visit es =
match es with
| [] ->
false
| e' :: es' ->
if e = e'
then true
else visit es'
in visit es;;
let set_union_v0 e1s e2s =
let rec visit e1s =
match e1s with
| [] ->
e2s
| e1 :: e1s' ->
let ih = visit e1s'
in if belongs_to e1 ih
then ih
else e1 :: ih
in visit e1s;;
This implementation of set union is direct but it is also inefficient since in the course of the recursive calls, each element of the first set will be tested on a growing set that extends the second set with elements of the first set:
# traced_set_union_v0 show_int [1; 2; 3; 4] [5];;
set_union [1; 2; 3; 4] [5] ->
visit [1; 2; 3; 4] [5] ->
visit [2; 3; 4] [5] ->
visit [3; 4] [5] ->
visit [4] [5] ->
visit [] [5] ->
visit [] [5] <- [5]
belongs_to 4 [5] ->
belongs_to 4 [] ->
belongs_to 4 [] <- false
visit [4] [5] <- [4; 5]
belongs_to 3 [4; 5] ->
belongs_to 3 [5] ->
belongs_to 3 [] ->
belongs_to 3 [] <- false
visit [3; 4] [5] <- [3; 4; 5]
belongs_to 2 [3; 4; 5] ->
belongs_to 2 [4; 5] ->
belongs_to 2 [5] ->
belongs_to 2 [] ->
belongs_to 2 [] <- false
visit [2; 3; 4] [5] <- [2; 3; 4; 5]
belongs_to 1 [2; 3; 4; 5] ->
belongs_to 1 [3; 4; 5] ->
belongs_to 1 [4; 5] ->
belongs_to 1 [5] ->
belongs_to 1 [] ->
belongs_to 1 [] <- false
visit [1; 2; 3; 4] [5] <- [1; 2; 3; 4; 5]
set_union [1; 2; 3; 4] [5] <- [1; 2; 3; 4; 5]
- : int list = [1; 2; 3; 4; 5]
#
That is silly because since the first argument of set_union_v0 represents a set, it contains no duplications and indeed in the trace above, all the calls to belongs_to yield false since the two arguments are disjoint sets.
So a better implementation only tests whether each successive element of the first set belongs to the second set:
let set_union_v1 e1s e2s =
let rec visit e1s =
match e1s with
| [] ->
e2s
| e1 :: e1s' ->
let ih = visit e1s'
in if belongs_to e1 e2s
then ih
else e1 :: ih
in visit e1s;;
And indeed each element of the first set is only be tested on the second set:
# traced_set_union_v1 show_int [1; 2; 3; 4] [5];;
set_union [1; 2; 3; 4] [5] ->
visit [1; 2; 3; 4] [5] ->
visit [2; 3; 4] [5] ->
visit [3; 4] [5] ->
visit [4] [5] ->
visit [] [5] ->
visit [] [5] <- [5]
belongs_to 4 [5] ->
belongs_to 4 [] ->
belongs_to 4 [] <- false
visit [4] [5] <- [4; 5]
belongs_to 3 [5] ->
belongs_to 3 [] ->
belongs_to 3 [] <- false
visit [3; 4] [5] <- [3; 4; 5]
belongs_to 2 [5] ->
belongs_to 2 [] ->
belongs_to 2 [] <- false
visit [2; 3; 4] [5] <- [2; 3; 4; 5]
belongs_to 1 [5] ->
belongs_to 1 [] ->
belongs_to 1 [] <- false
visit [1; 2; 3; 4] [5] <- [1; 2; 3; 4; 5]
set_union [1; 2; 3; 4] [5] <- [1; 2; 3; 4; 5]
- : int list = [1; 2; 3; 4; 5]
#
The mindful programmer observes that in the definition of set_union_v1, the recursive call to visit and the call to belongs_to are independent. Unfolding the let-expression leads to a combination of tail-calls and non-tail calls that was the topic of Exercise 4 and Exercise 5 as well as of the intervening interludes:
let set_union_v2 e1s e2s =
let rec visit e1s =
match e1s with
| [] ->
e2s
| e1 :: e1s' ->
if belongs_to e1 e2s
then visit e1s'
else e1 :: visit e1s'
in visit e1s;;
Since tail calls consume fewer computational resources than non-tail calls, that is another win in the implementation.
And then since the order of elements in the resulting set does not matter, the mindful programmer uses an accumulator to obtain an iterative implementation of set union (see Exercise 3).
To sum up, a representation was chosen, and then an increasingly efficient computation was designed.
Yet in the worst case, the two sets are disjoint and so for each element of the first set, belongs_to has to traverse the entirety of the second set.
Representing finite sets as lists without repetitions, Take 1¶
If the elements of the sets under consideration are totally ordered, one can represent these sets as an ordered list. Then testing whether an element occurs in a set, on average, does not require traversing all this set – it can stop as soon as a larger element is encountered. That was the point of Exercise 16.
To sum up, an alternative representation was chosen, and then an increasingly efficient computation was designed.
Yet in the worst case, all the elements of the first set are larger than all the elements of the second set, and so for each element of the first set, belongs_to has to traverse the entirety of the second set.
Representing finite sets as binary trees without repetitions, Take 0¶
In order to overcome this worst-case linearity, the mindful programmer represents a finite set as a binary tree with payloads in the nodes and in the leaves, where for each node, all the elements in the left subtree of this node are smaller than the element in the node, and all the elements of the right subtree are larger. This way, on average, for a set of n elements, we can test whether an element occurs in this set in log2(n) steps.
To sum up, a new representation was chosen, and then a more efficient computation was designed.
Yet in the worst case, the binary tree is not balanced, and we are back to a linear complexity.
Representing finite sets as binary trees without repetitions, Take 1¶
In order to overcome this worst-case linearity, the mindful programmer represents a finite set as a balanced binary tree with payloads in the nodes and in the leaves, where for each node, all the elements in the left subtree of this node are smaller than the element in the node, and all the elements of the right subtree are larger. This way, even in the worst case, for a set of n elements, we can test whether an element occurs in this set in log2(n) steps.
The requirement over the representation is more stringent, and requires each binary tree to adapt to the addition and deletion of elements in order to remained balanced.
To sum up, a dynamic (instead of static) representation was chosen, and then an even more efficient computation was designed.
The turning point: from linear to logarithmic¶
There is something Hegelian in the process described so far: we design a representation, develop a computation to process it, refine this computation, design an alternative representation, develop a computation to process it, refine this computation, etc. Therein, however, lies the art of computer science.
That said, the turning point in this Hegelian process was the move from linear to logarithmic.
As it turns out, natural numbers offer representational support for such a move.
Natural numbers, revisited: from mathematical induction (in base 1) to structural induction (in base 2)¶
So far, we have considered Peano numbers, i.e., natural numbers in base 1. This representational choice, which corresponds to mathematical induction, has mechanically determined a linear complexity to the resulting programs. Indeed for any given natural number, the number of successive decrements it takes to reach 0 coincides with this natural number.
Representing natural numbers in base 2 would determine a logarithmic complexity, since we would process them by successive divisions by 2. Indeed for any given natural number, the number of successive divisions by 2 it takes to reach 0 is the logarithm (in base 2) of this given number.
Exercise 21¶
On the ground that for any non-negative integers x1 and x2 (represented as x1 and x2), the following equations hold:
0 + x2 = x2
x1 + 0 = x1
2 * (succ x1) + 2 * (succ x2) = 2 * ((succ x1) + (succ x2))
2 * x1 + 1 + 2 * (succ x2) = 2 * (x1 + (succ x2)) + 1
2 * (succ x1) + 2 * x2 + 1 = 2 * ((succ x1) + x2) + 1
2 * x1 + 1 + 2 * x2 + 1 = 2 * (x1 + x2 + 1)
implement an addition function that proceeds by successive divisions by 2 of its arguments.
Solution for Exercise 21¶
In the equations, the cases zero / not zero are accounted with 0 / succ x, for some natural number x.
The two first equations account for either x1 and x2 being 0.
The remaining four equations enumerate the addition of positive natural numbers (the presence of succ is to convey that the even number is positive):
- two even numbers,
- one odd number and one even number,
- one even number and one odd number, and
- two odd numbers.
These six equations are exhaustive.
So all we need to do is to enumerate these possibilities while successively halving the two given integers:
let add2 x1 x2 =
let () = assert (x1 >= 0 && x2 >= 0) in
let rec visit x1 x2 =
if x1 = 0
then x2
else (if x2 = 0
then x1
else let q1 = x1 / 2
and r1 = x1 mod 2
and q2 = x2 / 2
and r2 = x2 mod 2
in if r1 = 0
then (if r2 = 0
then 2 * (visit q1 q2)
else succ (2 * (visit q1 q2)))
else (if r2 = 0
then succ (2 * (visit q1 q2))
else 2 * (succ (visit q1 q2))))
in visit x1 x2;;
Halcyon: Ta-da!
When repeatedly dividing a natural number by 2, the number of times it takes to reach 0 is the logarithm (in base 2) of this natural number. Therefore, add2 proceeds in logarithmically many recursive calls over the smallest of its two arguments.
The accompanying resource file also contains a traced version. This traced version makes it possible to visualize the successive divisions by 2:
# traced_add2 123456 654321;;
add2 123456 654321 ->
visit 123456 654321 ->
visit 61728 327160 ->
visit 30864 163580 ->
visit 15432 81790 ->
visit 7716 40895 ->
visit 3858 20447 ->
visit 1929 10223 ->
visit 964 5111 ->
visit 482 2555 ->
visit 241 1277 ->
visit 120 638 ->
visit 60 319 ->
visit 30 159 ->
visit 15 79 ->
visit 7 39 ->
visit 3 19 ->
visit 1 9 ->
visit 0 4 ->
visit 0 4 <- 4
visit 1 9 <- 10
visit 3 19 <- 22
visit 7 39 <- 46
visit 15 79 <- 94
visit 30 159 <- 189
visit 60 319 <- 379
visit 120 638 <- 758
visit 241 1277 <- 1518
visit 482 2555 <- 3037
visit 964 5111 <- 6075
visit 1929 10223 <- 12152
visit 3858 20447 <- 24305
visit 7716 40895 <- 48611
visit 15432 81790 <- 97222
visit 30864 163580 <- 194444
visit 61728 327160 <- 388888
visit 123456 654321 <- 777777
add2 123456 654321 <- 777777
- : int = 777777
#
More tellingly, let us add two powers of 2, using a linear-time power function also found in the accompanying resource file:
# traced_add2 (power1 2 10) (power1 2 10);;
add2 1024 1024 ->
visit 1024 1024 ->
visit 512 512 ->
visit 256 256 ->
visit 128 128 ->
visit 64 64 ->
visit 32 32 ->
visit 16 16 ->
visit 8 8 ->
visit 4 4 ->
visit 2 2 ->
visit 1 1 ->
visit 0 0 ->
visit 0 0 <- 0
visit 1 1 <- 2
visit 2 2 <- 4
visit 4 4 <- 8
visit 8 8 <- 16
visit 16 16 <- 32
visit 32 32 <- 64
visit 64 64 <- 128
visit 128 128 <- 256
visit 256 256 <- 512
visit 512 512 <- 1024
visit 1024 1024 <- 2048
add2 1024 1024 <- 2048
- : int = 2048
#
Adding powers of 2 makes it simple to visualize how the computation proceeds in logarithmically many recursive calls to visit – 11 above to reach the base case (from 10 to 0) and 6 below (from 5 to 0):
# traced_add2 (power1 2 5) (power1 2 10);;
add2 32 1024 ->
visit 32 1024 ->
visit 16 512 ->
visit 8 256 ->
visit 4 128 ->
visit 2 64 ->
visit 1 32 ->
visit 0 16 ->
visit 0 16 <- 16
visit 1 32 <- 33
visit 2 64 <- 66
visit 4 128 <- 132
visit 8 256 <- 264
visit 16 512 <- 528
visit 32 1024 <- 1056
add2 32 1024 <- 1056
- : int = 1056
# traced_add2 (power1 2 10) (power1 2 5);;
add2 1024 32 ->
visit 1024 32 ->
visit 512 16 ->
visit 256 8 ->
visit 128 4 ->
visit 64 2 ->
visit 32 1 ->
visit 16 0 ->
visit 16 0 <- 16
visit 32 1 <- 33
visit 64 2 <- 66
visit 128 4 <- 132
visit 256 8 <- 264
visit 512 16 <- 528
visit 1024 32 <- 1056
add2 1024 32 <- 1056
- : int = 1056
#
Exercise 22¶
On the ground that for any non-negative integers x1 and x2 (represented as x1 and x2), the following equations hold:
0 * x2 = 0
x1 * 0 = 0
(2 * (succ x1)) * x2 = 2 * ((succ x1) * x2)
(2 * x1 + 1) * (2 * (succ x2)) = 2 * ((2 * x1 + 1) * (succ x2))
(2 * x1 + 1) * (2 * x2 + 1) = 4 * (x1 * x2) + 2 * (x1 + x2) + 1
implement a multiplication function that proceeds by successive divisions by 2 of its arguments.
Solution for Exercise 22¶
In the equations, the cases zero / not zero are accounted with 0 / succ x, for some natural number x.
The two first equations account for either x1 and x2 being 0.
The remaining three equations enumerate the multiplication of positive natural numbers (the presence of succ is to convey that the even number is positive):
- an even number and another number,
- an odd number and an even number,
- two odd numbers.
These five equations are exhaustive.
So all we need to do is to enumerate these possibilities while successively halving the two given integers:
let mul2 x1 x2 =
let () = assert (x1 >= 0 && x2 >= 0) in
let rec visit1 x1 x2 =
if x1 = 0
then 0
else let q1 = x1 / 2
and r1 = x1 mod 2
in if r1 = 0
then 2 * (visit1 q1 x2)
else visit2 q1 x2
and visit2 q1 x2 =
if x2 = 0
then 0
else let q2 = x2 / 2
and r2 = x2 mod 2
in if r2 = 0
then 2 * (visit2 q1 q2)
else 4 * (visit1 q1 q2) + 2 * (q1 + q2) + 1
in visit1 x1 x2;;
Analysis:
- visit1 successively halves the first argument until it reaches an odd number, at which point it tail-calls visit2
- visit2 successively halves the second argument until it reaches an odd number, at which point it calls visit1.
Zeno: And yet you guys don’t know the half of it.Mimer: Maybe so, but did you really need to go there?
When repeatedly dividing a natural number by 2, the number of times it takes to reach 0 is the logarithm (in base 2) of this natural number. Therefore, mul2 proceeds in logarithmically many recursive calls over the product of its two arguments (since log(x1) + log(x2) = log(x1 * x2)).
The accompanying resource file also contains a traced version. This traced version makes it possible to visualize the successive divisions by 2:
# traced_mul2 1111 111;;
..mul2 1111 111 ->
visit1 1111 111 ->
visit2 555 111 ->
visit1 555 55 ->
visit2 277 55 ->
visit1 277 27 ->
visit2 138 27 ->
visit1 138 13 ->
visit1 69 13 ->
visit2 34 13 ->
visit1 34 6 ->
visit1 17 6 ->
visit2 8 6 ->
visit2 8 3 ->
visit1 8 1 ->
visit1 4 1 ->
visit1 2 1 ->
visit1 1 1 ->
visit2 0 1 ->
visit1 0 0 ->
visit1 0 0 <- 0
visit2 0 1 <- 1
visit1 1 1 <- 1
visit1 2 1 <- 2
visit1 4 1 <- 4
visit1 8 1 <- 8
visit2 8 3 <- 51
visit2 8 6 <- 102
visit1 17 6 <- 102
visit1 34 6 <- 204
visit2 34 13 <- 897
visit1 69 13 <- 897
visit1 138 13 <- 1794
visit2 138 27 <- 7479
visit1 277 27 <- 7479
visit2 277 55 <- 30525
visit1 555 55 <- 30525
visit2 555 111 <- 123321
visit1 1111 111 <- 123321
..mul2 1111 111 <- 123321
- : int = 123321
#
More tellingly, let us multiply two powers of 2, using the linear-time power function also found in the accompanying resource file:
# traced_mul2 (power1 2 4) (power1 2 6);;
..mul2 16 64 ->
visit1 16 64 ->
visit1 8 64 ->
visit1 4 64 ->
visit1 2 64 ->
visit1 1 64 ->
visit2 0 64 ->
visit2 0 32 ->
visit2 0 16 ->
visit2 0 8 ->
visit2 0 4 ->
visit2 0 2 ->
visit2 0 1 ->
visit1 0 0 ->
visit1 0 0 <- 0
visit2 0 1 <- 1
visit2 0 2 <- 2
visit2 0 4 <- 4
visit2 0 8 <- 8
visit2 0 16 <- 16
visit2 0 32 <- 32
visit2 0 64 <- 64
visit1 1 64 <- 64
visit1 2 64 <- 128
visit1 4 64 <- 256
visit1 8 64 <- 512
visit1 16 64 <- 1024
..mul2 16 64 <- 1024
- : int = 1024
#
Exercise 23¶
We are given the following square function:
let square x =
x * x;;
On the ground that for any integer x (represented as x) and natural number n (represented as n), the following equations hold:
x^0 = 1 x^(2 * (succ n)) = (x^2)^(succ n) x^(2 * n + 1) = (x^2)^n * x
implement a power function that proceeds by successive divisions by 2 and that exploits these equations:
let power_v0 x n = (* power_v0 : int -> int -> int *) let () = assert (n >= 0) in ...
Since multiplication is commutative, the equations above can also be written as follows:
x^0 = 1 x^(2 * (succ n)) = (x^(succ n))^2 x^(2 * n + 1) = (x^n)^2 * x
Implement another power function that proceeds by successive divisions by 2 and that exploits these alternative equations:
let power_v1 x n = (* power_v1 : int -> int -> int *) let () = assert (n >= 0) in ...
Any thoughts about these two versions of the power function?
Resources¶
- The OCaml code for the present lecture note (latest version: 07 Mar 2019).