Exercises for Week 04

Exercise 00

1. The index of concepts for this week is in a separate chapter. Peruse it and make sure that its entries make sense to you (otherwise, click on them to check them out).

2. The lecture notes start with updates (Chapter Lecture Notes, updates). Make sure to check them out regularly, as they reflect the development of the lecture.

3. Briefly explain, in your own words, the concept of commuting diagram, as presented in the postlude of Chapter Towards OCaml.

   For one more example (which could be connected to Exercise 08.i):

   

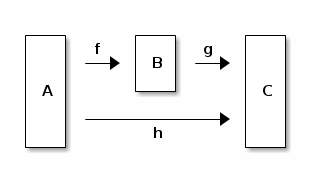
4. What does it mean for a name to “shadow” another one?

5. For your general culture, check out the author’s tribute to Peter Landin.

Resources

• A template .ml file for the exercises of this week (latest version: 19 Mar 2023).

Mandatory exercises

• Exercise 00: perusing the index and checking the updates
• Exercise 03: implementing and testing disjunction of Booleans
• Exercise 06: implementing and testing exclusive disjunction of Booleans
• Exercise 07: exhibiting expressions of a given polymorphic type
• Exercise 08: exhibiting more expressions of a given polymorphic type
• Exercise 09: lexical scope at work
• Exercise 13: what is a digital signature?
• Exercise 14: valid and invalid digital signatures
• Exercise 15: an all-too-common error
• Exercise 16: implementing and testing polynomials of degree 4
• Exercise 17: tinkering with the generator of random proofs
• Exercise 19: associating left and right

Recommended exercises

• Exercise 10: exhibiting even more expressions of a given polymorphic type
• Exercise 12: a gorgeous unit-test function for string concatenation

Exercises for the over-achievers (this means you)

• Exercise 22: exhibiting a family of expressions of a family of given types; did we see these types before?
• Exercise 23: Landin’s principle of correspendence between names declared in a let-expression and names declared in a function abstraction
• Exercise 24: Landin’s principle of correspendence revisited

Exercise 19

A question about the design of OCaml:

• in its language of expressions, applications implicitly associate to the left, i.e., String.get "hello world" 0 is parsed as (String.get "hello world") 0;
• in its language of types, function types implicitly associate to the right, i.e., string -> int -> char is parsed as string -> (int -> char).

Justify this choice.

Pablito: Hum. Could we be given the smudge of a hint?

The fourth wall: An interlude with no warning now?

Pablito: Sor-ry!

Smudge of a hint about Exercise 19 in the form of an interlude

Pablito: OK now?

The fourth wall: Yes, thanks.

Pablito: So, huh, could we have a hint about Exercise 19?

Mimer: Of course. Contemplate the APP typing rule.

Richard Feynman: I believe that has some significance for [y]our problem.

Mimer: Professor Feynman! Thanks for stopping by!

Halcyon (whispering to Pablito): Is he joking? Mr. Feynman I mean.

Pablito (whispering back): I am not sure.

Mimer: Huh, by the by, would you mind autographing my copy of your book?

Exercise 20

Consider the following definition:

let length_of_string_self_concatenation s =
  String.length (s ^ s) = 2 * String.length s;;

What is the result of applying length_of_string_concatenation to any string?

• true, always?
• false, always?
• sometimes true, sometimes false?

Justify your answer.

Solution for Exercise 20

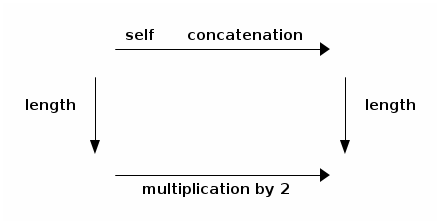
The answer is true, always, because concatenating a string to itself yields a string which is twice as long.

The computation carried out by length_of_string_self_concatenation can be depicted with the following commuting diagram:

Exercise 21

Consider the following definition:

let length_of_string_concatenation s1 s2 =
  String.length (s1 ^ s2) = String.length s1 + String.length s2;;

What is the result of applying length_of_string_concatenation to any two strings?

• true, always?
• false, always?
• sometimes true, sometimes false?

Justify your answer.

Exercise 22

1. Exhibit an expression of type ('a * 'b * 'c * 'd * 'e -> 'f) -> unit -> 'a * 'b * 'c * 'd * 'e -> 'f. Justify your answer.
2. Exhibit an expression of type ('a * 'b * 'c * 'd * 'e -> 'f) -> 'a -> 'b * 'c * 'd * 'e -> 'f. Justify your answer.
3. Exhibit an expression of type ('a * 'b * 'c * 'd * 'e -> 'f) -> 'a * 'b -> 'c * 'd * 'e -> 'f. Justify your answer.
4. Exhibit an expression of type ('a * 'b * 'c * 'd * 'e -> 'f) -> 'a * 'b * 'c -> 'd * 'e -> 'f. Justify your answer.
5. Exhibit an expression of type ('a * 'b * 'c * 'd * 'e -> 'f) -> 'a * 'b * 'c * 'd -> 'e -> 'f. Justify your answer.
6. Exhibit an expression of type ('a * 'b * 'c * 'd * 'e -> 'f) -> 'a * 'b * 'c * 'd * 'e -> unit -> 'f. Justify your answer.

Déjà vu, anyone?

Strange.

—Grace Jones

Exercise 23

Let us revisit the FUN, APP, and LET typing rules:

FUN	G, (x1 : t1) |- e2 : t2
	G |- fun x1 -> e2 : t1 -> t2

APP	G |- e0 : t1 -> t2	G |- e1 : t1
	G |- e0 e1 : t2

LET	G |- e1 : t1	(x1 : t1), G |- e2 : t2
	G |- let x1 = e1 in e2 : t2

For the sake of this exercise, let us assume that for any name x1 and for any expression e1 and e2, a let-expression such as let x1 = e1 in e2 is syntactic sugar for (fun x1 -> e2) e1, a principle of correspondence due to Peter Landin. Is this syntactic sugar compatible with the typing rules just above? In other words, can the LET typing rule be derived out of the FUN and APP typing rules?

Postlude

This presentation of let-expressions is a simplified one. In actuality, let-expressions are the way to introduce polymorphism in OCaml:

# let identity = fun x -> x in (identity 1, identity true);;
- : int * bool = (1, true)
# (fun identity -> (identity 1, identity true)) (fun x -> x);;
Characters 39-43:
  (fun identity -> (identity 1, identity true)) (fun x -> x);;
                                         ^^^^
Error: This expression has type bool but an expression was expected of type
         int
#

And so when constructing the proof tree for an expression that involves a let-expression, in practice, we duplicate the declaration as many times as the declared name occurs in the body of the let-expression:

                                                                                                                                                                                         LOOKUP_FOUND -----------------------------------------------------------
                                                                                                                                                                                                      (identity_2 : bool -> bool), . |- identity_2 : bool -> bool
LOOKUP_FOUND ------------------------------------------------------------------------------------    INT --------------------------------------------------------------------    LOOKUP_NOT_FOUND_YET --------------------------------------------------------------------------------------    BOOL ------------------------------------------------------------------------
             (identity_1 : int -> int), (identity_2 : bool -> bool), . |- identity_1 : int -> int        (identity_1 : int -> int), (identity_2 : bool -> bool), . |- 1 : int                         (identity_1 : int -> int), (identity_2 : bool -> bool), . |- identity_2 : bool -> bool         (identity_1 : int -> int), (identity_2 : bool -> bool), . |- true : bool
         APP ----------------------------------------------------------------------------------------------------------------------------------------------------------------                     APP -----------------------------------------------------------------------------------------------------------------------------------------------------------------------
             (identity_1 : int -> int), (identity_2 : bool -> bool), . |- identity_1 1 : int                                                                                                          (identity_1 : int -> int), (identity_2 : bool -> bool), . |- identity_2 true : bool
        PAIR ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
             (identity_1 : int -> int), (identity_2 : bool -> bool), . |- (identity_1 1, identity_2 true) : int * bool
         LET ------------------------------------------------------------------------------------------------------------
             . |- let identity_1 = fun x -> x and identity_2 = fun x -> x in (identity_1 1, identity_2 true) : int * bool

Exercise 24

Revisit Exercise 23 in the light of the postlude.

Version

Added the template .ml file [19 Mar 2023]

Edited the hint about Exercise 19 [03 Feb 2023]

Expanded Exercise 00 [02 Feb 2023]

Created [02 Sep 2022]