Induction and recursion over natural numbers¶
The goal of this lecture note is to articulate the inductive specification of a computation over natural numbers and how to program the corresponding recursive functions in OCaml.
Resources¶
- The OCaml code for the present lecture note (latest version: 12 Feb 2023).
Warning
Caveat: succ denotes a predeclared function in OCaml, it is not a data constructor for integers.
(Reminder: succ and pred respectively denote increment and decrement functions, i.e., functions that respectively add 1 and subtract 1 to their argument.)
From inductive data to structurally recursive functions¶
The concept of grammar in linguistics can be exported to specifying not just programming languages, but any kind of data. For example, here is yet again the grammar of natural numbers (Peano numbers):
<natural-number> ::= 0
| succ <natural-number>
An onion by any other name...—Juliet
This grammar is sound in that using the two constructors 0 and succ, we can construct natural numbers. And it is complete in that any natural number can be expressed as a combination of 0 and succ.
To wit:
# succ;;
- : int -> int = <fun>
# succ 0;;
- : int = 1
# succ 1;;
- : int = 2
# succ (succ 0);;
- : int = 2
#
This self-referential way of specifying data inductively has a computational counterpart: a way of processing data recursively that lets us define a self-referential, i.e., recursive, OCaml function. In the induction step, the function calls itself. Its name is then part of its definition, and it is declared with the keyword rec.
Local declaration of a recursive function¶
- <expression> ::= ... | let rec <formal> = fun <formal> -> <expression> in <expression>
The corresponding typing rule reads as follows, where G stands for <type_environment>, f and x1 stand for <formal>, e0 and e2 stand for <expression>, and t0, t1, and t2 stand for <type>:
| REC | (f : t1 -> t2), G |- fun x1 -> e2 : t1 -> t2 | (f : t1 -> t2), G |- e0 : t0 | |
| G |- let rec f = fun x1 -> e2 in e0 : t0 | |||
In words,
- in any type environment G, the expression let rec f = fun x1 -> e2 in e0 has type t0 whenever, in an extension of this environment where f has type t1 -> t2, (1) fun x1 -> e2 has type t1 -> t2 and (2) e0 has type t0.
Furthermore,
to evaluate let rec f = fun x1 -> e2 in e0,
we first evaluate the definiens, i.e., fun x1 -> e2, in an extension of the current environment where f denotes the result of evaluating fun x1 -> e2 in this extended environment; it is this self-reference that enables the recursive definition of f;
evaluating let rec f = fun x1 -> e2 in e0 then reduces to evaluating e0 in this extended environment;
the binding of f is local: it vanishes once e0 is evaluated.
Vocabulary:
- x, fun x1 -> e2, and e0 are often referred to as the formal parameter, the definiens, and the body of let rec f = fun x1 -> x2 in e0, respectively.
What would happen if we omitted rec in let rec ...?
Removing the rec would make the REC rule devolve into an instance of the LET rule where the definiens is a function abstraction:
LET G |- fun x1 -> e2 : t1 -> t2 (f : t1 -> t2), G |- e0 : t0 G |- let f = fun x1 -> e2 in e0 : t0 In the LET rule, f is only lexically visible in e0. In the REC rule, f is also lexically visible in fun x1 -> e2, which enables recursive calls in e2.
Expanding the left premise of the REC rule illustrates how e2 is processed in an environment where f is bound:
(x1 : t1), (f : t1 -> t2), G |- e2 : t2 FUN -------------------------------------------- (f : t1 -> t2), G |- fun x1 -> e2 : t1 -> t2
Forgetting to write rec, when declaring a function, means that an occurrence of the name in the body of the function lexically refers to an earlier occurrence of this name in the environment, if there was one, as per Exercise 09 in Week 04:
# let foo = fun n -> 10 + n in let foo = fun m -> foo m in foo 1;; - : int = 11 #Operationally,
- evaluating foo 1 reduces to applying the function denoted by foo to 1; this function is the result of evaluating fun m -> foo m in an environment where foo denotes the result of evaluating fun n -> 10 + n in the global environment;
- applying this function to 1 reduces to evaluating the body of fun m -> foo m, i.e., foo m, in an environment where m denotes 1 and foo denotes the function that results from evaluating fun n -> 10 + n in the global environment;
- evaluating foo m in this environment reduces to applying the function denoted by foo to 1;
- applying this function reduces to evaluating the body of fun n -> 10 + n, i.e., 10 + n, in an extension of the global environment where n denotes 1;
- evaluating 10 + n in this extended environment yields 11.
Graphically:
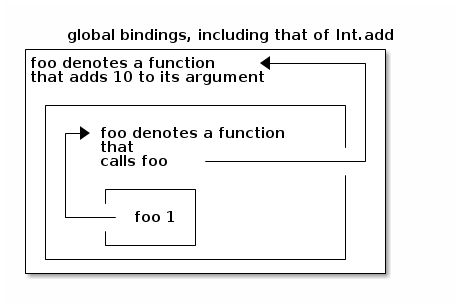
In words:
- The expression foo 1 is evaluated in an environment where foo denotes a function that calls the outer occurrence of foo.
- The expression let foo = fun m -> foo m in foo 1 is evaluated in an environment where foo denotes a function that adds 10 to its argument.
- The expression let foo = fun n -> 10 + n in let foo = fun m -> foo m in foo 1 is evaluated in the global environment.
In contrast, declaring the inner occurrence of foo with rec means that an occurrence of foo in the body of the function denoted by foo refers to this function, not to the earlier occurrence of foo in the environment.
Graphically:
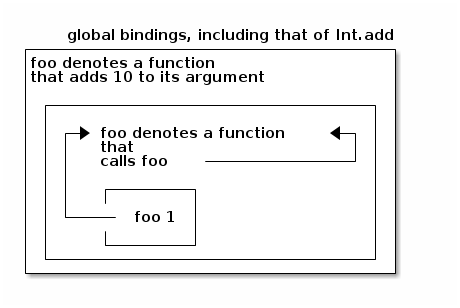
In words:
- The expression foo 1 is evaluated in an environment where foo denotes a function that calls itself. (The recursive declaration of foo shadows the outer occurrence of foo, which becomes unused.)
- The expression let rec foo = fun m -> foo m in foo 1 is evaluated in an environment where foo denotes a function that adds 10 to its argument.
- The expression let foo = fun n -> 10 + n in let rec foo = fun m -> foo m in foo 1 is evaluated in the global environment.
Operationally,
- evaluating foo 1 reduces to applying the recursive function denoted by foo to 1;
- applying this recursive function to 1 reduces to evaluating the body of fun m -> foo m, i.e., foo m, in an environment where foo denotes the recursive function and m denotes 1;
- evaluating foo m in this environment reduces to applying the recursive function denoted by foo to 1;
- applying this recursive function to 1 reduces to evaluating the body of fun m -> foo m, i.e., foo m, in an environment where foo denotes the recursive function and m denotes 1;
- evaluating foo m in this environment reduces to applying the recursive function denoted by foo to 1;
- applying this recursive function to 1 reduces to evaluating the body of fun m -> foo m, i.e., foo m, in an environment where foo denotes the recursive function and m denotes 1;
- evaluating foo m in this environment reduces to applying the recursive function denoted by foo to 1;
- ...
In other words, the evaluation of foo 1 does not terminate, after OCaml’s gentle warning that the outer occurrence of foo is not used:
# let foo = fun n -> 10 + n in let rec foo = fun m -> foo m in foo 1;; Characters 4-7: let foo = fun n -> 10 + n ^^^ Warning 26: unused variable foo.Non-termination is the computational content of the paradox induced by self-reference.
Since the show must go on, we interrupt OCaml with C-c C-c:
C-c C-cInterrupted. #
Exercise 07¶
Draw the proof tree for:
let foo = fun n -> 10 + n in let foo = fun m -> foo m in foo 1
Draw the proof tree for:
let foo = fun n -> 10 + n in let rec foo = fun m -> foo m in foo 1
Compare and contrast these two proof trees.
Global declaration of a recursive function¶
Recursive functions can also be declared at the toplevel:
- <toplevel-expression> ::= <expression> | let <formal> = <definiens> | let rec <name> = fun <formal> -> <expression>
Syntactic sugar for declaring recursive functions¶
In practice, the long-handed declaration:
let rec foo = fun x -> ...
is shortened to:
let rec foo x = ...
A first example: doubling up a natural number¶
The goal of this section is to specify the multiplication of a natural number by 2 by mathematical induction, and to then implement this computation with a recursive function.
First thing first, let us write a unit-test function:
let test_twice candidate =
let b0 = (candidate 0 = 0)
and b1 = (candidate 1 = 2)
and b2 = (candidate 2 = 4)
and b3 = (candidate 3 = 6)
and b4 = (let n = Random.int 10000
in candidate n = 2 * n)
(* etc. *)
in b0 && b1 && b2 && b3 && b4;;
For the sake of sanity, let us test this unit-test function:
# test_twice (fun n -> 2 * n) = true;; - : bool = true # test_twice (fun n -> n + n) = true;; - : bool = true # test_twice (fun n -> 2 * n + 1) = false;; - : bool = true #
For the sake of lucidity, let us implement a fake twice function that passes the unit test:
# test_twice (fun n -> if n < 10000 then 2 * n else ~-1) = true;; - : bool = true #
And let us verify that it is fake:
# (fun n -> if n < 10000 then 2 * n else ~-1) 10000 <> 10001;; - : bool = true #
Now for the idea. By the completeness of Peano numbers, the number n can be represented by applying succ n times to 0. If we were to duplicate each occurrence of succ in n, we would double n. To illustrate, let us enumerate the beginning of the graph of the doubling function:
# ( 0, 0);;
- : int * int = (0, 0)
# ( succ 0, succ (succ 0));;
- : int * int = (1, 2)
# ( succ (succ 0), succ (succ (succ (succ 0))));;
- : int * int = (2, 4)
# (succ (succ (succ 0)), succ (succ (succ (succ (succ (succ 0))))));;
- : int * int = (3, 6)
#
Hence the following inductive specification of how to double up a natural number:
- base case (n = 0): doubling up 0 yields 0
- induction step (n = succ n’): given a number n' such that doubling it yields ih (which is the induction hypothesis), doubling succ n' should yield succ (succ ih)
(To say it again, the intuition behind this inductive specification is that 2 * n = succ (succ (succ (succ (... (succ (succ (0)))...)))), where succ is iteratively applied 2 * n times to 0, as per Exercise 01.i in the lecture note about strings.)
Let us express this inductive specification as the declaration of a recursive function:
let rec twice_v0 n =
if n = 0
then ...
else let n' = pred n
in let ih = twice_v0 n'
in ...;;
In this implementation, we distinguish the base case and the induction step with an if-expression testing whether the given number is 0 or not. If it is, we put in the consequent what is specified in the base case:
let rec twice_v0 n =
if n = 0
then 0
else let n' = pred n
in let ih = twice_v0 n'
in ...;;
If the given number n is not 0, this means that it is the successor of another number, n', which we compute. We then implement the induction hypothesis with a recursive call over n', and then complete the alternative with what is specified in the induction step:
let rec twice_v0 n =
if n = 0
then 0
else let n' = pred n
in let ih = twice_v0 n'
in succ (succ ih);;
This implementation passes the unit test:
# test_twice twice_v0;;
- : bool = true
#
It also is vulnerable to being applied to a negative integer (which would make it diverge), so we should shield it by asserting that its given integer lies above 0:
let twice_v1 n =
let () = assert (n >= 0) in
let rec visit i =
if i = 0
then 0
else let i' = pred i
in let ih = visit i'
in succ (succ ih)
in visit n;;
This shielded implementation passes the unit test:
# test_twice twice_v1;;
- : bool = true
#
Because this recursive implementation mirrors the corresponding inductive specification, it is said to be structurally recursive.
That twice_v1 has type int -> int is proved by constructing the following proof tree (using the obvious typing rule GREATER_OR_EQUAL):
LOOKUP_FOUND ----------------------------------------------------------------- INT -----------------------------------------------------------------
(n : int), (succ : int -> int), (pred : int -> int), G |- n : int (n : int), (succ : int -> int), (pred : int -> int), G |- 0 : int
GREATER_OR_EQUAL ------------------------------------------------------------------------------------------------------------------------------------------
(n : int), (succ : int -> int), (pred : int -> int), G |- n >= 0 : bool
ASSERT ---------------------------------------------------------------------------------------
(n : int), (succ : int -> int), (pred : int -> int), G |- assert (n >= 0) : unit XXX
LET ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
(n : int), (succ : int -> int), (pred : int -> int), G |- let () = assert (n >= 0) in let rec visit i = if i = 0 then 0 else let i' = pred i in let ih = visit i' in succ (succ ih) in visit n : int
FUN ---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
(succ : int -> int), (pred : int -> int), G |- fun n -> let () = assert (n >= 0) in let rec visit i = if i = 0 then 0 else let i' = pred i in let ih = visit i' in succ (succ ih) in visit n : int -> int
where the tree XXX reads as follows:
LOOKUP_FOUND -----------------------------------------------------------------
(n : int), (succ : int -> int), (pred : int -> int), G |- n : int
LOOKUP_FOUND -------------------------------------------------------------------------------------------------- LOOKUP_NOT_FOUND ---------------------------------------------------------------------------------------
(visit : int -> int), (n : int), (succ : int -> int), (pred : int -> int), G |- visit : int -> int (visit : int -> int), (n : int), (succ : int -> int), (pred : int -> int), G |- n : int
APP --------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
YYY (visit : int -> int), (n : int), (succ : int -> int), (pred : int -> int), G |- visit n : int
REC ------------------------------------------------------------------------------------------------------------------------------------------------------------------------
(n : int), (succ : int -> int), (pred : int -> int), G |- let rec visit i = if i = 0 then 0 else let i' = pred i in let ih = visit i' in succ (succ ih) in visit n : int
where the tree YYY reads as follows, writing ... to stand for (n : int), (visit : int -> int), (n : int), (succ : int -> int), (pred : int -> int), G:
... |- i = 0 : bool ... |- 0 : int ... |- let i' = pred i in let ih = visit i' in succ (succ ih) : int
IF ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------
(i : int), (visit : int -> int), (n : int), (succ : int -> int), (pred : int -> int), G |- if i = 0 then 0 else let i' = pred i in let ih = visit i' in succ (succ ih) : int
FUN ---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
(visit : int -> int), (n : int), (succ : int -> int), (pred : int -> int), G |- fun i -> if i = 0 then 0 else let i' = pred i in let ih = visit i' in succ (succ ih) : int -> int
The instance of the IF typing rule features 3 premises, one for the test (i = 0), one for the consequent (0), and one for the alternative (let i' = ...). Constructing the proof trees rooted in these premises is routine.
To visualize the computation, let us instrument the implementation with tracing information. The idea is that every call to visit emits a trace, and that so does every return:
let indent indentation =
String.make (2 * indentation) ' ';;
let traced_twice_v1 n =
let () = Printf.printf "twice_v1 %s ->\n" (show_int n) in
let () = assert (n >= 0) in
let rec visit i indentation =
let () = Printf.printf "%svisit %s ->\n" (indent indentation) (show_int i) in
let result = if i = 0
then 0
else let i' = pred i
in let ih = visit i' (indentation + 1)
in succ (succ ih)
in let () = Printf.printf "%svisit %s <- %s\n" (indent indentation) (show_int i) (show_int result) in
result
in let result = visit n 1
in let () = Printf.printf "twice_v1 %s <- %s\n" (show_int n) (show_int result) in
result;;
Pablito: Huh, am I supposed to understand everything in this traced definition?Mimer: Not at first reading.
Specifically,
- initially, when traced_twice_v1 is called on a given number n, it emits the trace twice_v1 n ->,
- when traced_twice_v1 returns a final result result, it emits the trace twice_v1 n <- result,
- when visit is called on a number i, it emits the trace visit i ->, and
- when visit returns an intermediate result result, it emits the trace visit i <- result.
In addition,
- each call is indented proportionally to its nesting, and
- each return has the same indentation as the corresponding call.
To wit:
# traced_twice_v1 0;;
twice_v1 0 ->
visit 0 ->
visit 0 <- 0
twice_v1 0 <- 0
- : int = 0
# traced_twice_v1 1;;
twice_v1 1 ->
visit 1 ->
visit 0 ->
visit 0 <- 0
visit 1 <- 2
twice_v1 1 <- 2
- : int = 2
# traced_twice_v1 2;;
twice_v1 2 ->
visit 2 ->
visit 1 ->
visit 0 ->
visit 0 <- 0
visit 1 <- 2
visit 2 <- 4
twice_v1 2 <- 4
- : int = 4
# traced_twice_v1 3;;
twice_v1 3 ->
visit 3 ->
visit 2 ->
visit 1 ->
visit 0 ->
visit 0 <- 0
visit 1 <- 2
visit 2 <- 4
visit 3 <- 6
twice_v1 3 <- 6
- : int = 6
# traced_twice_v1 4;;
twice_v1 4 ->
visit 4 ->
visit 3 ->
visit 2 ->
visit 1 ->
visit 0 ->
visit 0 <- 0
visit 1 <- 2
visit 2 <- 4
visit 3 <- 6
visit 4 <- 8
twice_v1 4 <- 8
- : int = 8
# traced_twice_v1 5;;
twice_v1 5 ->
visit 5 ->
visit 4 ->
visit 3 ->
visit 2 ->
visit 1 ->
visit 0 ->
visit 0 <- 0
visit 1 <- 2
visit 2 <- 4
visit 3 <- 6
visit 4 <- 8
visit 5 <- 10
twice_v1 5 <- 10
- : int = 10
#
Food for thought¶
The implementation of the traced version of twice_v1 starts with:
let traced_twice_v1 n =
let () = Printf.printf "twice_v1 %s ->\n" (show_int n) in
let () = assert (n >= 0) in
...
Would it be equivalent to first test whether the given argument is non-negative? That is to say:
let traced_twice_v1 n =
let () = assert (n >= 0) in
let () = Printf.printf "twice_v1 %s ->\n" (show_int n) in
...
- If the two versions are equivalent, why is that?
- If the two versions are not equivalent, is one to be preferred over the other? Why?
Simplifying the definition of the doubling function¶
In the induction step, the let-expressions are said to be linear, in that the name they declare is used exactly once. Furthermore this name is used immediately. Therefore these let-expressions are only cosmetic and we can unfold them, i.e., substitute their definiens for the name they declare. Let us proceed step by step:
unfolding the declaration of n':
let twice_v2 n = let () = assert (n >= 0) in let rec visit i = if i = 0 then 0 else let ih = visit (pred i) in succ (succ ih) in visit n;;We have substituted the definiens pred i for the name i'.
unfolding the declaration of ih:
let twice_v3 n = let () = assert (n >= 0) in let rec visit i = if i = 0 then 0 else succ (succ (visit (pred i))) in visit n;;We have substituted the definiens visit (pred i) for the name ih.
Both simplified implementations pass the unit test:
# test_twice twice_v2;;
- : bool = true
# test_twice twice_v3;;
- : bool = true
#
Exercise 08¶
The goal of this exercise is to implement the addition function for natural numbers in OCaml. By the completeness of Peano numbers, the first number x can be represented by applying succ x times to 0. If we were to prepend these applications of succ to the second number y, we would add x to y. To illustrate, let us enumerate the beginning of the graph of the addition function when the second number is 10:
# (( 0, 10), 10);;
- : (int * int) * int = ((0, 10), 10)
# (( succ 0, 10), succ 10);;
- : (int * int) * int = ((1, 10), 11)
# (( succ (succ 0), 10) succ (succ 10));;
- : (int * int) * int = ((2, 10), 12)
# (( succ (succ (succ 0)), 10), succ (succ (succ 10)));;
- : (int * int) * int = ((3, 10), 13)
# ((succ (succ (succ (succ 0))), 10), succ (succ (succ (succ 10))));;
- : (int * int) * int = ((4, 10), 14)
#
Hence the following inductive specification of how to add two natural numbers. Given a second natural number y,
- base case (i = 0): adding 0 to y yields y
- induction step (i = succ i’): given a number i' such that adding it to y yields ih (which is the induction hypothesis), adding succ i' to y should yield succ ih
(To say it again, the intuition behind this inductive specification is that x + y = succ (succ (succ (... (succ y)...))), where 1 is iteratively added x times to y, as per Exercise 01.k in the lecture note about strings.)
To this end,
write a unit-test function:
let test_add a = ...
define a structurally recursive function that embodies the inductive specification above (and that uses succ):
let add_v0 x y = ...
Does your recursive function pass your unit test?
can you shield your definition so that it handles being applied to a negative integer as its first argument?
ever the helpful ones, Anton and Alfrothul proposed the following definition:
let add_v1 x y = x - (0 - y);;
Does this proposed definition pass your unit test?
Solution for Exercise 08¶
add is specified over natural numbers, i.e., non-negative integers, so let’s try a few:
let test_add a = (* an instance of the base case: *) let b0 = (let y = Random.int 2000 in a 0 y = y) (* a random instance of the induction step: *) and b1 = (let y = Random.int 2000 and i' = Random.int 1000 in a (succ i') y = succ (a i' y)) (* a few handpicked numbers: *) and b2 = (a 0 100 = 100) and b3 = (a 1 100 = 101) and b4 = (a 2 100 = 102) (* using a witness implementation of the addition function *) and b5 = (let x = Random.int 1000 and y = Random.int 2000 in a x y = x + y) (* etc. *) in b0 && b1 && b2 && b3 && b4 && b5;;For the sake of sanity, let us test this unit-test function:
# test_add (+) = true;; - : bool = true # test_add (-) = false;; - : bool = true #
For the sake of lucidity, let us implement a fake addition function that passes the unit test:
# test_add (fun x y -> if x < 1000 then x + y else ~-1) = true;; - : bool = true #
And let us verify that it is fake:
# (fun x y -> if x < 1000 then x + y else ~-1) 1000 0 <> 1000;; - : bool = true #
since add is specified over natural numbers, we might as well shield it. Here is its skeleton:
let add_v0 x y = let () = assert (x >= 0) in let rec visit i = if i = 0 then ... else let i' = pred i in let ih = visit i' in ... ih ... in visit x;;Rationale:
- the assert-expression ensures that the first argument is not a negative integer (the expressions not (x < 0), x >= 0, and 0 <= x are all equivalent);
- the skeleton of the recursive function named visit embodies the base case (i denotes 0) and the induction step (i denotes the successor of an integer i’).
Now all we need is to fill the blanks:
in the base case, the result is y, and
in the induction step, the result is obtained by applying succ to the result of the recursive call:
let add_v0 x y = let () = assert (x >= 0) in let rec visit i = if i = 0 then y else let i' = pred i in let ih = visit i' in succ ih in visit x;;
This shielded implementation is structurally recursive and it passes our unit test:
# test_add add_v0;; - : bool = true #
Not only that, but since it is structurally recursive, code coverage is ensured since the unit-test function tests both the base case and the induction step.
our definition is already shielded.
yes, Anton and Alfrothul’s definition passes our unit test:
# test_add add_v1;; - : bool = true #
This definition is mathematically correct because subtracting a negative number is the same as adding the corresponding positive number.
To visualize the recursive computation implemented in add_v0, let us instrument this implementation with tracing information:
let traced_add_v0 x y =
let () = Printf.printf "add_v0 %s %s ->\n" (show_int x) (show_int y) in
let () = assert (x >= 0) in
let rec visit i indentation =
let () = Printf.printf "%svisit %s ->\n" (indent indentation) (show_int i) in
let result = if i = 0
then y
else let i' = pred i
in let ih = visit i' (indentation + 1)
in succ ih
in let () = Printf.printf "%svisit %s <- %s\n" (indent indentation) (show_int i) (show_int result) in
result
in let result = visit x 1
in let () = Printf.printf "add_v0 %s %s <- %s\n" (show_int x) (show_int y) (show_int result) in
result;;
Specifically,
- initially, when traced_add_v0 is called with a given x and a given y, it emits the trace add_v0 x y ->,
- when traced_add_v0 returns a final result result, it emits the trace add_v0 x y <- result,
- when visit is called on a number i, it emits the trace visit i ->, and
- when visit returns an intermediate result result, it emits the trace visit i <- result.
In addition,
- each call is indented proportionally to its nesting, and
- each return has the same indentation as the corresponding call.
To wit:
# traced_add_v0 0 10;;
add_v0 0 10 ->
visit 0 ->
visit 0 <- 10
add_v0 0 10 <- 10
- : int = 10
# traced_add_v0 1 10;;
add_v0 1 10 ->
visit 1 ->
visit 0 ->
visit 0 <- 10
visit 1 <- 11
add_v0 1 10 <- 11
- : int = 11
# traced_add_v0 2 10;;
add_v0 2 10 ->
visit 2 ->
visit 1 ->
visit 0 ->
visit 0 <- 10
visit 1 <- 11
visit 2 <- 12
add_v0 2 10 <- 12
- : int = 12
# traced_add_v0 3 10;;
add_v0 3 10 ->
visit 3 ->
visit 2 ->
visit 1 ->
visit 0 ->
visit 0 <- 10
visit 1 <- 11
visit 2 <- 12
visit 3 <- 13
add_v0 3 10 <- 13
- : int = 13
#
In the induction step, the let-expressions that declare i' and ih, in the definition of visit, are cosmetic and so we can unfold them:
let add_v2 x y =
let () = assert (x >= 0) in
let rec visit i =
if i = 0
then y
else succ (visit (pred i))
in visit x;;
This simplified implementation is still structurally recursive and it passes the unit test:
# test_add add_v2;;
- : bool = true
#
Interlude¶
Pablito: The exercise was about adding two natural numbers, right?
Mimer: Yes it was.
Pablito: And since OCaml does not have natural numbers, but only integers, we have put an assertion to check that the function is not applied to a negative integer, right?
Mimer: Right.
Pablito: Then why is the implementation only checking that the first argument is non-negative and not the second?
Mimer: Good point, Pablito. Do you think it matters?
Pablito: Addition is commutative?
Mimer: Yup.
Exercise 09¶
Consider the following OCaml function:
let following n =
let () = assert (n >= 0) in
let rec visit i =
if i = 0
then n
else let i' = pred i
in let ih = visit i'
in succ ih
in visit n;;
Which mathematical function does this OCaml function compute? Why is that?
Exercise 10¶
The goal of this exercise is to implement the multiplication function for natural numbers in OCaml. By the completeness of Peano numbers, the first number x can be represented by applying succ x times to 0. If we were to replace each occurrence of succ with the addition of y, we would multiply x and y. To illustrate, let us enumerate the beginning of the graph of the multiplication function when the second number is 10:
# (( 0, 10), 0);;
- : (int * int) * int = ((0, 10), 0)
# (( succ 0, 10), 10 + 0);;
- : (int * int) * int = ((1, 10), 10)
# (( succ (succ 0), 10), 10 + (10 + 0));;
- : (int * int) * int = ((2, 10), 20)
# (( succ (succ (succ 0)), 10), 10 + (10 + (10 + 0)));;
- : (int * int) * int = ((3, 10), 30)
# ((succ (succ (succ (succ 0))), 10), 10 + (10 + (10 + (10 + 0))));;
- : (int * int) * int = ((4, 10), 40)
#
Hence the following inductive specification of how to multiply two natural numbers. Given a second natural number y,
- base case (i = 0): multiplying 0 and y yields 0
- induction step (i = succ i’): given a number i' such that multiplying it to y yields ih (which is the induction hypothesis), multiplying succ i' and y should yield y + ih
(To say it again, the intuition behind this inductive specification is that x * y = y + (... (y + (y + (y + (0))))...), where y is iteratively added to the left x times to 0, as per Exercise 01.j in the lecture note about strings.)
This inductive specification is aligned with the other inductive specifications so far (i.e., for computing a Factorial number, for doubling up a natural number, and for adding two natural numbers), but for the sake of variation, and since addition is commutative, let us consider the following alternative inductive specification. Given an integer y,
- base case (i = 0): multiplying 0 and y yields 0
- induction step (i = succ i’): given a number i' such that multiplying it to y yields ih (which is the induction hypothesis), multiplying succ i' and y should yield ih + y
(To say it again, the intuition behind this inductive specification is that x * y = (...((((0) + y) + y) + y) ...) + y, where y is iteratively added to the right x times to 0, as per Exercise 01.m in the lecture note about strings.)
To this end,
write a unit-test function:
let test_mul m = ...
define a structurally recursive function that embodies the inductive specification above (and that uses add_v0 or add_v1):
let mul_v0 x y = ...
Does your recursive function pass your unit test?
ever the helpful ones, Anton and Alfrothul proposed the following definition:
let mul_v1 x y = x / (1 / y);;
Does this proposed function pass your unit test?
Solution for Exercise 10¶
mul is specified over natural numbers, i.e., non-negative integers, so let’s try a few:
let test_mul m = (* an instance of the base case: *) let b0 = (let y = Random.int 1000 in m 0 y = 0) (* a random instance of the induction step: *) and b1 = (let y = Random.int 1000 and i' = Random.int 99 in m (succ i') y = (m i' y) + y) (* a few handpicked numbers: *) and b2 = (m 0 100 = 0) and b3 = (m 1 100 = 100) and b4 = (m 2 100 = 200) (* using a witness implementation of the multiplication function *) and b5 = (let x = Random.int 100 and y = Random.int 1000 in m x y = x * y) (* etc. *) in b0 && b1 && b2 && b3 && b4 && b5;;For the sake of sanity, let us test this unit-test function:
# test_mul ( * ) = true;; - : bool = true # test_mul ( + ) = false;; - : bool = true #
For the sake of lucidity, let us implement a fake multiplication function that passes the unit test:
# test_mul (fun x y -> if x < 200 then x * y else ~-1) = true;; - : bool = true #
And let us verify that it is fake:
# (fun x y -> if x < 200 then x * y else ~-1) 200 0 <> 0;; - : bool = true # (fun x y -> if x < 200 then x * y else ~-1) 200 1 <> 200;; - : bool = true #
since mul is specified over natural numbers, we might as well shield it. Here is its skeleton:
let mul_v0 x y = let () = assert (x >= 0) in let rec visit i = if i = 0 then ... else let i' = pred i in let ih = visit i' in ... in visit x;;Rationale:
- the assert-expression ensures that the first argument is not a negative integer;
- the skeleton of the recursive function named visit embodies the base case (i denotes 0) and the induction step (i denotes the successor of an integer i’).
Now all we need is to fill the blanks:
in the base case, the result is 0, and
in the induction step, the result is obtained by applying add_v0 to the result of the recursive call and to y:
let mul_v0 x y = let () = assert (x >= 0) in let rec visit i = if i = 0 then 0 else let i' = pred i in let ih = visit i' in add_v0 ih y in visit x;;
This shielded implementation is structurally recursive and it passes our unit test:
# test_mul mul_v0;; - : bool = true #
Also, since it is structurally recursive, code coverage is ensured since the unit-test function tests both the base case and the induction step.
our definition is already shielded.
no, Anton and Alfrothul’s definition does not pass our unit test:
# test_mul mul_v1;; Exception: Division_by_zero. #
This definition only works when the second argument is 1 because / computes the quotient function.
To visualize the computation, let us instrument the implementation with tracing information. The idea is that every call to visit emits a trace, and that so does every return:
let traced_mul_v0 x y =
let () = Printf.printf "mul_v0 %s %s ->\n" (show_int x) (show_int y) in
let () = assert (x >= 0) in
let rec visit i indentation =
let () = Printf.printf "%svisit %s ->\n" (indent indentation) (show_int i) in
let result = if i = 0
then 0
else let i' = pred i
in let ih = visit i' (indentation + 1)
in ih + y
in let () = Printf.printf "%svisit %s <- %s\n" (indent indentation) (show_int i) (show_int result) in
result
in let result = visit x 1
in let () = Printf.printf "mul_v0 %s %s <- %s\n" (show_int x) (show_int y) (show_int result) in
result;;
Specifically,
- initially, when traced_mul_v0 is called with a given x and a given y, it emits the trace mul_v0 x y ->,
- when traced_mul_v0 returns a final result result, it emits the trace mul_v0 x y <- result,
- when visit is called on a number i, it emits the trace visit i ->, and
- when visit returns an intermediate result result, it emits the trace visit i <- result.
In addition,
- each call is indented proportionally to its nesting, and
- each return has the same indentation as the corresponding call.
To wit:
# traced_mul_v0 0 10;;
mul_v0 0 10 ->
visit 0 ->
visit 0 <- 0
mul_v0 0 10 <- 0
- : int = 0
# traced_mul_v0 1 10;;
mul_v0 1 10 ->
visit 1 ->
visit 0 ->
visit 0 <- 0
visit 1 <- 10
mul_v0 1 10 <- 10
- : int = 10
# traced_mul_v0 2 10;;
mul_v0 2 10 ->
visit 2 ->
visit 1 ->
visit 0 ->
visit 0 <- 0
visit 1 <- 10
visit 2 <- 20
mul_v0 2 10 <- 20
- : int = 20
# traced_mul_v0 3 10;;
mul_v0 3 10 ->
visit 3 ->
visit 2 ->
visit 1 ->
visit 0 ->
visit 0 <- 0
visit 1 <- 10
visit 2 <- 20
visit 3 <- 30
mul_v0 3 10 <- 30
- : int = 30
#
In the induction step, the let-expressions that declare n' and ih, in the definition of visit, are cosmetic and so we can unfold them:
let mul_v2 x y =
let () = assert (x >= 0) in
let rec visit i =
if i = 0
then 0
else add_v0 (visit (pred i)) y
in visit x;;
This simplified implementation is still structurally recursive and it passes the unit test:
# test_mul mul_v2;;
- : bool = true
#
Aftermath¶
Anton: Did you notice how the traced version of mul_v0 is using + instead of add_v0, in the induction step?
Alfrothul: True. And I didn’t notice. But it shouldn’t make any difference, should it?
Anton: Well, I don’t know. Suppose that it uses traced_add_v0.
Alfrothul: Oh, right – we could then see how each induction step in the multiplication function triggers an addition:
let traced_mul_v0' x y =
let () = Printf.printf "mul_v0' %s %s ->\n" (show_int x) (show_int y) in
let () = assert (x >= 0) in
let rec visit i indentation =
let () = Printf.printf "%svisit %s ->\n" (indent indentation) (show_int i) in
let result = if i = 0
then 0
else let i' = pred i
in let ih = visit i' (indentation + 1)
in traced_add_v0 ih y
in let () = Printf.printf "%svisit %s <- %s\n" (indent indentation) (show_int i) (show_int result) in
result
in let result = visit x 1
in let () = Printf.printf "mul_v0 %s %s <- %s\n" (show_int x) (show_int y) (show_int result) in
result;;
Anton: Let’s see:
# traced_mul_v0' 2 3;;
mul_v0' 2 3 ->
visit 2 ->
visit 1 ->
visit 0 ->
visit 0 <- 0
add_v0 0 3 ->
visit 0 ->
visit 0 <- 3
add_v0 0 3 <- 3
visit 1 <- 3
add_v0 3 3 ->
visit 3 ->
visit 2 ->
visit 1 ->
visit 0 ->
visit 0 <- 3
visit 1 <- 4
visit 2 <- 5
visit 3 <- 6
add_v0 3 3 <- 6
visit 2 <- 6
mul_v0 2 3 <- 6
- : int = 6
#
Alfrothul: That seems broken.
Anton: Yes, the indentation is off, for example.
Alfrothul: Right – because traced_add_v0 assumes it is called at the toplevel, but it isn’t.
Anton: Also, it is confusing that both traced_mul_v0 and traced_add_v0 use visit as a trace.
Alfrothul: So we should define another version of traced_add_v0 that is parameterized by the current number of nested calls.
Dana (interjecting): Ditto for traced_mul_v0' in case it is not called at the toplevel.
Anton: And we should make traced_mul_v0 and traced_add_v0 use distinct instances of visit as a trace:
let traced_add_v0' x y given_indentation =
let () = Printf.printf "%sadd_v0 %s %s ->\n" (indent given_indentation) (show_int x) (show_int y) in
let () = assert (x >= 0) in
let rec visit i indentation =
let () = Printf.printf "%svisit_add_v0 %s ->\n" (indent indentation) (show_int i) in
let result = if i = 0
then y
else let i' = pred i
in let ih = visit i' (indentation + 1)
in succ ih
in let () = Printf.printf "%svisit_add_v0 %s <- %s\n" (indent indentation) (show_int i) (show_int result) in
result
in let result = visit x (given_indentation + 1)
in let () = Printf.printf "%sadd_v0 %s %s <- %s\n" (indent given_indentation) (show_int x) (show_int y) (show_int result) in
result;;
let traced_mul_v0' x y =
let () = Printf.printf "mul_v0' %s %s ->\n" (show_int x) (show_int y) in
let () = assert (x >= 0) in
let rec visit i indentation =
let () = Printf.printf "%svisit %s ->\n" (indent indentation) (show_int i) in
let result = if i = 0
then 0
else let i' = pred i
in let ih = visit i' (indentation + 1)
in traced_add_v0 ih y
in let () = Printf.printf "%svisit %s <- %s\n" (indent indentation) (show_int i) (show_int result) in
result
in let result = visit x 1
in let () = Printf.printf "mul_v0 %s %s <- %s\n" (show_int x) (show_int y) (show_int result) in
result;;
Alfrothul: Let’s see:
# traced_mul_v0' 2 3;;
- : int -> int = <fun>
#
Anton: Huh?
Alfrothul: My bad. As Dana pointed out, we need to tell traced_mul_v0' that it starts with zero nested calls:
# traced_mul_v0' 4 2 0;;
mul_v0 4 2 ->
visit_mul_v0 4 ->
visit_mul_v0 3 ->
visit_mul_v0 2 ->
visit_mul_v0 1 ->
visit_mul_v0 0 ->
visit_mul_v0 0 <- 0
add_v0 0 2 ->
visit_add_v0 0 ->
visit_add_v0 0 <- 2
add_v0 0 2 <- 2
visit_mul_v0 1 <- 2
add_v0 2 2 ->
visit_add_v0 2 ->
visit_add_v0 1 ->
visit_add_v0 0 ->
visit_add_v0 0 <- 2
visit_add_v0 1 <- 3
visit_add_v0 2 <- 4
add_v0 2 2 <- 4
visit_mul_v0 2 <- 4
add_v0 4 2 ->
visit_add_v0 4 ->
visit_add_v0 3 ->
visit_add_v0 2 ->
visit_add_v0 1 ->
visit_add_v0 0 ->
visit_add_v0 0 <- 2
visit_add_v0 1 <- 3
visit_add_v0 2 <- 4
visit_add_v0 3 <- 5
visit_add_v0 4 <- 6
add_v0 4 2 <- 6
visit_mul_v0 3 <- 6
add_v0 6 2 ->
visit_add_v0 6 ->
visit_add_v0 5 ->
visit_add_v0 4 ->
visit_add_v0 3 ->
visit_add_v0 2 ->
visit_add_v0 1 ->
visit_add_v0 0 ->
visit_add_v0 0 <- 2
visit_add_v0 1 <- 3
visit_add_v0 2 <- 4
visit_add_v0 3 <- 5
visit_add_v0 4 <- 6
visit_add_v0 5 <- 7
visit_add_v0 6 <- 8
add_v0 6 2 <- 8
visit_mul_v0 4 <- 8
mul_v0 4 2 <- 8
- : int = 8
#
Anton: Wow.
Alfrothul: Actually, more like “Yay” – the trace clearly shows the series of additions triggered by recursive calls in the multiplication function.
Pablito: Er... Doesn’t this series grows as the computation proceeds?
Alfrothul: Beg pardon?
Anton: Well spotted, Pablito – visit_mul_v0 successively returns 0, and then 2, and then 4, etc., and each time, it triggers a call to add_v0 with this number and the multiplicand.
Pablito: The multiplicand?
Loki: Well, you know, as the French say, culture is like marmalade: the less you have of it, the more you spread it.
Halcyon: Like, “marmalade” is “confiture” in French, which rhymes with “culture”.
Pablito (clickety-clickety-click): I see. The first argument of the multiplication function is the multiplier and the second the multiplicand.
Anton: Right. In infix form, the left operand is the multiplier and the right one the multiplicand.
Pablito: Still, the first argument of add_v0 is growing, and so the bigger the multiplier, the more additions, no?
Dana (jumping in): Good point, Pablito. Multiplying succ x and y entails succ x additions, just as adding a and b entails a calls to succ. So multiplying succ x and y entails 0 + y + 2 * y + 3 * y + ... + x * y calls to succ.
Alfrothul: In other words, factoring y on the right, (0 + 1 + 2 + 3 + ... + x) * y calls to succ.
Anton: Or again (Gauss to the rescue), (x * (x + 1) / 2) * y calls to succ.
Dana: In short, a number of calls to succ that is proportional to the product of the square of x and of y.
Anton: Which is not too good.
Alfrothul: Which is why we should rather use the built-in addition function instead of add_v0, I guess. Surely it is implemented more efficiently.
Anton: By that token, we should simply use the built-in multiplication function instead of mul_v0, and then what would we learn?
Pablito: Maybe we should just swap the arguments of add_v0?
Anton (o_o): Swap the arguments of add_v0.
Pablito: Well, yes, in the definition of the traced multiplication function:
let traced_mul_v0'' x y given_indentation =
let () = Printf.printf "%smul_v0 %s %s ->\n" (indent given_indentation) (show_int x) (show_int y) in
let () = assert (x >= 0) in
let rec visit i indentation =
let () = Printf.printf "%svisit_mul_v0 %s ->\n" (indent indentation) (show_int i) in
let result = if i = 0
then 0
else let i' = pred i
in let ih = visit i' (indentation + 1)
in traced_add_v0' y ih (indentation + 1) (* <--- here *)
in let () = Printf.printf "%svisit_mul_v0 %s <- %s\n" (indent indentation) (show_int i) (show_int result) in
result
in let result = visit x (given_indentation + 1)
in let () = Printf.printf "%smul_v0 %s %s <- %s\n" (indent given_indentation) (show_int x) (show_int y) (show_int result) in
result;;
After all, addition is commutative.
Pablito (to Mimer): And now it matters that the multiplicand is non-negative.
Alfrothul (pragmatic): Let me see:
# traced_mul_v0'' 5 2 0;;
mul_v0 5 2 ->
visit_mul_v0 5 ->
visit_mul_v0 4 ->
visit_mul_v0 3 ->
visit_mul_v0 2 ->
visit_mul_v0 1 ->
visit_mul_v0 0 ->
visit_mul_v0 0 <- 0
add_v0 2 0 ->
visit_add_v0 2 ->
visit_add_v0 1 ->
visit_add_v0 0 ->
visit_add_v0 0 <- 0
visit_add_v0 1 <- 1
visit_add_v0 2 <- 2
add_v0 2 0 <- 2
visit_mul_v0 1 <- 2
add_v0 2 2 ->
visit_add_v0 2 ->
visit_add_v0 1 ->
visit_add_v0 0 ->
visit_add_v0 0 <- 2
visit_add_v0 1 <- 3
visit_add_v0 2 <- 4
add_v0 2 2 <- 4
visit_mul_v0 2 <- 4
add_v0 2 4 ->
visit_add_v0 2 ->
visit_add_v0 1 ->
visit_add_v0 0 ->
visit_add_v0 0 <- 4
visit_add_v0 1 <- 5
visit_add_v0 2 <- 6
add_v0 2 4 <- 6
visit_mul_v0 3 <- 6
add_v0 2 6 ->
visit_add_v0 2 ->
visit_add_v0 1 ->
visit_add_v0 0 ->
visit_add_v0 0 <- 6
visit_add_v0 1 <- 7
visit_add_v0 2 <- 8
add_v0 2 6 <- 8
visit_mul_v0 4 <- 8
add_v0 2 8 ->
visit_add_v0 2 ->
visit_add_v0 1 ->
visit_add_v0 0 ->
visit_add_v0 0 <- 8
visit_add_v0 1 <- 9
visit_add_v0 2 <- 10
add_v0 2 8 <- 10
visit_mul_v0 5 <- 10
mul_v0 5 2 <- 10
- : int = 10
#
Pablito: See? Now the first argument of add_v0 doesn’t grow.
Dana: Well done, Pablito. Now multiplying succ x and y entails 0 + y + y + y + ... + y, i.e., x * y calls to succ.
Pablito: So, a number of calls to succ that is proportional to x * y instead of to x * x * y. That seems more natural since we are computing the product of x and y.
Anton: So all in all, we should write:
let mul_v3 x y =
let () = assert (x >= 0) in
let rec visit i =
if i = 0
then 0
else add_v0 y (visit (pred i))
in visit x;;
Alfrothul: Or we could just use the built-in addition function:
let mul_v4 x y =
let () = assert (x >= 0) in
let rec visit i =
if i = 0
then 0
else visit (pred i) + y
in visit x;;
let mul_v5 x y =
let () = assert (x >= 0) in
let rec visit i =
if i = 0
then 0
else y + visit (pred i)
in visit x;;
And then whether we write y + visit (pred x) or visit (pred x) + y doesn’t matter.
Pablito: All these definitions pass the unit test, but running the one for mul_v2 is perceptibly slower:
# test_mul mul_v5;;
- : bool = true
# test_mul mul_v4;;
- : bool = true
# test_mul mul_v3;;
- : bool = true
# test_mul mul_v2;;
- : bool = true
#
Loki: Plus, we can now call each of traced_mul_v0'' and traced_add_v0' with a negative indentation. That could come handy.
Dana: A fire in the sky.
Loki: I knew you loved this guitar riff too.
Exercise 11¶
The goal of this exercise is to implement the exponentiation function for natural numbers in OCaml. By the completeness of Peano numbers, the exponent n can be represented by applying succ n times to 0. If we were to map each occurrence of succ by the multiplication of the base x, we would exponentiate x with n. To illustrate, let us enumerate the beginning of the graph of the exponentiation function when the first number is 10:
# ((10, 1), 10);;
- : (int * int) * int = ((10, 1), 10)
# ((10, 2), 10 * 10);;
- : (int * int) * int = ((10, 2), 100)
# ((10, 3), 10 * 10 * 10);;
- : (int * int) * int = ((10, 3), 1000)
# ((10, 4), 10 * 10 * 10 * 10);;
- : (int * int) * int = ((10, 4), 10000)
#
So the induction step is clear:
- induction step (i = succ i’): given a number i’ such that exponentiating x with i’ yields ih (which is the induction hypothesis), exponentiating x with succ i' should yield x * ih
But what about the base case? In other words, what about exponentiating x with 0?
By continuity, we should align this base case with the induction step: since the operation in the induction step is a multiplication, let us use the neutral element of multiplication in the base case:
- base case (i = 0): exponentiating x with 0 yields 1
Revising the enumeration of the beginning of the graph of the exponentiation function when the first number is 10:
# ((10, 0), 1);;
- : (int * int) * int = ((10, 0), 1)
# ((10, 1), 10 * 1);;
- : (int * int) * int = ((10, 1), 10)
# ((10, 2), 10 * (10 * 1));;
- : (int * int) * int = ((10, 2), 100)
# ((10, 3), 10 * (10 * (10 * 1)));;
- : (int * int) * int = ((10, 3), 1000)
# ((10, 4), 10 * (10 * (10 * (10 * 1))));;
- : (int * int) * int = ((10, 4), 10000)
#
Algebraically, using the neutral element of multiplication in the base case makes sense because of the law:
x^(m + n) = x^m * x^n
If, e.g., the first summand is 0, this law reads:
x^(0 + n) = x^0 * x^n
which simplifies to:
x^n = x^0 * x^n
which compels the equality:
x^0 = 1
Ditto for the law:
x^(m * n) = (x^m)^n
(For simplicity, we posit that exponentiating 0 with 0 yields 1.)
All told, here is the inductive specification of how to exponentiate a natural number with another. Given a first natural number x,
- base case (i = 0): exponentiating x with 0 yields 1
- induction step (i = succ i’): given a number i’ such that exponentiating x with i’ yields ih (which is the induction hypothesis), exponentiating x with succ i' should yield x * ih
(To say it again, the intuition behind this inductive specification is that x^n = x * (x * (...(x * 1)...)), where x is iteratively multiplied n times, starting with 1, as per Exercise 01.l in the lecture note about strings.)
Here is a quick and dirty unit-test function:
let test_power p =
(* a few handpicked numbers: *)
let b0 = (p 2 0 = 1)
and b1 = (p 2 1 = 2)
and b2 = (p 2 2 = 4)
and b3 = (p 2 3 = 8)
and b4 = (p 2 4 = 16)
and b5 = (p 2 5 = 32)
and b6 = (p 10 2 = 100)
(* etc. *)
in b0 && b1 && b2 && b3 && b4 && b5 && b6;;
Questions:
Expand and test test_power with an instance of the base case and a random instance of the induction step, as in Section Using random numbers to test the factorial function.
You might be tempted to use OCaml’s predefined exponentiation function over floats ( ** ) (together with the conversion functions int_of_float and float_of_int) as a witness implementation, but then beware of its approximations, for they can make unit tests fail unduly – in other words, using ( ** ) is not necessarily a good idea here. There is no need to try to dance faster than the music.
Define a structurally recursive function that embodies the inductive specification above (and that uses mul_v0, mul_v2, or mul_v3):
let power_v0 x n = ...
Does your recursive function pass your unit test? Does your unit-test function provide code coverage?
Can you shield your definition so that it handles being applied to a negative integer as its second argument?
It would be great if you could instrument your implementation with tracing information.
For efficiency, you should use the native multiplication, not your implementation of it, especially if it uses your implementation of addition. Why is that? Can you quantify the computational steps taken by your implementation?
Food for thought:
Alternatively to positing that exponentiating 0 with 0 yields 1, we can keep this case undefined in the implementation:
let power x n =
let () = assert (not (x = 0 && n = 0) && n >= 0) in
...
Then this case should not be considered in the unit tests, just like the case of negative exponents is not considered.
Exercise 12¶
In the inductive specification of the factorial function, the induction step, namely:
(n + 1)! = (n + 1) * n!
is simple to justify, since:
(n + 1)! = (n + 1) * n * (n - 1) * ... * 3 * 2 * 1
n! = n * (n - 1) * ... * 3 * 2 * 1
But what about the base case? Namely:
0! = 1
Hint: read the statement of Exercise 11.
The even predicate¶
The goal of this section is to write a predicate (i.e., a function that returns a Boolean) computing whether a given natural number is even. Let us start with a unit-test function:
let test_evenp candidate =
(* testing the soundness of the even predicate with a few handpicked numbers: *)
let b0 = (candidate 0 = true)
and b1 = (candidate 1 = false)
and b2 = (candidate 2 = true)
and b3 = (candidate 3 = false)
and b4 = (candidate 4 = true)
and b5 = (candidate 5 = false)
and b6 = (candidate 1000 = true)
and b7 = (candidate 1001 = false)
(* testing the completeness of the even predicate with a few random numbers: *)
and b8 = (let n = Random.int 1000
in candidate (2 * n) = true)
and b9 = (let n = Random.int 1000
in candidate (2 * n + 1) = false)
(* etc. *)
in b0 && b1 && b2 && b3 && b4 && b5 && b6 && b7 && b8 && b9;;
For the sake of sanity, let us test this unit-test function:
# test_evenp (fun n -> n mod 2 = 0) = true;; - : bool = true # test_evenp (fun n -> n mod 2 = 1) = false;; - : bool = true #
For the sake of lucidity, let us implement a fake predicate that passes the unit test:
# test_evenp (fun n -> if n < 2001 then n mod 2 = 0 else false) = true;; - : bool = true #
And let us verify that it is fake:
# (fun n -> if n < 2001 then n mod 2 = 0 else false) 2002 <> true;; - : bool = true #
Now for the idea. The successor of an even number is odd, i.e., not even, and the successor of an odd number is even. In other words, the evenness of the successor of a number is the negation of the evenness of this number.
Hence the inductive specification of how to test whether a natural number is even:
- base case (i = 0): 0 is even
- induction step (i = succ i’): given a number i' such that its evenness is the Boolean ih (which is the induction hypothesis), the evenness of succ i' is not ih
The unit-test function already contains an instance of the base case, but let us expand it with a random instance of the induction step:
let test_evenp candidate =
(* testing the soundness of the even predicate with a few handpicked numbers: *)
let b1 = (candidate 1 = false)
and b2 = (candidate 2 = true)
and b3 = (candidate 3 = false)
and b4 = (candidate 4 = true)
and b5 = (candidate 5 = false)
and b6 = (candidate 1000 = true)
and b7 = (candidate 1001 = false)
(* testing the completeness of the even predicate with a few random numbers: *)
and b8 = (let n = Random.int 1000
in candidate (2 * n) = true)
and b9 = (let n = Random.int 1000
in candidate (2 * n + 1) = false)
(* an instance of the base case: *)
and bc = (candidate 0 = true)
(* a random instance of the induction step: *)
and is = (let i' = Random.int 1000
in candidate (succ i') = not (candidate i'))
(* etc. *)
in b1 && b2 && b3 && b4 && b5 && b6 && b7 && b8 && b9 && bc && is;;
Let us express this inductive specification as the declaration of a recursive function:
let evenp_v0 n =
let () = assert (n >= 0) in
let rec visit i =
if i = 0
then ...
else let i' = pred i
in let ih = visit i'
in ...
in visit n;;
In the base case, visit should yield true and in the induction step, visit (succ i') should yield the negation of the induction hypothesis:
let evenp_v0 n =
let () = assert (n >= 0) in
let rec visit i =
if i = 0
then true
else let i' = pred i
in let ih = visit i'
in not ih
in visit n;;
This implementation is structurally recursive and it passes the unit test, which provides code coverage since it tests both the base case and the induction step:
# test_evenp evenp_v0;;
- : bool = true
#
In the induction step, the let-expressions that declare i' and ih, in the definition of visit, are cosmetic and so we can unfold them:
let evenp_v1 n =
let () = assert (n >= 0) in
let rec visit i =
if i = 0
then true
else not (visit (pred i))
in visit n;;
This simplified implementation is still structurally recursive and it passes the unit test:
# test_evenp evenp_v1;;
- : bool = true
#
The accompanying resource file contains a traced version of evenp_v0:
# traced_evenp_v0 5;;
evenp_v0 5 ->
visit 5 ->
visit 4 ->
visit 3 ->
visit 2 ->
visit 1 ->
visit 0 ->
visit 0 <- true
visit 1 <- false
visit 2 <- true
visit 3 <- false
visit 4 <- true
visit 5 <- false
evenp_v0 5 <- false
- : bool = false
# traced_evenp_v0 4;;
evenp_v0 4 ->
visit 4 ->
visit 3 ->
visit 2 ->
visit 1 ->
visit 0 ->
visit 0 <- true
visit 1 <- false
visit 2 <- true
visit 3 <- false
visit 4 <- true
evenp_v0 4 <- true
- : bool = true
#
The odd predicate¶
The goal of this section is to write a predicate computing whether a given natural number is odd.
Exercise 13¶
Along the lines of the previous section, specify, implement, and test the oddp predicate.
After hours¶
Pablito (falling asleep): Weird stuff, this multiplier and this multiplicand. I wonder if a similar weird stuff happens for addition. Could be funny...
Pablito’s dream¶
And then the Lord said: go forth, you multipliers and multiplicands, and multiply. And the throng of animals, big and small, scampered away to do just that, except two tiny ones who stayed there, looking up at Him in dismay.
The Lord (kindly): Yes?
The two tiny animals (in dismay): But we can’t multiply – we’re adders.
So the Lord took his mighty axe and chopped down a tree (material cause: wood, and efficient cause: the Lord himself), swiftly assembled a contraption (formal cause), and presented it to them along with its final cause:
The Lord (majestically): Here is a table of logs. Now go forth and multiply.
Resources¶
- The OCaml code for the present lecture note (latest version: 12 Feb 2023).
Version¶
Added illustrations that the fake functions are fake [19 Mar 2023]
Stated that the instance of the induction step is random in test_add, test_mul, test_power, and test_evenp [04 Mar 2023]
Added a pointer to Wikipedia about exponentiating 0 with 0 yields 1 [21 Feb 2023]
Added a traced version of following in the accompanying .ml file for Exercise 09 [12 Feb 2023]
Added Exercise 12 [12 Feb 2023]
Added the enumeration of the graphs for the doubling function, the addition function, the multiplication function, and the exponentiation function [11 Feb 2023]
Quantified the variables in the type-inference rules [23 Jan 2023]
Created [09 Sep 2022]